Меридиан, проходящий через центр главного зала Гринвичской обсерватории; Гринвич – округ г. Лондона

- 15 -

Геодезической широтой B точки K называется угол KОB, который образует нормаль KC' с плоскостью экватора.

Геодезической долготой L точки K называется двугранный угол, образованный плоскостями геодезических меридианов данной точки и начального. Плоскостью геодезического меридиана данной точки называется плоскость, содержащая нормаль к поверхности эллипсоида в этой точке и полярную ось PP'. Сечение поверхности эллипсоида этой плоскостью называется геодезическим меридианом. Геодезические меридианы – эллипсы. Сечения поверх-ности эллипсоида плоскостями, перпендикулярными полярной оси - геодезические параллели. Геодезические параллели - окружности. Счет и название геодезических широт аналогичен астрономическим. Счет геодезических долгот ведется от гринвичского меридиана на восток от 0 до 360^º. Положение точки на поверхности земного эллипсоида вполне определяется геодезическими координатами: геодезической широтой Bи геодезической долготой L. Для определения положения точки A, находящейся на физической поверхности Земли, необходимо знать третью величину – высоту (см. рис. 2.11,б и 2.12).

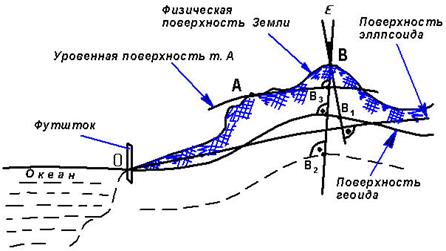
Рис. 2.12. Высоты точек

-16 -

Высоты различают: абсолютные – H = BB₁, условные - H' = BB₂ и относительные (превышения) – h = BB₃ . Абсолютной высотой точки земной поверхности называется расстояние ее до основной уровенной поверхности Земли, измеренное по нормали к поверхности эллипсоида. В России и странах СНГ в качестве основной уровенной поверхности принята поверхность, совпадающая со средним уровнем воды Финского залива Балтийского моря. Счет абсолютных высот ведется от ноля Кронштадского футштока*. Система абсолютных высот называется Балтийской. Условной высотой точки земной поверхности называется расстояние этой точки до уровенной поверхности, не совпадающей с основной, измеренное по отвесной линии в данной точке. Превышениемh(относительной высотой) точки B над точкой A называется расстояние точки B до уровенной поверхности точки A, измеренное по нормали к этой поверхности. Геодезические измерения по определению высот точек земной поверхности называются нивелированием. Численное выражение высоты точки называетсявысотной отметкойили, просто,отметкой.

2.4.4. Влияние кривизны Земли на определение высот точек

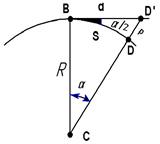При замене небольшого участка BD (рис. 2.13) уровенной поверх-ности Земли касательной BD' точка D перемещается в D', в связи с чем меняется ее высота на величину p. Величина p выражает влияние кривизны Земли на высоты

точек и называется поправкой за кривизну Земли. Определим ее величину. Из прямоугольного треугольника CBD' имеем

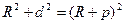. (2.8)

Далее получим 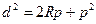, (2.9)

Откуда 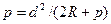. (2.10)

Так как p весьма мало по сравнению

с R, то в знаменателе правой части

равенства его можно отбросить. Рис. 2.13. Поправка

за кривизну Земли

Он представляет собой медную пластину, замурованную в один из устоев моста обводного канала в Кронштадте; нанесенная на пластину черта является нулем футштока. Название образовалось путем соединения английского слова foot (фут) с немецким stock (палка, шест).

- 17 -

Тогда окончательно получим 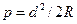. (2.11)

Легко подсчитать, что при d = 1 км и R = 6371 км, p = 78,5 мм, а при d = 100 м, p = 0,8 мм. Следует иметь что высоты точек местно-сти часто необходимо знать с точностью до 1,0 мм. Поэтому, даже при коротких расстояниях (50 ÷ 100 м), влияние кривизны Земли на высоты точек необходимо учитывать.

2.4.5. Проекция Гаусса – Крюгера*. Зональная и условная

системы прямоугольных координат на плоскости.

В СССР с 1928 г. для составления топографических карт приме-няется равноугольная (конформная) поперечно-цилиндрическая проекция, предложенная К.Ф. Гауссом. Сущность проекции Гаусса состоит в следующем. Представим, что земной шар вписан в цилиндр (см. рис. 2.14), который касается его по среднему (осевому) меридиану зоны POР'. Ось цилиндра HH' расположена в плоскости экватора Q'OQ и проходит через центр C шара. Плоское изображение каждой зоны получают путём проектирования ее определенным образом на боковую поверхность цилиндра, касающегося осевого меридиана зоны. После чего цилиндр раз-резается по образующей KK' и его боковая поверхность раз-вёртывается в плоскость. При проектировании зоны Гаусс поставил условие, чтобы изображение малого участка на цилиндре было подобно соответствующему участку на сфере; следовательно, углы между соответствующими линиями на шаре и на плоскости равны между собой.

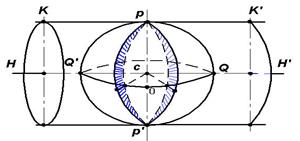
Рис. 2.14. К проекции Гаусса - Крюгера

Проекция разработана Гауссом в 30-х годах XIX в.; в 1912 г. Крюгер в работе " Конформное изображение земного эллипсоида на плоскости" предложил формулы для вычисления в этой проекции.

- 18 -

Выполнение этого условия приводит к увеличению длин линий на плоскости. Величину искажения ∆s линий проекции можно вычислить по формуле 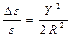, (2.12)

где 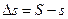; s - длина линии на шаре; S - длина проекции линии;

Y - расстояние от осевого меридиана зоны до средней точки линии; R - радиус земного шара (R = 6371,11 км ).

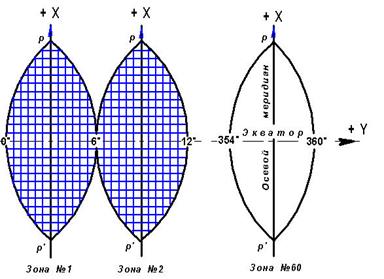
Рис. 2.15. Проекции зон

Для территории СНГ на широтах 36 ≤ φ ≤ 70^° , величина линейного искажения на краях зоны меняется от 1 / 1100 до 1/ 6000. Такие величины не превышают графических погрешностей построения карт масштаба 1:10 000, поэтому масштаб изображения на таких и более мелкого масштаба картах в проекции Гаусса остается постоянным. Для планов масштабов 1:5000 и крупнее применяются трехградусные зоны. Счет зон ведется от Гринвичского меридиана на восток. Проектируя последовательно одну зону за другой, получают изображение поверхности земного шара в виде шестидесяти плоских двуугольников (рис. 2.15).

- 19 -

2.4.6. Зональная система плоских прямоугольных координат

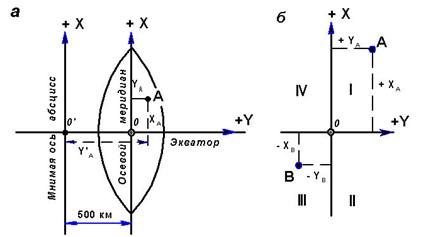Данная система образуется двумя взаимно перпендикулярными линиями, представляющими изображения осевого меридиана зоны и экватора на плоскости. Изображение осевого меридиана принимается за ось абсцисс с положительным направлением на север. Осью ординат является изображение экватора с положительным направлением на восток.

Рис. 2.16. Системы прямоугольных координат

Для территории СНГ, расположенной в северном полушарии, абсциссы любых точек положительны. Чтобы сделать положительными и ординаты точек, условились перенести начало счета ординат к западу от осевого меридиана на 500 км (см. рис. 2.16). Эти ординаты называются преобразованными. Номер зоны, к которой относятся координаты, указывается перед численным значением преобразованной ординаты. Например, точка с координатами X = 6015,76 и Y = 9652,66 км находится в зоне №9 на расстоянии 152,66 км к востоку от осевого меридиана этой зоны.

2.4.7. Условная система прямоугольных координат на плоскости

Для инженерно-геодезических работ, выполняемых на небольших площадях, применяют условную систему прямоугольных координат (рис. 2.16, б).

- 20 -

Ось абсцисс (оX) такой системы совмещают с меридианом некоторой (обычно крайней юго-западной) точки участка, либо располагают параллельно основным осям сооружений. Положительное направление оси абсцисс (oX) выбирают на север (на чертеже - вверх), оси ординат (oY) - на восток (на чертеже - вправо). Применяемая в геодезии система прямоугольных координат называется левой. В ней поворот от оси oX к оси oY (на наименьший угол) до их совмещения осуществляется по движению часовой стрелки.