КООРДИНАТ, ПРИМЕНЯЕМЫХ В ГЕОДЕЗИИ
2.1. Отвесная линия и уровенная поверхность
Геодезические измерения, выполняемые в любой точке физической поверхности Земли, связаны с направлением отвесной линии в этой точке. Например, при измерении горизонтального угла теодолитом, ось вращения его совмещают с отвесной линией, проходящей через вершину угла. Геометрическое нивелирование выполняют горизонтальным лучом визирования, т.е. перпендикулярным отвесной линии в точке установки нивелира. Измеренное расстояние между точками местности проектируют на горизонтальную плоскость при помощи отвесных линий в этих точках. Простейший прибор - отвеспоказывает направление действия силы тяжести Земли; подвешенный на нити груз под действием силы тяжести натягивает нить, которая и указывает направление отвесной линии в данной точке. Из курса физики известно, что сила тяжести G есть равнодействующая двух сил: силы притяжения ЗемлиF и центробежной силы P (рис. 2.1).
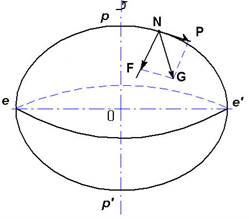
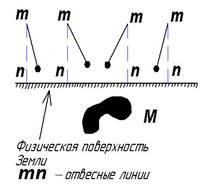
Рис. 2.1. К понятию о силе Рис. 2.2. Направления силы
тяжести Земли тяжести Земли
- 6 -
Вектор силы F направлен приблизительно к центру Земли. Наи-большее значение силаF имеет на полюсах и наименьшее – на экваторе. Сила Pимеет максимальное значение на экваторе, где она составляет приблизительно 1:288 от величины F. На полюсах сила P равна нулю. Следовательно, сила G на земной поверхности непрерывно увеличивается от экватора к полюсам и на полюсах имеет максимальное значение. В свою очередь сила земного притяженияF есть равнодействующая притяжений всех масс, заключенных в теле Земли. Значит, величина и направление силы обусловлены распределением этих масс. Отсюда следует, что и направление отвесной линии тоже зависит от распределения масс в теле Земли.
Из курса физики известно, что в гравитационном поле Земли работа силы тяжести не зависит от формы пути MN (рис. 2.3), а зависит только от положения начальной и конечной точек этого пути. Поле, обладающее таким свойством, называется потенциальным. Во всяком потенциальном поле можно провести так называемые уровенныеповерхности, т.е. такие поверхности, при движении материальной точки по которым сила поля работы не совершает. Нетрудно доказать, что в гравитационном поле Земли расстояние между уровенными поверхностями убывает к полюсам.
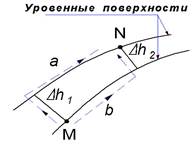
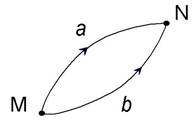
Рис. 2.3. К понятию о Рис. 2.4. Непараллельность
работе силы тяжести уровенных поверхностей
- 7 -
Возьмём две точки M и N в плоскости земного меридиана, лежа-щие на разных, но близких одна к другой, уровенных поверхностях (рис. 2.4). Согласно сказанному выше о работе силы тяжести, можем написать выражения для работы по пути MaNи по пути MbN и приравнять их: 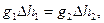
где ∆h1 и ∆h2 - расстояния между уровенными поверхностями,
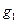 и
и 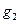 - величины ускорений силы тяжести в точкахM и N.
- величины ускорений силы тяжести в точкахM и N.
 Сила тяжести G возрастает к полюсам, следовательно,
Сила тяжести G возрастает к полюсам, следовательно, 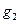 >
> 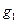 . Поэтому из равенства легко увидеть, что
. Поэтому из равенства легко увидеть, что 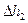 <
< 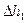 . Вывод: уровенные поверхности гравитационного поля Земли между собой непараллельны и расстояние между ними уменьшается к полюсам.
. Вывод: уровенные поверхности гравитационного поля Земли между собой непараллельны и расстояние между ними уменьшается к полюсам.
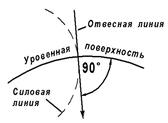
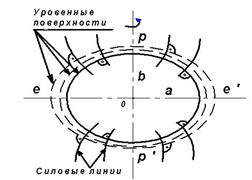
Рис. 2.5. Уровенные поверхности Рис. 2.6. Направление
и силовые линии гравитационного отвесной линии
поля Земли
Линии, нормальные к уровенным поверхностям, называются силовыми линиями (см. рис. 2.5). Касательная к силовой линии в данной точке есть отвесная линия в этой точке. Следовательно, отвесная линия является нормалью к уровенной поверхности (рис. 2.6). Поверхность воды в спокойном состоянии является одной из уровенных поверхностей. Можно провести бесчисленное множество уровенных поверхностей; каждая из них вблизи земной поверхности будет поверхностью неразрывной, замкнутой, без складок и рёбер. Вид уровенной поверхности зависит от распределения масс в теле Земли.
- 8 -
При равномерном распределении масс (см. рис. 2.7) эта поверхность будет занимать положение, показанное пунктиром. При наличии массы M с преувеличенной плотностью уровенная поверхность будет иметь некоторый выгиб кверху.
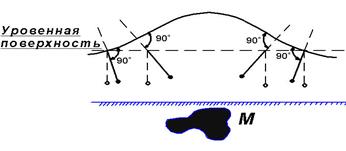
Рис. 2.7. Вид уровенной поверхности
2.2. Основная уровенная поверхность. Геоид. Эллипсоид.
Как отмечалось выше, геодезические измерения связаны с направлением отвесной линии в тех точках, в которых они выполнялись. Значит, в каждой такой точке результаты измерений могут быть отнесены именно к той уровенной поверхности, которая проходит через данную точку. Но в таком случае результаты измерений на пунктах какой-либо геодезической сети окажутся отнесенными к различным уровенным поверхностям и замкнутых фигур в сети не образуется. В связи с этим возникает необходимость приведения результатов всех геодезических измерений прежде всего к некоторой данной или принятой в качестве общей исходной уровенной поверхности. В качестве основной уровенной поверхности Земли принята поверхность вод морей и океанов в их невозмущенном (спокойном) состоянии, мысленно продолженная под материками таким образом, что в любой ее точке она нормальна (перпендикулярна) отвесной линии в этой точке.
Тело, ограниченное основной уровенной поверхностью, называют геоидом.Вследствие неравномерного распределения масс внутри Земли поверхность геоида является весьма сложной и не выражается ни одной из рассматриваемых в математике поверхностей. Поэтому возникла необходимость замены поверхности геоида вспомогательной, возможно ближе подходящей к ней поверхности.
- 9 -
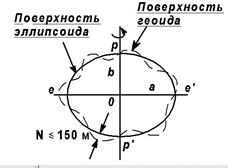
В первом приближении уровенную поверхность Земли можно заменить сферой определенного радиуса. Но, наиболее близкой к геоиду является фигура, образованная вращением эллипса pe'p'e (рис. 2.8) вокруг малой оси pp', называемой полярной осью. В связи с этим возникает необходимость в определении размеров земного эллипсоида, т.е. в определении его параметров: большой полуоси a, малой полуоси b, сжатия 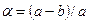 и данных, определяющих положение эллипсоида относительно геоида. Эллипсоид, наиболее близко подходящий к фигуре геоида в целом,
и данных, определяющих положение эллипсоида относительно геоида. Эллипсоид, наиболее близко подходящий к фигуре геоида в целом,  называется общим земным эллипсоидом.
называется общим земным эллипсоидом.
 Эллипсоид, c определенными
Эллипсоид, c определенными
параметрами, ориентирован-
ный в теле Земли и принятый для производства всех карто-графо - геодезических работ
в данной стране, называется референц - эллипсоидом.
В России для производства картографо - геодезических работ принят эллипсоид, определение размеров кото-рого и ориентирование в теле
Рис. 2.8. Общий Земной эллипсоид Земли выполнены под руковод-
ством Ф.Н. Красовского.
Эллипсоид Красовского имеет слеующие размеры:
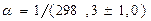 ; a =
; a = 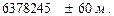
В настоящее время за фигуру Земли принимается тело, ограниченное физической поверхностью Земли, т.е.: на cуше - поверхностью ее твердой оболочки, а на территории океанов и морей - их невозмущенной поверхностью. Изучение фигуры Земли производится путем определения положения точек местности в избранной системе координат на поверхности фигуры относимости, т.е. на поверхности референц-эллипсоида Красовского. Отметим, что при решении многих задач геодезии за фигуру Земли с достаточной для практических целей точностью принимается шар, равновеликий по объёму эллипсоиду Красовского, с радиусом R =6371,11км. Для сравнительно небольших участков земной поверхности в качестве поверхности относимости можно принять горизонтальную плоскость. Горизонтальной называют плоскость, которая нормальна отвесной линии в данной точке поверхности Земли.
- 10 -
2.3. Расчёт размеров участка сферической (уровенной) поверхности Земли для обобщения её до горизонтальной плоскости
Пусть ABD (рис. 2.9) часть уровенной поверхности Земли, принимаемой за сферу с центром cи радиусом R. Обозначим длину дуги ABD через s. Проведем в средней точке B дуги ABD касательную к ней и продолжим радиусы CA и CD до пересечения с касательной в точках A' и D'. Рассчитаем, какая погрешность произойдёт от замены дуги sотрезком касательной A'D' = d. Для этого определим разность
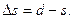 (2.1)
(2.1)
Обозначим центральный угол ACD через ε . Тогда
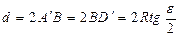 и
и 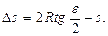 (2.2)
(2.2)
Раскладывая 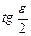 в ряд Маклорена и, ограничиваясь при этом двумя членами разложения, получим
в ряд Маклорена и, ограничиваясь при этом двумя членами разложения, получим
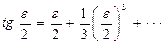 , ( 2.3)
, ( 2.3)
где ε - выражено в радианной мере. В свою очередь, как центральный угол
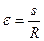 , (2.4)
, (2.4)
поэтому формула (2.3) примет вид
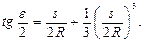 (2.5) Подставив (2.5) в (2.2), получим
(2.5) Подставив (2.5) в (2.2), получим
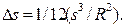 (2.6)
(2.6)
Найдём отношение погрешности Δsк s, которое в геодезии принято называть относительной погрешноcтью.
Будем иметь 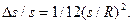 (2.7)
(2.7)
Максимальная точность линейных измерений на поверхности Земли составляет 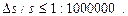 С учетом равенства (2.7)
С учетом равенства (2.7)
вычислим 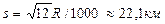 при R = 6371,11 км.
при R = 6371,11 км.
- 11 –
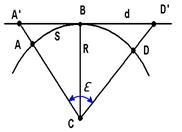
Следовательно, участок сферичес- кой поверхности Земли диаметром 22,1 км, площадью 383,6 км2, можно с практически неощутимой погрешно-стью принять за плоский, а кривизной поверхности Земли в пределах ука-занного участка можно пренебречь.
Рис. 2.9. Влияние кривизны Земли
на горизонтальные расстояния
2.4. Определение положения точек земной поверхности и применяемые для этого в геодезии системы координат
2.4.1. Метод проекций в геодезии. Величины, подлежащие измерению
Физическая поверхность Земли – сочетание различного рода пространственных форм: холмов, котловин, хребтов, лощин, балок, оврагов и т.д. Для изучения такой сложной поверхности в геодезии применяют метод проекций. Так как фигуру Земли в первом приближении принимают за шар, рассмотрим способ проектирования земной поверхности на сферу. Допустим, что поверхности геоида и эллипсоида на некотором участке совпадают, образуя одну уровенную поверхность MN (рис. 2.10,а).
Пространственный многоугольник ABCDEF физической поверхности Земли проектируют на поверхность MN отвесными линиями. Точки a, b, c, d, e, f, в которых отвесные линии пересекают уровенную поверхность MN, называют горизонтальными проекциями соответствующих точек местности, а многоугольник abcdef – горизонтальной проекцией многоугольника ABCDEF. Чтобы по горизонтальной проекции можно было судить о форме пространственного многоугольника, очевидно, необходимо знать величины Aa, Bb, Cc,...,Ff, т.е. расстояния точек местности по отвесным линиям до уровенной поверхности Земли, называемые высотами точек местности. В § 2.3 было показано, что небольшой участок сферической и уровенной поверхностей Земли можно заменить горизонтальной плоскостью, касающейся поверхности в центре этого участка.
- 12 –
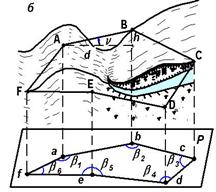
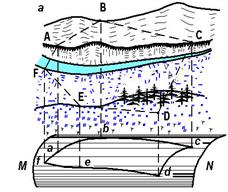
Рис. 2.10. Схемы к методу проекций
Поэтому, если участок местности, заключенный в многоугольнике ABCDEF (см. рис. 2.10,б), имеет небольшие размеры, то при проек-тировании уровенную поверхность заменяют горизонтальной плоскостью P. Линии проектирования Aa,Bb,.., и т.д. перпендику-лярны плоскости P *, стороны ab, bc,...,cf и углы между ними явля-ются горизонтальными проекциями соответствующих сторон и углов местности, а плоский многоугольник abcdef - горизонтальной проекцией многоугольника ABCDEF, расположенного на физической поверхности Земли. Непосредственными измерениями на местности получают: расстояния AB, BC,...,FA, горизонтальные углыβ1, β2, β3,…, между ними, превышения h и углы наклона ν линий. От непосредственно измеренной длины линии местности, например 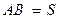 , переходят к длине ее проекции на горизонтальную плоскость
, переходят к длине ее проекции на горизонтальную плоскость 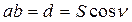 . Длина ортогональной проекции линии местности на горизонтальную плоскость называется горизонтальным проложениемэтой линии. Углом наклона (вертикальным углом) линии местности называется линейный угол в отвесной плоскости между этой линией и ее проекцией на горизонтальную плоскость. По измеренным превышениям вычисляют высоты точек местности. Например, по известной высоте Aa точки A и превышению h получим высоту
. Длина ортогональной проекции линии местности на горизонтальную плоскость называется горизонтальным проложениемэтой линии. Углом наклона (вертикальным углом) линии местности называется линейный угол в отвесной плоскости между этой линией и ее проекцией на горизонтальную плоскость. По измеренным превышениям вычисляют высоты точек местности. Например, по известной высоте Aa точки A и превышению h получим высоту 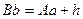 .
.
______________________
Дата добавления: 2016-01-09; просмотров: 1910;
