Термодинамика обратимых электрохимических систем

Изменение энергии Гиббса для реакции, обратимо протекающей в гальваническом элементе, можно записать

D_rG = – zFЕ. (3.46)

Запишем также уравнение Гиббса — Гельмгольца

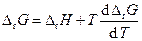. (3.47)

Тогда

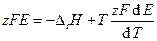. (3.48)

Учитывая, что для химической реакции справедливо

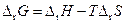. (3.49)

Получим

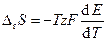. (3.50)

Таким образом, температурный коэффициент ЭДС связан с изменением энтропии химической реакции, протекающей в гальваническом элементе.

На практике, измеряя ЭДС гальванического элемента при разных температурах и постоянном давлении, мы можем определить как изменение энтропии, так и изменение энтальпии соответствующей химической реакции.

Потенциометрия

Потенциометрия — метод исследования, в основе которого лежат термодинамические соотношения между ЭДС электрохимических цепей, с одной стороны, и физико-химическими параметрами растворов и химических реакций с другой. Потенциометрию используют для определения

— pH растворов,

— констант гидролиза солей,

— констант диссоциации кислот и оснований,

— произведений растворимости малорастворимых соединений,

— констант устойчивости комплексов,

— коэффициентов активности ионов в растворах,

— термодинамических характеристик химических реакций

— и т. д.

Например, ионное равновесие в растворе характеризуется соответствующими термодинамическими константами. Например, для малорастворимого соединения, диссоциирующего по уравнению

AB 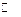A⁺ + B^–

равновесие характеризуется произведением растворимости:

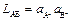. (3.51)

Для определения произведения растворимости можно составить гальванический элемент

A | AB | DB || AC | A,

где AC и DB — хорошо растворимые соли соответствующего катиона (A⁺) и аниона (B^–), A⁺ | A — электрод первого рода, а B^– | AB, A — электрод второго рода. На электродах будут протекать следующие реакции:

(1) A⁺ + e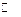^– A,

(2) AB + e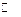^– A + B^–.

Запишем уравнения Нернста для этих электродов.

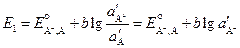, (3.52)

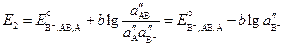. (3.53)

Электрод второго рода можно представить как электрод первого рода, только с очень малой концентрацией иона металла, которая будет зависеть от концентрации аниона, образующего с ним малорастворимое соединение. Тогда, учитывая выражение для произведения растворимости, получим

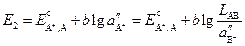. (3.54)

Выражение для ЭДС этого элемента будет

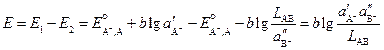. (3.55)

Таким образом, произведение растворимости малорастворимого соединения связано с ЭДС рассмотренного элемента, и для его определения необходимо измерить ЭДС элемента при известных активностях иона металла (A⁺) в растворе первого электрода и аниона B^– в растворе второго.

Для определения других термодинамических констант необходимо составлять соответствующие электрохимические цепи и измеряя их ЭДС при известных активностях потенциалопределяющих веществ вычислять значение констант.

Рассмотрим, например, как методом потенциометрии можно оценить термодинамические функции химических реакций (DG, DA, DS, DH и DU ). Для этого необходимо составить электрохимический элемент, результатом работы которого была бы исследуемая химическая реакция. По ЭДС этого гальванического элемента можно рассчитать:

1) изменение энергии Гиббса:

DG = - zFE ; (3.56)

2) изменение энергии Гельмгольца:

DA = - zFE - Dn RT, (3.57)

где Dn – изменение числа молей газообразных веществ, участвующих в реакции;

3) изменение энтропии можно оценить, зная зависимость ЭДС элемента от температуры:

DS= zF 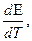(3.58)

где 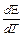– температурный коэффициент ЭДС. Величину температурного коэффициента ЭДС определяют экспериментально по графической или аналитической зависимости ЭДС элемента от температуры.

Например, зависимость ЭДС от температуры можно описать уравнением:

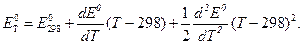(3.59)

При изменении температуры ЭДС элемента может оставаться постоянной величиной, увеличиваться или уменьшаться в зависимости от величины и знака температурного коэффициента ЭДС.

4) изменение внутренней энергии системы:

DU = Q_v = - zF (E-T 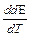) - Dn ×RT . (3.60)

5) тепловой эффект химической реакции:

DH = Q_p = - zF(E - T 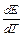). (3.61)

Если реакция в элементе протекает без выделения газов, то можно принять, что

DH = DU , (Q_p = Q_v) . (3.62)

Приведённые выше выражения можно использовать и для вычисления стандартных величин (DG° , DA°, DS°, DH°, DU°).

Если стандартные термодинамические потенциалы определяются по справочным данным, то возможно решение обратной задачи, то есть определение стандартной ЭДС. При этом используются соотношения:

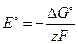, (3.63)

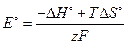, (3.64)

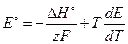. (3.65)