Концентрационные цепи
Гальванические элементы второго типа – концентрационные цепи представляют собой элементы, составленные из электродов, на которых протекают одинаковые химические реакции, но концентрации реагирующих веществ на электродах различны. Электрическая энергия в концентрационных элементах вырабатывается за счет выравнивания концентраций веществ.
Различают концентрационные цепи без переноса и с переносом. Концентрационными цепями без переноса называются элементы:
а) с одинаковыми электродами, но с разными концентрациями электролитов при отсутствии непосредственного соприкосновения между растворами;
б) с электродами из двух сплавов (амальгам), одинаковых по природе, но разных по концентрации, опущенными в один раствор электролита;
в) с газовыми электродами, одинаковыми по природе, но с разным давлением газа (с одним раствором электролита).
Примером концентрационной цепи без переноса может служить амальгамная концентрационная цепь:
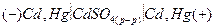
a2 a1,
где a1 и a2 – активности кадмия в амальгаме.
На электродах этого концентрационного элемента протекают следующие электрохимические реакции:
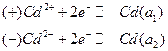 .
.
Суммарная реакция в элементе - 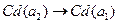 .
.
ЭДС этого элемента вырабатывается за счет выравнивания активности кадмия в амальгамах ( 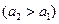 ):
):
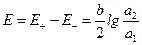 . (3.37)
. (3.37)
Концентрационными цепями с переносом называются такие концентрационные элементы, в которых имеется непосредственная граница соприкосновения между растворами. На границе между растворами двух одинаковых электролитов разной концентрации, в результате разной подвижности катионов и анионов, возникает так называемый диффузионный потенциал 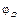
Например,
jD
Cu | CuSO4 ¦ CuSO4 | Cu
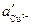 >
> 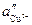
где 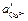 и
и 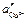 — различные активности ионов меди на электродах, jD — диффузионный потенциал, возникающий на границе растворов.
— различные активности ионов меди на электродах, jD — диффузионный потенциал, возникающий на границе растворов.
Запишем потенциалы обоих электродов:
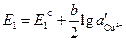 ,
,
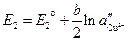 . (3.38)
. (3.38)
Тогда ЭДС элемента будет
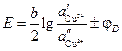 . (3.39)
. (3.39)
Как правило, различие в концентрациях веществ на разных электродах концентрационных элементов мало, поэтому диффузионный потенциал вносит существенный вклад в общую ЭДС. Существует несколько соотношений для расчета ЭДС гальванического элемента с учетом диффузионного потенциала.
1. Если электроды обратимы относительно катиона, то ЭДС гальванического элемента будет равна:
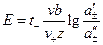 , (3.40)
, (3.40)
где t– –число переноса анионов, n – общее число формульных частиц, составляющих данный электролит (общее число ионов, на которые распадается электролит ), n+ — число формульных частиц катионов(число катионов, на которые диссоциирует электролит), составляющих данный электролит.
Диффузионный потенциал рассчитывается в этом случае по соотношению:
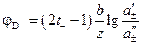 . (3.41)
. (3.41)
Примером концентрационного гальванического элемента обратимого относительно катиона будет, например, элемент:
jD
Zn | ZnSO4 ¦ ZnSO4 | Zn
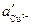 >
> 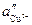
2. Если электроды обратимы относительно аниона, то ЭДС гальванического элемента будет равна:
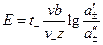 , (3.42)
, (3.42)
где t+ – число переноса катионов, n– – число формульных частиц анионов, составляющих данный электролит.
Диффузионный потенциал рассчитывается в этом случае по соотношению:
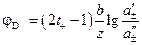 . (3.43)
. (3.43)
Примером концентрационного гальванического элемента обратимого относительно аниона будет, например, элемент:
jD
Ag | AgCl | HCl(aq) | NaCl(aq) | AgCl | Ag
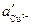 >
> 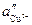
3. Так как причиной возникновения диффузионного потенциала является различная подвижность ионов, то он возникает даже на границе двух различных растворов одинаковой концентрации. В этом случае для различных бинарных электролитов 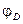 можно рассчитать по уравнению
можно рассчитать по уравнению
jD = 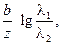
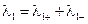 –;
–; 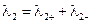 , (3.44)
, (3.44)
где 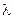 + и
+ и 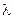 – – подвижности ионов электролита;
– – подвижности ионов электролита; 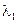 >
> 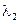 .
.
Диффузионный потенциал может быть величиной как положительной, так и отрицательной:
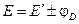 , (3.45)
, (3.45)
где 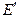 - разность потенциалов между электродами элемента, без учета
- разность потенциалов между электродами элемента, без учета 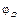 .
.
Выбор знака “+” или “–” перед диффузионным потенциалом зависит от взаимного направления электрических полей между электродами элемента и на границе двух растворов. Если направления обоих электрических полей совпадают (см. пример), то диффузионный потенциал (абсолютная величина) прибавляется к 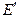 , а если направления обоих полей не совпадают, то вычитается. Например,
, а если направления обоих полей не совпадают, то вычитается. Например,
jD
(–) Ag|AgNO3(aq)–½+AgNO3 (aq)| Ag (+) ( 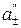 >
> 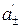 )
)
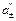
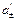
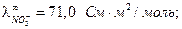
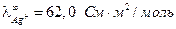 ;
; 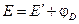 .
.
Дата добавления: 2016-01-09; просмотров: 3650;
