Определение внутренних усилий в балках
при плоском поперечном изгибе (задачи № 12–15)
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 2 (§ 2.5).
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 5 (§ 22).
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 7 (§ 7.1–7.5).
Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений из уравнений отсеченной части балки следует, что поперечную силуможно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент численно равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).
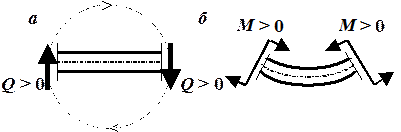 Рис. 4.5. Правило знаков: а – для поперечной силы;
б – для изгибающего момента в балке
Рис. 4.5. Правило знаков: а – для поперечной силы;
б – для изгибающего момента в балке
|
Введем правила знаков для поперечной силы и изгибающего момента. Поперечная сила считается положительной, если она обходит сечение по часовой стрелке (т. е. сила, находящаяся слева от сечения и направленная вверх, или сила, находящаяся справа от сечения и направленная вниз, – положительны) (рис. 4.5, а).Изгибающий момент положителен, если он изгибает балку выпуклостью вниз. Обращаем внимание на то, что знак внутреннего усилия – изгибающего момента – зависит от того, с какой стороны от сечения находится момент[3]. Как видно из рис. 4.5, б момент, находящийся слева от сечения, действует по часовой стрелке, а момент, расположенный справа от сечения, – против часовой стрелки. И оба они положительны.
При построении эпюр Q и М договоримся на эпюре Q положительные значения откладывать сверху нулевой линии. На эпюре М у строителей принято откладывать положительные ординаты снизу. Такое правило построения эпюры М называется построением эпюры со стороны растянутых волокон, т. е. положительные значения М откладываются в сторону выпуклости изогнутой балки.
Известно [2], что изгибающий момент М, поперечная сила и интенсивность распределенной нагрузки q связаны между собой такими дифференциальными зависимостями:
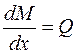 , (4.11)
, (4.11)
 (4.12)
(4.12)
и, как следствие (4.11) и (4.12),
 . (4.13)
. (4.13)
При выводе формул (4.11)–(4.13) нагрузка 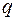 считалась положительной, если она направлена вниз.
считалась положительной, если она направлена вниз.
Из определений для поперечной силы и изгибающего момента, а также из дифференциальных зависимостей (4.11)–(4.13) вытекают следующие правила проверки правильности построения эпюр Q и М:
На эпюре Q под сосредоточенной силой имеет место скачок на величину этой силы. На эпюре М в этом сечении должен быть перелом, т. е. резкое изменение угла наклона прямой (или касательной к кривой).
На эпюре М скачок имеет место под сосредоточенной парой на величину этой пары.
Из зависимостей (4.11), (4.12) можно определить вид функций Q и М:
· если на участке отсутствует распределенная нагрузка (q = 0), то  , а М – линейная функция x;
, а М – линейная функция x;
· если на участке действует равномерно распределенная нагрузка (q = const), то Q – линейная функция, а М – квадратная парабола;
· если на участке действует линейно распределенная нагрузка, то соответственно Q является квадратной параболой, а М – кубической.
3. Характер поведения функции на участке (то есть ее возрастание или убывание) зависит, как известно, от знака первой производной функции. И из дифференциальных зависимостей (4.11), (4.12) следует:
· если на участке распределенная нагрузка q > 0 (действует вниз), то поперечная сила Q на этом участке является убывающей функцией;
· если на участке поперечная сила положительна, то функция М(x) возрастает;
· если на участке в каком-то сечении 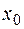 функция
функция 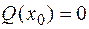 , то на эпюре М в этом сечении имеет место экстремум.
, то на эпюре М в этом сечении имеет место экстремум.
4. По знаку второй производной функции определяется выпуклость функции. Из зависимости (4.13) вытекает, что эпюра М всегда имеет выпуклость в сторону действия распределенной нагрузки (q – вниз, выпуклость – вниз и наоборот). По знаку второй производной от Q можно определить выпуклость эпюры Q. Из (4.11)
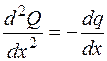
и, если q(x) – возрастающая функция, то 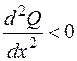 и эпюра Q имеет выпуклость вверх.
и эпюра Q имеет выпуклость вверх.
6. Из (4.11) следует, что
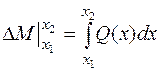 .
.
Это означает, что приращение изгибающего момента DМ на участке между сечениями х1 и х2 равно площади эпюры Q на указанном участке.
7. Из (4.12) получим:
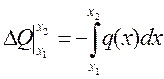 .
.
То есть приращение поперечной силы 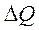 на участке между сечениями х1 и х2 равно площади графика
на участке между сечениями х1 и х2 равно площади графика 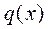 на этом участке. Например, если нагрузка q является равномерно распределенной, то площадь графика q равна
на этом участке. Например, если нагрузка q является равномерно распределенной, то площадь графика q равна 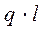 , где l – длина участка, на котором действует q.
, где l – длина участка, на котором действует q.
Примечание. Зависимости (4.11) и (4.12) и перечисленные правила справедливы, если начало отсчета x вести слева направо и эпюру М строить со стороны растянутых волокон.
Рекомендуем после построения эпюр обязательно проанализировать результаты, проверив выполняются ли все перечисленные правила в решенной Вами задаче.
Пример 1
Условие задачи
 Рис. 4.6. К решению примера 1 по построению эпюр Q и М:
а – схема балки с нагрузками;
б – эпюры поперечной силы и изгибающего момента
Рис. 4.6. К решению примера 1 по построению эпюр Q и М:
а – схема балки с нагрузками;
б – эпюры поперечной силы и изгибающего момента
|
Дана балка с действующими на нее нагрузками (рис. 4.6, а). Требуется определить внутренние усилия – поперечную силу Q и изгибающий момент М в балке, построить графики их изменения вдоль оси стержня (эпюры Q и М).
Решение
Прежде всего, найдем опорные реакции. Балка имеет жесткое защемление на правом конце[4] и в этом закреплении при заданной вертикальной нагрузке возникают две опорные реакции: вертикальная реакция RA и реактивный момент MA. Горизонтальная реакция при действии вертикальной нагрузки равна нулю. Это следует из уравнения равновесия "сумма проекций всех сил на горизонтальную ось равна нулю". Определим RA и MA, используя два других уравнения статики. Желательно составлять такие уравнения, в каждое из которых входит только одна неизвестная. В данном случае такими уравнениями являются "сумма проекций всех сил на вертикальную ось (ось z) равна нулю" и "сумма моментов всех сил относительно точки А равна нулю":
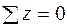 ;
;  ;
;
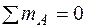 ;
; 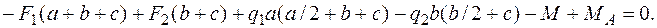 Из первого уравнения найдем RA = 30 кН, из второго – МА =5 кН×м. Полученные положительные знаки опорных реакций подтверждают выбранные нами направления опорных реакций: RA – вверх, а МА – против часовой стрелки. Для проверки рекомендуем использовать любое другое уравнение равновесия, например
Из первого уравнения найдем RA = 30 кН, из второго – МА =5 кН×м. Полученные положительные знаки опорных реакций подтверждают выбранные нами направления опорных реакций: RA – вверх, а МА – против часовой стрелки. Для проверки рекомендуем использовать любое другое уравнение равновесия, например 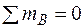 :
:
– 30×2 – 15×2×1 – 60 + 10×1×2,5 + 30×4+5 = – 150 + 150 = 0.
Теперь определяем внутренние усилия: поперечную силу Q и изгибающий момент М. В соответствии с методом сечений рассекаем балку на каждом участке (в данной задаче их три) произвольным сечением и рассматриваем все силы, расположенные с одной стороны от сечения: слева или справа. Удобно рассматривать все силы с той стороны от сечения, где сил меньше. Начало отсчета координаты x на каждом участке можно выбирать произвольным образом. Например, на рис. 4.6, а начало отсчета x на каждом участке – свое и находится в начале участка. Запишем выражения для Q и М на каждом участке.
Участок 1: 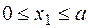 .
.
Рассмотрим силы, расположенные слева от сечения. По определению поперечной силы и с учетом правила знаков для Q (см. рис. 4.5, а):
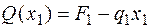 .
.
Здесь 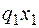 – равнодействующая равномерно распределенной нагрузки, действующей слева от сечения.
– равнодействующая равномерно распределенной нагрузки, действующей слева от сечения.
По определению изгибающего момента и с учетом правила знаков для М (см. рис. 4.5, б):
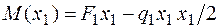 ,
,
где во втором слагаемом 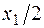 – плечо равнодействующей равномерно распределенной нагрузки (
– плечо равнодействующей равномерно распределенной нагрузки ( 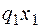 ), взятой слева от сечения (равнодействующая приложена по середине длины отсеченной части балки x1).
), взятой слева от сечения (равнодействующая приложена по середине длины отсеченной части балки x1).
Для построения эпюр найдем значения Q и М на границах участка:
в начале участка (х1 = 0) 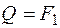 , а
, а  ;
;
в конце участка ( 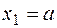 )
) 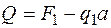 ;
; 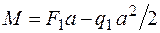 .
.
Участок 2: 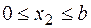 .
.
Снова рассмотрим все силы, расположенные слева от сечения.
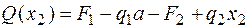 ;
;
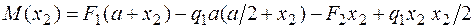 .
.
Граничные значения Q и М:
в начале участка ( 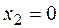 )
) 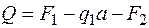 ;
;
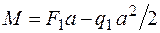 ,
,
в конце участка ( 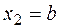 )
) 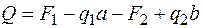 ;
;
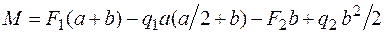 .
.
Участок 3: 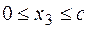 .
.
Теперь рациональнее рассмотреть все силы справа от сечения. Тогда
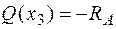 ;
;
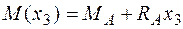 .
.
Из этих выражений следует, что поперечная сила на третьем участке – постоянная величина, а изгибающий момент меняется по линейному закону и на границах участка имеет следующие значения:
в начале участка ( 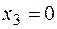 )
) 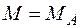 ,
,
в конце участка ( 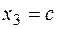 )
) 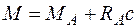 .
.
Запишем результаты определения внутренних усилий в таблицу, сосчитав численные значения Q и М на границах участков (табл. 1).
Таблица 1
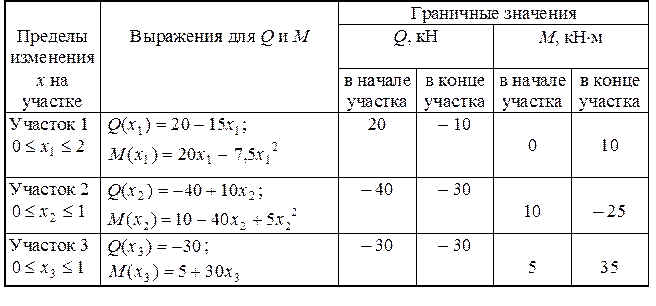
|
Из таблицы видно, что поперечная сила на первом участке меняет свой знак, т. е. график Q пересекает нулевую линию. Это значит, что изгибающий момент на этом участке имеет экстремум. Найдем максимальное значение М на этом участке. Сначала определим то значение координаты х1, при котором поперечная сила равна нулю. Обозначим это значение координаты х0 (см. рис. 4.6).
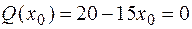 х0 = 1,33 м.
х0 = 1,33 м.
Чтобы найти максимальное значение изгибающего момента, подставим х0 в выражение для М на первом участке:
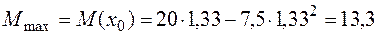 кН×м.
кН×м.
По результатам вычислений в таблице строим эпюры Q и М на каждом участке (см. рис. 4.6, б). Не забываем после построения эпюр проанализировать результаты по тем правилам проверки правильности построения эпюр, которые перечислены ранее.
Пример 2
Условие задачи
На балку кроме равномерно распределенной нагрузки действует линейно распределенная (треугольная) нагрузка (рис. 4.7, а). Построим эпюры распределения поперечной силы и изгибающего момента, обращая внимание на определение Q и М на участке с треугольной нагрузкой.
Решение
Найдем опорные реакции. Балка имеет шарнирное опирание и для определения двух не равных нулю опорных реакций RA и RB (горизонтальная реакция HA = 0) составим два независимых уравнения статики. Рациональными уравнениями, в каждое из которых входит одна неизвестная реакция, в данном случае являются:
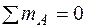 ;
; 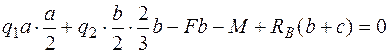 ,
,
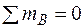 ;
; 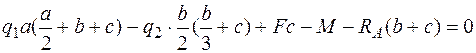 .
.
Напомним как определяется момент от треугольной нагрузки. Равнодействующая от треугольной нагрузки равна площади треугольника 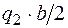 и приложена в центре тяжести треугольника, поэтому плечо этой равнодействующей относительно точки А равно
и приложена в центре тяжести треугольника, поэтому плечо этой равнодействующей относительно точки А равно  , а относительно точки В –
, а относительно точки В –  . Из этих уравнений найдем RA = – 31,9 кН, RB = – 18,1 кН. Отрицательные знаки показывают, что обе реакции направлены не вверх, как показано на рис. 4.7, а, а в противоположную сторону. Для проверки опорных реакций составим уравнение равновесия "сумма проекций сил на вертикальную ось z равна нулю":
. Из этих уравнений найдем RA = – 31,9 кН, RB = – 18,1 кН. Отрицательные знаки показывают, что обе реакции направлены не вверх, как показано на рис. 4.7, а, а в противоположную сторону. Для проверки опорных реакций составим уравнение равновесия "сумма проекций сил на вертикальную ось z равна нулю":
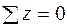 ;
; 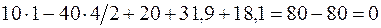 .
.
Определение внутренних усилий производим, записывая выражения для Q и М в таблицу (табл. 2).
Поясним выражения для Q и М на втором участке, а именно третьи слагаемые в этих выражениях, учитывающие треугольную нагрузку. Чтобы найти равнодействующую от треугольной нагрузки, расположенной слева от рассматриваемого сечения на участке длиной х2, определим интенсивность распределенной нагрузки в сечении х2, которая на рис. 4.7, а обозначена 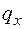 . Для этого составим пропорцию:
. Для этого составим пропорцию: 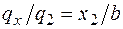 , откуда
, откуда 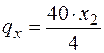 . Тогда равнодействующая этой распределенной нагрузки на участке длиной х2
. Тогда равнодействующая этой распределенной нагрузки на участке длиной х2 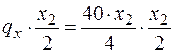 . Она приложена в центре тяжести треугольника, и изгибающий момент, создаваемый этой нагрузкой, равен
. Она приложена в центре тяжести треугольника, и изгибающий момент, создаваемый этой нагрузкой, равен 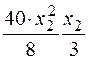 , где
, где 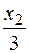 – плечо равнодействующей.
– плечо равнодействующей.
Таблица 2

|
Поскольку поперечная сила на втором участке меняет знак, найдем экстремальное значение изгибающего момента в сечении х0на этом участке (рис. 4.7, б). Определим величину х0, приравняв выражение для поперечной силы на втором участке нулю:
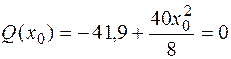 , откуда х0 = 2,89 м. Тогда
, откуда х0 = 2,89 м. Тогда
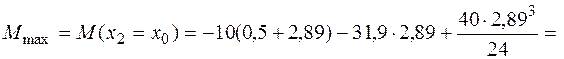
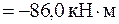
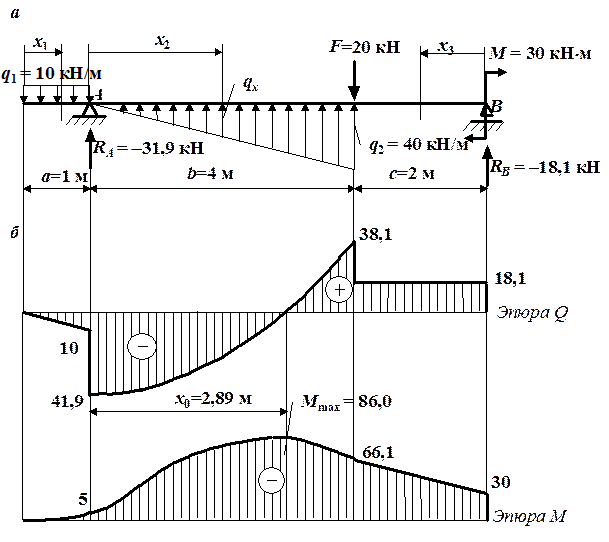 Рис. 4.7. К решению примера 2 по построению эпюр Q и М:
а – схема балки с нагрузками;
б – эпюры поперечной силы и изгибающего момента
Рис. 4.7. К решению примера 2 по построению эпюр Q и М:
а – схема балки с нагрузками;
б – эпюры поперечной силы и изгибающего момента
|
По полученным в таблице выражениям строим эпюры внутренних усилий. Напомним, что выпуклость эпюры М направлена в сторону распределенной нагрузки. Выпуклость эпюры Q на втором участке можно определить по знаку второй производной 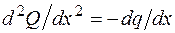 . В данном случае функция
. В данном случае функция 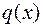 является убывающей, следовательно
является убывающей, следовательно 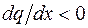 , а
, а 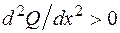 . Это означает, что эпюра Q имеет выпуклость вниз. Можно определить выпуклость эпюры поперечной силы и по-другому. В сечении, где интенсивность распределенной нагрузки равна нулю (начало второго участка в данной задаче), угол наклона касательной к кривой Q(x) должен равняться нулю, так как в этом сечении
. Это означает, что эпюра Q имеет выпуклость вниз. Можно определить выпуклость эпюры поперечной силы и по-другому. В сечении, где интенсивность распределенной нагрузки равна нулю (начало второго участка в данной задаче), угол наклона касательной к кривой Q(x) должен равняться нулю, так как в этом сечении 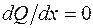 . Это возможно тогда, когда функция Q(x) имеет выпуклость вниз.
. Это возможно тогда, когда функция Q(x) имеет выпуклость вниз.
После того, как Вы нарисовали эпюры, рекомендуем обязательно проанализировать их по правилам проверки правильности построения эпюр.
4.1.2. Проверка прочности балок при плоском поперечном изгибе (задачи № 16–19)
Рекомендуемая литература:
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 6 (§ 6.1–6.3), гл. 7 (§ 7.1, 7.2), гл. 4 (§ 4.1, 4.2).
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 5 (§ 23–24), гл. 15.
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 7 (§ 7.6–7.8, 7.10), гл. 5 (§ 5.1–5.5).
Если Вы научились строить эпюры Q и М, то можете приступать к проверке прочности балок. Задача о проверке прочности балки чаще всего сводится к решению двух вопросов:
* подбору сечения балки, т. е. определению таких минимальных размеров поперечного сечения, которые удовлетворяют условиям прочности в опасных точках;
* определению грузоподъемности балки, т. е. нахождению такой максимальной нагрузки (допускаемой нагрузки) на балку, при которой удовлетворяются условия прочности во всех опасных точках.
Рассмотрим примеры проверки прочности балок круглого или прямоугольного сечений, двутавровых балок и балок произвольного моносимметричного сечения.
Пример 1
Условие задачи
На балку круглого поперечного сечения действует нагрузка, показанная на рис. 4.8, а. Требуется подобрать размеры поперечного сечения (или определить грузоподъемность балки) так, чтобы выполнялись условия прочности во всех опасных точках.
Решение
Строим эпюры Q и М (рис. 4.8, б). Эпюры Q и М нужны для того, чтобы найти положение опасных сечений и опасных точек в балке. Найдем положение опасных сечений для этой балки. Опасными сечениями в балках круглого и прямоугольного сечений являются:
* сечение, где действует максимальный по модулю изгибающий момент (сечение а–а на рис. 4.8, в);
* сечение, где действует наибольшая по абсолютной величине поперечная сила (сечение b–b на рис. 4.8, в).
В опасных сечениях находятся опасные точки –точки, в которых действуют либо максимальные нормальные, либо максимальные касательные напряжения. Чтобы найти положение опасных точек, посмотрим на эпюры распределения нормальных s и касательных t напряжений по высоте балки, которые построены на рис. 4.8, в. Из эпюры s видно, что наибольшие нормальные напряжения действуют в точках, наиболее удаленных от нейтральной оси y. Таким образом, опасными точками с максимальными нормальными напряжениями являются точки 1, 1¢, расположенные в сечении а–а (рис. 4.8, в). В одной точке действуют максимальные растягивающие напряжения, в другой – максимальные сжимающие. В данной задаче в сечении а–а максимальный момент положителен, т. е. он изгибает балку выпуклостью вниз, поэтому в точке 1 действуют растягивающие, а в точке 1¢ – сжимающие напряжения. Если допускаемые напряжения при растяжении и сжатии материала балки одинаковы (дерево или пластичный материал), то обе точки являются равноопасными. Опасная точка с максимальными касательными напряжениями, как видно из эпюры t, расположена на оси балки в сечении b–b, где действует наибольшая поперечная сила (точка 2 на рис. 4.8, в).
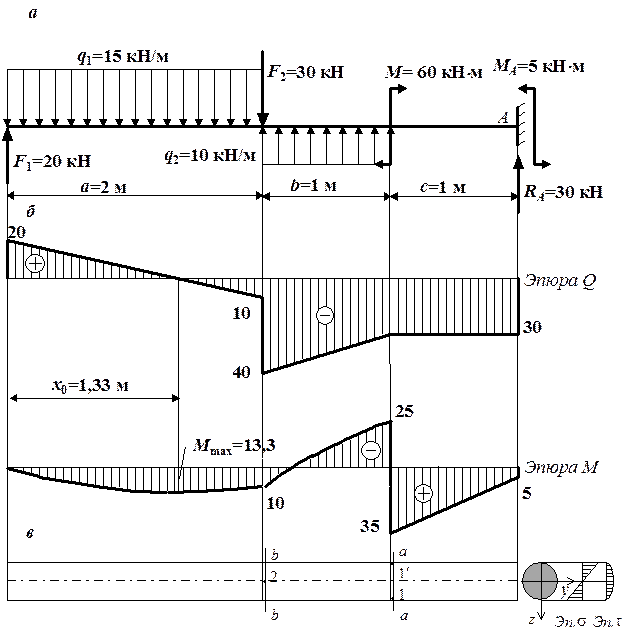 Рис. 4.8. К решению примера 1 о проверке прочности балки:
а – схема балки с нагрузками; б – эпюры внутренних усилий;
в – опасные сечения и опасные точки
Рис. 4.8. К решению примера 1 о проверке прочности балки:
а – схема балки с нагрузками; б – эпюры внутренних усилий;
в – опасные сечения и опасные точки
|
Запишем условия прочности в опасных точках. Начнем с рассмотрения опасных точек 1, 1¢, так как именно эти точки чаще всего бывают наиболее опасными. Эти точки находятся в линейном напряженном состоянии (рис. 4.9, а) и условие прочности в этих точках записывается так же, как при растяжении-сжатии:
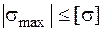 ,
,
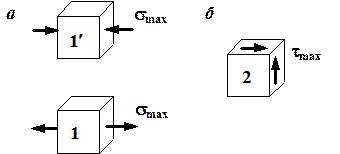 Рис. 4.9. Напряженное состояние опасных точек
Рис. 4.9. Напряженное состояние опасных точек
|
где максимальные напряжения определяем по формуле (4.3). Тогда условие прочности в точках 1, 1¢  будет иметь вид
будет иметь вид
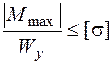 .
.
Если стоит задача подбора сечения, то из этого условия находим требуемый момент сопротивления балки:
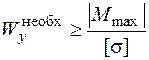 ,
,
а, зная момент сопротивления, по формулам (4.5) определяем размеры поперечного сечения балки. Например, для балки круглого поперечного сечения необходимый радиус 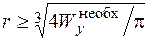 . Для деревянных балок диаметр ходовых бревен ограничен и не должен быть больше 26 см. Для бревна с радиусом 13 см момент сопротивления равен 1725 см3 . Если полученное из условия прочности значение необходимого момента сопротивления будет больше 1725 см3, то следует подобрать сечение из нескольких бревен. В рассматриваемом примере для деревянной балки с [s] = 10 МПа = 1кН/см2 найдем
. Для деревянных балок диаметр ходовых бревен ограничен и не должен быть больше 26 см. Для бревна с радиусом 13 см момент сопротивления равен 1725 см3 . Если полученное из условия прочности значение необходимого момента сопротивления будет больше 1725 см3, то следует подобрать сечение из нескольких бревен. В рассматриваемом примере для деревянной балки с [s] = 10 МПа = 1кН/см2 найдем 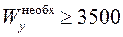 см3. Тогда количество бревен 3500/1725 = 2,1 » 3 (Округляем всегда в большую сторону). Момент сопротивления одного из трех бревен
см3. Тогда количество бревен 3500/1725 = 2,1 » 3 (Округляем всегда в большую сторону). Момент сопротивления одного из трех бревен 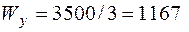 см3 и радиус каждого бревна будет
см3 и радиус каждого бревна будет 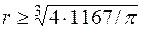 = 11,4 » 12 см. Заметим, что полученный результат (сечение из трех бревен с радиусом 12 см) справедливо, если все бревна располагать горизонтально, перпендикулярно плоскости изгиба.
= 11,4 » 12 см. Заметим, что полученный результат (сечение из трех бревен с радиусом 12 см) справедливо, если все бревна располагать горизонтально, перпендикулярно плоскости изгиба.
Если требуется определить грузоподъемность балки, то из условия прочности в точках 1, 1¢ находим максимальное значение изгибающего момента:
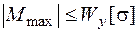 ,
,
которое зависит от нагрузки. Зная эту зависимость из эпюры М, найдем значение допускаемой нагрузки.
Решение задачи будет закончено только тогда, когда мы убедимся, что полученный размер поперечного сечения балки (или найденная допускаемая нагрузка) удовлетворяют условию прочности во второй опасной точке. Поскольку в точке 2 действуют только касательные напряжения (нормальные напряжения в точках, лежащих на оси балки, равны нулю – это видно из эпюры s на рис 4.8, в), то напряженное состояние этой точки – чистый сдвиг (рис. 4.9, б). Если неизвестно опытное значение допускаемого касательного напряжения, то условие прочности при чистом сдвиге записывается по соответствующей материалу балки теории прочности. Например, для пластичного материала из формул (4.9), (4.10) для чистого сдвига можно записать такие условия прочности для точки 2:
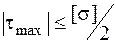 – по третьей теории и
– по третьей теории и
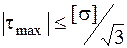 – по четвертой теории прочности.
– по четвертой теории прочности.
Для деревянной балки, а дерево – анизотропный материал, теории прочности, полученные для изотропных материалов, не справедливы. В этом случае для проверки прочности необходимо знать допускаемое значение касательного напряжения [t], полученное на основании опытных данных. Тогда для деревянной балки условие прочности в точке 2 записывается так:
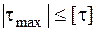 .
.
Здесь максимальное касательное напряжение 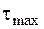 определяем в зависимости от формы поперечного сечения по формулам (4.6). Например, для рассматриваемой балки с подобранным сечением из трех бревен радиусом 12 см
определяем в зависимости от формы поперечного сечения по формулам (4.6). Например, для рассматриваемой балки с подобранным сечением из трех бревен радиусом 12 см
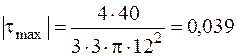 кН/см2,
кН/см2,
что меньше [t] = 2 МПа = 0,2 кН/см2.
Если условие прочности в точке 2 выполняться не будет, то необходимо подобрать сечение или найти грузоподъемность балки из условия прочности в этой точке.
Пример 2
Условие задачи
Стальная прокатная двутавровая балка загружена нагрузками, показанными на рис. 4.10, а. Подберем номер двутавра так, чтобы выполнялись условия прочности во всех опасных точках.
Решение
Строим эпюры Q и М. По построенным эпюрам Q и М (рис. 4.10, б) найдем положение опасных точек в двутавровой балке. Сначала покажем на фасаде балки опасные сечения. Кроме опасных сечений, где действуют максимальный изгибающий момент (сечение а–а на рис. 4.10, в) и наибольшая поперечная сила (сечение b–b на рис. 4.10, в), в двутавровой балке существует еще одно опасное сечение – это сечение, где Q и М одновременно имеют большие значения. В рассматриваемом примере это сечение с–с на рис. 4.10, в. В опасных сечениях находятся опасные точки. В сечении а–а – точки 1, 1¢ с максимальными нормальными напряжениями, в сечении b–b – точка 2, в которой действует наибольшее касательное напряжение. Особенностью проверки прочности двутавровой балки является появление новых по сравнению с балками круглого и прямоугольного сечений опасных точек. Это связано с особенностью эпюры распределения касательных напряжений по высоте двутавра. Точки 3, 3¢, находящиеся в сечении с–с и расположенные в крайних точках стенки на сопряжении с полкой (рис. 4.10, в), опасны, так как в них одновременно действуют большие нормальные и большие касательные напряжения.
Подберем размер двутавра (номер двутавра) из условия прочности в точках 1, 1¢ – именно эти точки являются, как правило, наиболее опасными, а затем проверим прочность в остальных опасных точках. Точки 1, 1¢ находятся в линейном напряженном состоянии (рис. 4.9, а) и условие прочности в этих точках имеет вид
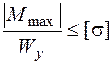 .
.
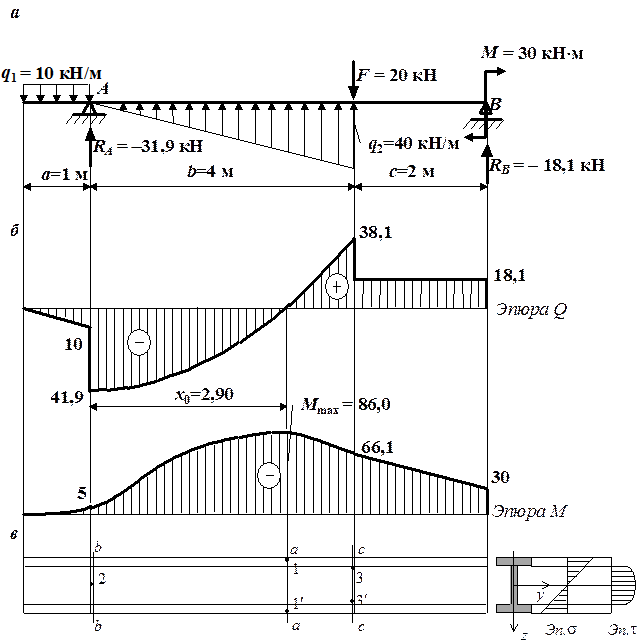 Рис. 4.10. К решению примера 2 о проверке прочности двутавровой балки:
а – схема балки с нагрузками; б – эпюры внутренних усилий;
в – опасные сечения и опасные точки
Рис. 4.10. К решению примера 2 о проверке прочности двутавровой балки:
а – схема балки с нагрузками; б – эпюры внутренних усилий;
в – опасные сечения и опасные точки
|
Отсюда определяем необходимый момент сопротивления 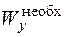 . По таблице сортамента прокатной стали (например, в [1]) подбираем номер двутавра, у которого момент сопротивления
. По таблице сортамента прокатной стали (например, в [1]) подбираем номер двутавра, у которого момент сопротивления 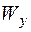 имеет близкое к
имеет близкое к 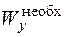 значение. (Обратите внимание, что в таблице сортамента – другое обозначение осей и принятому нами обозначению
значение. (Обратите внимание, что в таблице сортамента – другое обозначение осей и принятому нами обозначению 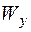 там соответствует
там соответствует 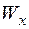 ). Для балки, изображенной на рис. 4.10, выполненной из стали с допускаемым напряжением 160 МПа,
). Для балки, изображенной на рис. 4.10, выполненной из стали с допускаемым напряжением 160 МПа,
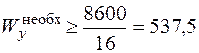 см3,
см3,
и в соответствии с ГОСТ 9239–89 подбираем двутавр № 33, у которого 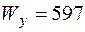 см3.
см3.
 Рис. 4.11. Отсеченные части сечения:
а – для точки 2;
б – для точки 3
Рис. 4.11. Отсеченные части сечения:
а – для точки 2;
б – для точки 3
|
После того, как найден номер двутавра, необходимо убедиться, что выполняются условия прочности в остальных опасных точках. Точка 2, в которой нормальные напряжения равны нулю, а касательные – максимальны, находится в напряженном состоянии "чистый сдвиг" и условие прочности в ней записывается по теории прочности, справедливой для пластичных материалов (4.9) или (4.10). Максимальные касательные напряжения находим по формуле Журавского (4.2). Рассмотрим подробно как находить статический момент отсеченной части 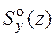 , входящий в формулу Журавского. Статический момент отсеченной части зависит от того, где находится точка, в которой определяется касательное напряжение. Чтобы найти отсеченную часть, надо мысленно разрезать поперечное сечение через точку, в которой ищем t, перпендикулярно направлению касательного напряжения. Любая из "отрезанных" частей может считаться отсеченной. Для точки 2 отсеченная часть сечения показана на рис. 4.11, а (заштрихованная часть) – это половина сечения. Для простых фигур (прямоугольник, круг), положение центра тяжести которых известно, статический момент находится по формуле
, входящий в формулу Журавского. Статический момент отсеченной части зависит от того, где находится точка, в которой определяется касательное напряжение. Чтобы найти отсеченную часть, надо мысленно разрезать поперечное сечение через точку, в которой ищем t, перпендикулярно направлению касательного напряжения. Любая из "отрезанных" частей может считаться отсеченной. Для точки 2 отсеченная часть сечения показана на рис. 4.11, а (заштрихованная часть) – это половина сечения. Для простых фигур (прямоугольник, круг), положение центра тяжести которых известно, статический момент находится по формуле
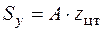 ,
,
где А – площадь фигуры; 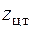 – координата центра тяжести (при вычислении статического момента отсеченной части знак координаты не учитывается, в этом случае
– координата центра тяжести (при вычислении статического момента отсеченной части знак координаты не учитывается, в этом случае 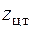 – это расстояние от центра тяжести отсеченной части до оси y). Для вычисления статического момента отсеченной части, показанной на рис. 4.11, а , разобьем ее на два прямоугольника: полку и половину стенки. Для каждого прямоугольника находим площадь и расстояние от центра тяжести до оси y. Тогда
– это расстояние от центра тяжести отсеченной части до оси y). Для вычисления статического момента отсеченной части, показанной на рис. 4.11, а , разобьем ее на два прямоугольника: полку и половину стенки. Для каждого прямоугольника находим площадь и расстояние от центра тяжести до оси y. Тогда
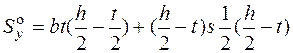 .
.
В этой формуле первое слагаемое – статический момент полки, а второе – статический момент половины стенки. Заметим, что для стандартных двутавров статический момент половины сечения задан в сортаменте (обозначен  ) и для найденного двутавра № 33
) и для найденного двутавра № 33 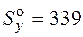 см3. В формуле Журавского (4.2) для точки 2
см3. В формуле Журавского (4.2) для точки 2 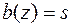 – толщина стенки двутавра,
– толщина стенки двутавра,  – осевой момент инерции находим по таблице сортамента прокатных двутавров (обозначен
– осевой момент инерции находим по таблице сортамента прокатных двутавров (обозначен  ) . Подставляя данные для двутавра № 33, получим
) . Подставляя данные для двутавра № 33, получим
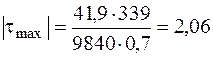 кН/см2.
кН/см2.
Сравнивая максимальное касательное напряжение согласно третьей теории прочности с 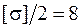 кН/см2 , убеждаемся, что условие прочности в точке 2 выполняется.
кН/см2 , убеждаемся, что условие прочности в точке 2 выполняется.
Проверим прочность в точках 3, 3¢, которые находятся в "балочном" напряженном состоянии (см. рис. 4.4). Найдем напряжения, действующие в точке 3. Нормальное напряжение ищем по формуле (4.1). Координата точки 3 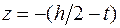 и
и
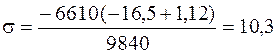 кН/см2.
кН/см2.
Положительный знак полученного напряжения показывает, что в точке 3, расположенной выше нейтральной оси, действует растягивающее напряжение. Для определения касательного напряжения по формуле Журавского получим сначала статический момент отсеченной части. Отсеченной частью сечения для точки 3 будет полка (см. рис. 4.11, б) и
 см3.
см3.
Так как точка 3 находится в стенке двутавра, то 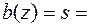 0,7 см. Тогда касательное напряжение в точке 3
0,7 см. Тогда касательное напряжение в точке 3
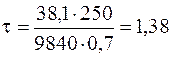 кН/см2.
кН/см2.
Подставляя найденные значения s и t в условие прочности по третьей теории (4.9), убеждаемся в том, что оно удовлетворяется:
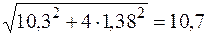 < 16 кН/см2.
< 16 кН/см2.
На этом процесс подбора двутавра заканчивается.
Примечание. В условии задачи № 17 есть пункты 7 и 8 [4].в которых требуется исследовать напряженное состояние произвольной точки двутавра. (Выполнение этой части задачи необязательны для студентов заочной формы обучения, студенты дневной и вечерней форм обучения могут выполнять эти пункты по требованию преподавателя) Эта часть задачи не имеет отношения к проверке прочности двутавра, носит академический характер и необходима для лучшего освоения теории изгиба. После того, как Вы выбрали произвольную точку, расположенную в сечении, где и Q, и М не равны нулю, найдите нормальное и касательное напряжения в этой точке по формулам (4.1), (4.2), используя те навыки, которые Вы приобрели при определении напряжений в опасных точках. Выделите вокруг исследуемой точки элементарный параллелепипед (элемент) и покажите на рисунке действующие на гранях элемента напряжения с учетом их знаков. Дальше определите главные напряжения и положение главных площадок, применяя знания, полученные при изучении разд. 2 "Исследование плоского напряженного состояния" в [5]. Поверните на рисунке элемент по главным направлениям и покажите на его гранях главные напряжения.
Пример 3
Условие задачи
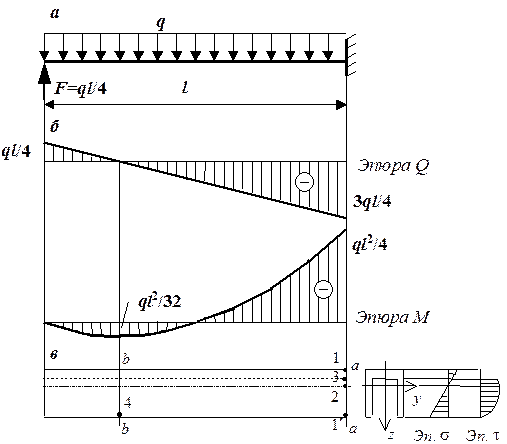 Рис. 4.12. К решению примера 3 о проверке прочности балки:
а – схема балки с нагрузками;
б – эпюры поперечной силы и изгибающего момента;
в – опасные сечения и опасные точки
Рис. 4.12. К решению примера 3 о проверке прочности балки:
а – схема балки с нагрузками;
б – эпюры поперечной силы и изгибающего момента;
в – опасные сечения и опасные точки
|
На балку моносимметричного сечения, выполненную из чугуна, действует нагрузка, показанная на рис. 4.12, а. Поперечное сечение балки изображает рис. 4.13. Надо найти грузоподъемность балки, т. е. значение допускаемой нагрузки, при которой обеспечена прочность балки.
Решение
Найдем геометрические характеристики заданного поперечного сечения: осевые моменты инерции относительно главных центральных осей. Сечение имеет только одну ось симметрии, эта ось является одной из главных осей инерции. Обозначим ее z. Вторая главная ось y проходит через центр тяжести сечения. Определим положение центра тяжести сечения по формуле
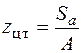 .
.
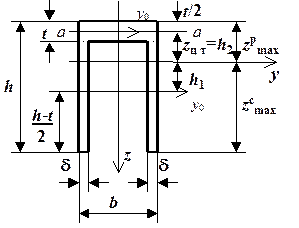 Рис. 4.13. Поперечное сечение
балки
Рис. 4.13. Поперечное сечение
балки
|
Статический момент 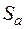 определяем относительно произвольной оси а–а, перпендикулярной оси z (оси симметрии), как сумму статических моментов фигур, составляющих заданное поперечное сечение. В данном случае сечение разбиваем на три прямоугольника и площадь сечения состоит из площадей трех фигур: двух стенок Ас и полки Ап:
определяем относительно произвольной оси а–а, перпендикулярной оси z (оси симметрии), как сумму статических моментов фигур, составляющих заданное поперечное сечение. В данном случае сечение разбиваем на три прямоугольника и площадь сечения состоит из площадей трех фигур: двух стенок Ас и полки Ап: 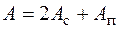 . Ось а–а рационально расположить так, чтобы статический момент одной из фигур равнялся нулю. Это произойдет, если ось а–а провести через центр тяжести какой-то фигуры, например, через центр тяжести полки (см. рис. 4.13). Тогда статический момент полки равен нулю и полный статический момент Sa равен удвоенному статическому моменту стенки:
. Ось а–а рационально расположить так, чтобы статический момент одной из фигур равнялся нулю. Это произойдет, если ось а–а провести через центр тяжести какой-то фигуры, например, через центр тяжести полки (см. рис. 4.13). Тогда статический момент полки равен нулю и полный статический момент Sa равен удвоенному статическому моменту стенки:
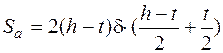 .
.
Здесь первый множитель – удвоенная площадь стенки, второй – координата центра тяжести стенки[5].
Найдя положение центра тяжести сечения, проведем через него вторую главную ось y (см. рис. 4.13). Рекомендуем рисовать сечение в масштабе, тогда по масштабу можно проконтролировать правильность определения центра тяжести сечения. В данном случае очевидно, что центр тяжести должен быть смещен к полке.
Теперь определим осевой момент инерции относительно оси y. Находим его как сумму моментов инерции трех фигур: двух стенок ( 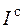 ) и полки (
) и полки ( 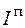 ). Для определения момента инерции каждой фигуры используем формулу
). Для определения момента инерции каждой фигуры используем формулу
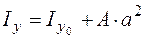 .
.
Здесь 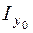 – момент инерции фигуры относительно оси y0, проходящей через центр тяжести фигуры и параллельной оси y, а – расстояние между осями y и y0. Таким образом,
– момент инерции фигуры относительно оси y0, проходящей через центр тяжести фигуры и параллельной оси y, а – расстояние между осями y и y0. Таким образом,
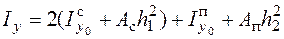 .
.
Расстояния h1 и h2 показаны на рис. 4.13. Моменты инерции полки и стенки относительно собственных осей y0 находим по формуле, справедливой для прямоугольника (4.4),
 ,
,
где b – ширина прямоугольника (параллельна оси y0); h – его высота. Например, для полки
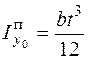 .
.
Примечание. Рекомендуем для тренировки аналогично найти момент инерции поперечного сечения относительно оси z, несмотря на то, что в проверке прочности этой балки он не участвует.
Строим эпюры поперечной силы и изгибающего момента, выражая ординаты через неизвестный параметр нагрузки (в данной задаче через q – см. рис. 4.12, б).
Прежде чем находить положение опасных сечений и опасных точек по эпюрам Q и М, выясним как рационально расположить поперечное сечение балки: полкой вверх или полкой вниз. Поскольку чугун – хрупкий материал и прочность при растяжении у него меньше прочности при сжатии, оптимальным положением сечения является такое положение, при котором максимальные растягивающие напряжения будут меньше максимальных по модулю сжимающих напряжений. В рассматриваемом примере максимальный изгибающий момент отрицателен, то есть балка в сечении, где действует 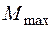 , изгибается выпуклостью вверх и растягивающие напряжения будут в верхних волокнах. Поэтому располагаем поперечное сечение так, чтобы центр тяжести сечения был ближе к верхним волокнам, т. е. полкой вверх.
, изгибается выпуклостью вверх и растягивающие напряжения будут в верхних волокнах. Поэтому располагаем поперечное сечение так, чтобы центр тяжести сечения был ближе к верхним волокнам, т. е. полкой вверх.
Найдем положение опасных сечений и опасных точек так же, как в двутавровой балке (см. рис. 4.12, в). Поскольку максимальная поперечная сила и наибольший изгибающий момент действуют в данном примере в одном сечении, то опасные точки 1, 1¢, 2 и 3 расположены в одном сечении а–а. Особенностью расчета балок из хрупкого материала является то обстоятельство, что точки 1 и 1¢ не являются равноопасными. Так как хрупкий материал имеет разную прочность при растяжении и сжатии, то проверять прочность надо как в точке 1, в которой действуют максимальные растягивающие напряжения, так и в точке 1¢ с наибольшими сжимающими напряжениями. Если эпюра изгибающих моментов меняет свой знак, как в рассматриваемом примере, то появляется еще одна опасная точка – точка 4 (см. рис. 4.12, в). В этой точке действуют растягивающие напряжения, и поскольку она расположена дальше от нейтральной оси, чем точка 1, величина растягивающего напряжения в точке 4 может оказаться больше, чем в точке 1 несмотря на то, что изгибающий момент в сечении b–b меньше, чем в сечении а–а.
Определим допускаемую нагрузку из условия прочности в точке 1, где действуют максимальные растягивающие напряжения:
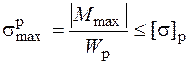 ,
,
откуда
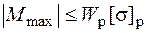 .
.
Здесь 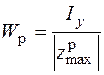 – момент сопротивления растяжению;
– момент сопротивления растяжению; 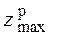 – расстояние до наиболее растянутого волокна показано на рис. 4.13. Для рассматриваемого примера
– расстояние до наиболее растянутого волокна показано на рис. 4.13. Для рассматриваемого примера 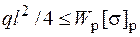 и
и 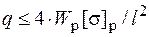 .
.
Проверим прочность в остальных опасных точках, используя найденное значение допускаемой нагрузки. В точке 1¢ с наибольшими сжимающими напряжениями
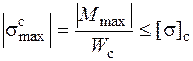 ,
,
где 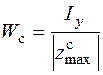 – момент сопротивления сжатию. (Расстояние
– момент сопротивления сжатию. (Расстояние 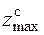 показано на рис. 4.13.)
показано на рис. 4.13.)
Для рассматриваемого примера опасной является и точка 4. Условие прочности в этой точке:
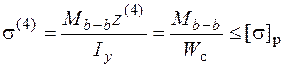 .
.
Чтобы проверить прочность в точке 2 с максимальными касательными напряжениями, находящейся в напряженном состоянии "чистый сдвиг", необходимо применить теорию прочности, справедливую для хрупкого материала. Например, из теории Мора (4.8) для чистого сдвига получим следующее условие прочности:
 ,
,
где максимальное касательное напряжение 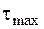 определяем по формуле Журавского (4.2), в которой статический момент
определяем по формуле Журавского (4.2), в которой статический момент 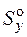 находим для отсеченной части, расположенной по одну (любую) сторону от нейтральной оси.
находим для отсеченной части, расположенной по одну (любую) сторону от нейтральной оси.
Наконец, условие прочности в точке 3, где действуют и нормальные (растягивающие), и касательные напряжения, записываем по теории прочности для "балочного" напряженного состояния, справедливой для хрупкого материала, например по теории Мора (4.8). Нормальные и касательные напряжения в этой точке определяем по формулам (4.1) и (4.2).
Если в какой-то точке условие прочности не будет выполняться, необходимо найти новое значение допускаемой нагрузки из условия прочности в этой точке.
Примечание; В рассматриваемой задаче, кроме условия прочности, должно выполняться и условие жесткости, т. е. максимальный прогиб не должен превосходить значения допускаемого прогиба. Эта часть задачи является необязательной. Вопрос о нахождении прогибов решается в следующем разделе "Определение перемещений и проверка жесткости балок".
4.1.3. Определение перемещений и проверка жесткости балок (задачи № 19, 20)
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 8 (§ 8.1–8.5, 8.9).
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 5 (§ 25), гл. 8.
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 7 (§ 7.13–7.14), гл. 11 (§ 11.4, 11.5).
Дата добавления: 2016-01-09; просмотров: 9630;
