Скорость волны в упругой среде. Стоячие волны.

Вычислим скорость распространения малых продольных возмущений в стержне, возни-кающих в результате действия постоянной силы , приложенной в некоторый момент времени к его свободному концу. Другой конец стержня закреплен (рис. 1).

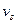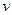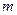Обозначим через - скорость распространения возмущения в стержне, а через - скорость движе-ния вещества в возмущенной области. При этом . Через обозначим массу деформированной части стержня в момент 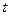. Тогда второй закон Ньютона для деформированной части примет вид:

.

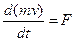За время 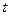возмущение проходит путь 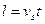. Тогда масса возмущенной части 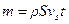. Выражая силу через нормальное напряжени 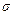, запишем второй закон в виде

.

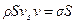Относительное удлинение возмущенной части стержня

.

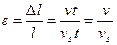Тогда с помощью закона Гука можно представить скорость движения возмущения в виде:

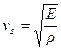. (1)

Для возбуждения продольной волны к концу стержня нужно приложить периодическую силу 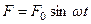. При этом скорость волны будет также определяться выражением (1).

Стоячие волны.

При наличии границ в упругой среде могут возникать колебания особого вида – стоячие волны. Они, например, возникают в натянутой струне с закрепленными концами. Для получения уравнения стоячей волны рассмотрим две одинаковые волны, распростра-няющиеся в противоположных направлениях:

, .

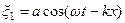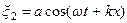По принципу суперпозиции для суммарного возмущения имеем

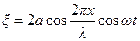. (2)

Уравнение (2) называется уравнением стоячей волны.

Из уравнения (2) следует, что амплитуда колебаний в стоячей волне зависит от .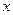

Максимумы амплитуды (пучности):

,

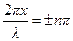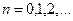
Минимумы амплитуды (узлы) :

.

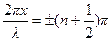Расстояние между узлами равно . Фаза колебаний частиц между узлами одинакова. Слева и справа от узла фаза отличается на 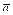(рис. 2).

Пример. Колебания струны, закрепленной на концах.

Для стоячей волны в струне длины 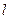должно выполняться условие

,

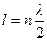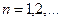
Следовательно, частоты возбуждаемых стоячих волн (собственные частоты колебаний струны) должны иметь значения

,

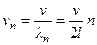где 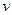- фазовая скорость волны в неограниченной струне. Очевидно, скорость волны должна зависеть от свойств струны. Найдем эту зависимость.

Скорость волны в натянутой неограниченной струне.

Перейдем к системе отсчета, движущейся со скоростью волны 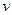. В такой системе форма изгиба струны будет неизменной, а она сама будет пролетать мимо наблюдателя со скоростью 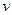. При этом мы пренебрежем скоростью поперечного движения частиц струны, считая колебания малыми. Выделим мысленно малый элемент струны длины и радиуса кривизны 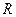вблизи “горба” волны (рис. 3). На его концы дейсвует сила натяжения 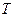. Тогда результирующая сила, действующая на него

.

Обозначим линейную плотность струны (массу единицы длины) через 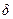. Тогда второй закон Ньютона для элемента можно записать в виде

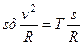. Отсюда находим .

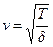ЛЕКЦИЯ 19