Отношение сходства и различия
Симметричные и рефлексивные нечеткие отношения сходства является аналогом отношения сходства или толерантности. Нечеткие отношения сходства обычно задаются в виде матрицы, при этом элементы этих матриц могут быть получены двумя способами:
1. Путем измерения некоторого физического параметра отражающего связь между объектами.
2. Путем опроса экспертов, эксперты для каждой пары объектов из универсума указывают их степень сходства в некоторой шкале, градациями которой могут быть значения терм – множества лингвистической переменной сходства.
Условия транзитивности для нечетких отношений сходства записывается в следующем виде:
S º S 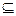 S , при этом в случае когда операция композиции отношений записывается в следующем виде:
S , при этом в случае когда операция композиции отношений записывается в следующем виде:
(R º S)(x, y)= 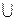 (R(x, z)
(R(x, z) 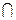 S(z, y))= sup {min (R(x, z), S(z, y))},
S(z, y))= sup {min (R(x, z), S(z, y))},
z 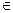 Z z
Z z 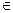 Z
Z
то это условие транзитивности может быть переписано следующим образом:
S(x, y)≥ S(x, z) 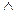 S(z, y),
S(z, y), 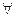 x, y, z
x, y, z 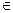 X
X
Данный вид транзитивности обозначается как ( 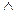 ) – транзитивность.
) – транзитивность.
Если L=[0, 1] и операцию 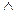 заменить на º (произведение), то условие транзитивности записывается в следующем виде:
заменить на º (произведение), то условие транзитивности записывается в следующем виде:
mS(x, y)≥ mS(x, z) º mS(z, y) и обозначается (º) – транзитивность.
Если L=[0, M], M< 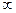 и операция
и операция 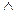
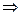
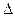 , то условие транзитивности записывается в следующем виде:
, то условие транзитивности записывается в следующем виде:
c 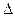 d=(c+d-M)
d=(c+d-M) 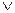 0,
0, 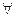 c, d
c, d 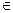 [0, M] и обозначается (
[0, M] и обозначается ( 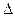 ) – транзитивность.
) – транзитивность.
В этом случае для нечетких отношений условие транзитивности можно записать таким образом:
S(x, y)≥S(x, z) 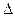 S(z, y),
S(z, y), 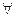 x, y, z
x, y, z 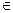 X
X
Наибольшее применение находит ( 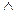 ) – транзитивность. Она является аналогом обычного отношения эквивалентности и называется нечетким отношением эквивалентности или подобия.
) – транзитивность. Она является аналогом обычного отношения эквивалентности и называется нечетким отношением эквивалентности или подобия.
Любой α – уровень нечеткого отношения эквивалентности является обычным отношением эквивалентности. Как известно обычное отношение эквивалентности разбивает все множество объектов на непересекающиеся классы эквивалентности.
Перейдем к рассмотрению симметричных и антирефлексивных нечетких отношений, называемых отношением различия D.
Мы зафиксировали, что отношение D является двойственным отношением сходства S.
В этом случае, когда L=[0, M], D(x, y)=M-S(x, y)
L=[0, 1], mD(x, y)=1 - mS(x, y)
В общем виде: D=┐S(Š)
Отношение различия удовлетворяют неравенству треугольника:
D(x, y)≥ D(x, z)+D(z, y), 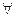 x, y, z
x, y, z 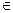 X
X
называется метрикой и обозначается как (+) – транзитивность.
Данное отношение различия является двойственным ( 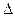 ) – транзитивному отношению сходства.
) – транзитивному отношению сходства.
Дата добавления: 2016-01-09; просмотров: 1017;
