Свойства нечетких отношений

Нечеткие отношения

Определение 12: нечетким бинарным отношением R на универсуме Ω называется нечеткое подмножество прямого произведения Ω 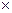Ω характеризующейся следующей принадлежности

μ_R : Ω 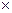Ω→[0,1]

Для конкретной пары элементов (ω_i, ω_j) 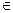Ω Ω 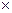степень принадлежности характеризует субъективную меру или степень выполнения нечеткого отношения ω_iR ω_j

Для случая когда универсум невелик и конечен, функция принадлежности нечеткого отношения может быть задана в виде матрицы:

М(R) = ║ М_R ║

Пример: Пусть универсум включает следующие элементы

Ω={1,3,5,7,9}

1 3 5 7 9

1 0 0 0 0 0

3 0,2 0 0 0 0

М(R) =5 0,4 0,1 0 0 0

7 0,8 0,5 0,1 0 0

9 1 0,8 0,5 0 0

Нечеткие отношения между элементами можно представить в графической форме в виде нечеткого ориентированного графа.

G(Ω, Ũ)

Ũ{<ω_i;ω_j> ;μ_R(ω_i;ω_j); μ_R(ω_i;ω_j)>0}

Пример:

ω₅ (9)

1 0,8 0,5

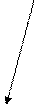
ω₁ (1) ω₄ (7)

0,8

0,2 0,4 0,5 0,1

ω₂ (3) 0,1 ω₃ (5)

Для нечетких отношений выполняются те же операции пересечения, объединения и дополнения как и для нечетких множеств. Записываются они так же.

Для нечетких отношений справедливо существование обратного отношения.

Если есть R то обратное отношение R^-1

ω_i R^-1 ω_j 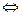ω_j R ω_i 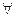ω_i, ω_j 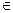Ω

μ _R-1(ω_i, ω_j) = μ_R(ω_i, ω_j)

Для нечетких отношений может быть задано произведение, при этом существует несколько способов представлений нечетких отношений.

Определение 1: Максиминное отношение

Пусть есть два нечетких отношения Ř₁, Ř₂ , тогда их произведение Ř₁˚Ř₂ могут быть определены следующим образом

μ _{Ř1˚ Ř2}(х,у) = sup max { μ _Ř1(x,z); μ _Ř2(z,y)}

z 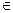Ω

Определение 2: Минимаксное

μ _{Ř1˚ Ř2}(х,у) = inf max { μ _Ř1(x,z); μ _Ř2(z,y)}

z 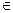Ω

Определение 3: Максмультипликативное

μ _{Ř1˚ Ř2}(х,у) = sup { μ _Ř1(x,z) 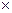μ _Ř2(z,y)} z 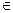Ω

Представление нечетких отношений с использованием α уровневых подмножеств (то есть класса Ф)

Множество α уровней нечеткого отношения R определяется следующим образом:

R_α={(x, y)½(x, y) 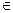X 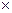X, m_R(x, y)≥α}

Матрицу множества уровня α можно получить из исходной матрицы отношения R, заменив в ней все элементы ≥α единицами, а остальные элементы нулем.

Разложение нечеткого отношения по четким множествам α уровня определяется точно также как разложение нечетких множеств.

Пример:

1 0,5 0 0,2

М_R= 0,3 1 1 0,4

0 0,6 0,5 0,1

1 0,7 0,3 0

1 1 0 0

0 1 1 0

M _Rα=0,5= 0 1 1 0

1 1 0 0

Свойства нечетких отношений

1. Рефлексивность

а) четкий случай

хRx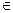, x X

в) нечеткий случай

R – рефлексивность, если 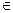x X

m _R(х, х)=1

2. Антирефлексивность

а) xRy, x≠y

в) m_R(x, x)=0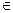, x X

(пример: R=<много больше>)

3. Симметричность

а) xRy 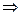yRx

в) m_R(x, y)= m_R(y, x)

(пример: R=<сильно различаются по величине>)

4. Антисимметричность

а) если (xRy)&(yRx), то х=у

в) m_R(x, y)>0 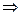m_R(y, x)=0

определение антисимметричного отношения, то есть в)

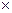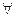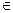m_R(x, y) m_R(y, х)=0 х, у Х

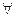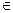min (m_R(x, y), m_R(y, х))=0 х, у Х

(пример: R=<много больше>)

5. Транзитивность

а) если (xRy)&(y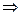Rz) (xRz)

в) R на множестве х транзитивно если R_º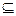R R ( 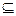- подмножество или включается)

поскольку это композиция – то оно зависит от способа определения данной композиции, отсюда можно выделить максиминную транзитивность, минимаксную и максмультипликативную транзитивность.

Обозначим через R₁⁽²⁾ – максиминное нечеткое отношение, R₂⁽²⁾ – минимаксное, R₃⁽²⁾ – максмультипликативное.

R⁽²⁾ – есть вторая проекция нечеткого отношения R, функция принадлежности которого

m _R(2) (у)= sup m_R(x, y)

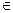x X

Для четкого случая:

R⁽²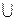⁾ = R(x) , где R(x)=(y\ xRy)

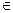x X

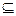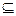Для нечетких отношений можно записать, что R₃⁽²⁾ R₁⁽²⁾ R₂⁽²⁾

Учитывая что

max (m_R(x, z), m_R(x, y))≥min (m_R(x, z), m_R(z, y))≥ m_R(x, z) ^. m_R(z, y), 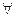x, y, z 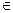X(Ω)

Из этих неравенств можно сделать вывод: что нечеткое отношение обладающее свойством минимаксной транзитивности обладает также транзитивностью двух других типов (максиминной и максмультипликативной), а нечеткое отношение обладающее максмультипликативной транзитивностью может не обладать транзитивностью двух других типов.