Собственные полупроводники. Понятие о дырках

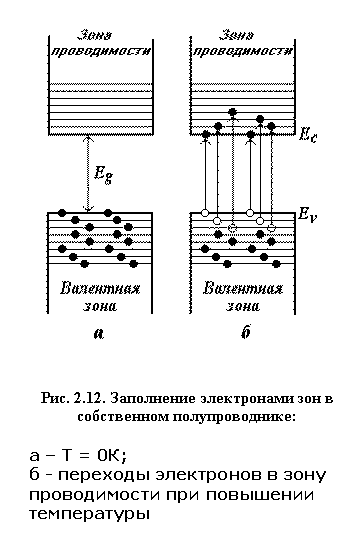
Из структуры энергетических зон полупроводников следует, что при абсолютном нуле они не проводят электрического тока. Нагревание их приводит к тому, что часть электронов валентной зоны приобретает энергию, достаточную для их перехода в зону проводимости, в результате чего появляется заметная электропроводность. С увеличением температуры число электронов в зоне проводимости увеличивается и вместе с этим растет электропроводность полупроводника. Тепловое возбуждение электронов проводимости иллюстрирует рис. 2.12. Е_с и Е_v обозначают дно зоны проводимости и потолок валентной зоны соответственно. Кроме температуры, возбуждение электронов проводимости может происходить и под действием других факторов, способных сообщить электронам энергию, достаточную для перехода их в зону проводимости. Этими факторами могут быть световое облучение, ионизирующее излучение и др.

Рассмотренный выше механизм возникновения электропроводности полупроводниковых кристаллов, справедлив для абсолютно чистых материалов, не содержащих примесей, влияющих на электропроводность. Такие полупроводники называются собственными, а их электропроводность собственной электропроводностью. К собственным полупроводникам относятся кристаллы чистых химических элементов, таких как германий (Ge), кремний (Si), селен (Se), теллур (Te) и др., а также некоторые химические соединения: арсенид галлия (GaAs), арсенид индия (InAs), антимонид индия (InSb), карбид кремния (SiC) и многие другие.

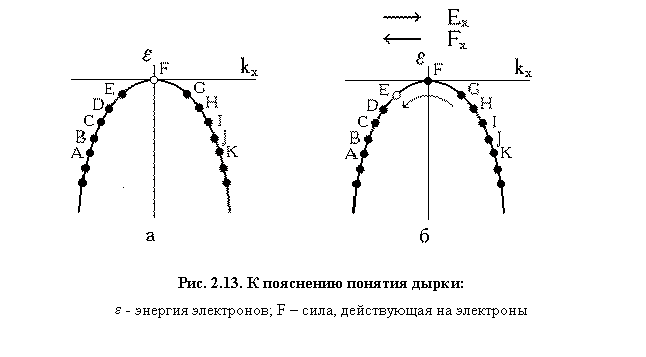
В разделе 2.8 показано, что электроны, расположенные у по-толка энергетической зоны, об-ладают отрицательной эффектив-ной массой. Именно такие электроны, расположенные у вершины валентной зоны, переходят в зону проводимости и участвуют в электропроводности полупроводника. Каждому электрону, перешедшему в зону проводимости, в валентной зоне соответствует незанятое (вакантное) состояние, которое называют дырочным состоянием. Дырочные состояния изображены на рис. 2.12 светлыми кружками. Наличие вакансий в валентной зоне позволяет электронам этой зоны изменять свое энергетическое состояние под действием внешнего электрического поля. Рассмотрим подробнее этот процесс на примере кристалла, в котором имеется одно вакантное состояние. В отсутствие электрического поля это состояние будет находиться в вершине зоны, т.к. электроны стремятся расположиться на уровнях с наименьшей энергией (рис. 2.13,а). Занятые электронами состояния изображены на рис. 2.13 точками и расположены на дисперсионной кривой, описывающей зависимость энергии электрона от компоненты волнового вектора k_x. У вершины энергетической зоны эта кривая приблизительно описывается параболой. Если к полупроводнику приложить внешнее электрическое поле Е (пусть для определенности оно будет направлено вдоль положительного направления оси х, рис. 2.13,б) , то у каждого электрона х-компонента волнового вектора k_x одновременно получит отрицательное приращение. Этот вывод следует из уравнения движения, одинакового для каждого электрона:

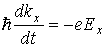. (2.20)

Следовательно, электроны валентной зоны будут перемещаться в направлении, указанном стрелкой на рис. 2.13,б. Вакантное состояние в результате этого движения электронов вначале переместится в точку Е, а затем - в точку D и т.д. Таким образом, последовательное перемещение электронов по энергетическим уровням под влиянием электрического поля эквивалентно перемещению вакантного состояния. Квантовое состояние, не занятое электроном в энергетической зоне, называется дыркой. Суммарный волновой вектор электронов в полностью заполненной энергетической зоне равен нулю, поскольку дисперсионная кривая симметрична относительно точки k = 0 и каждому электрону с волновым вектором k всегда найдется электрон с противоположным по знаку волновым вектором k. Если из состояния с волновым вектором k_e удален электрон, то полный волновой вектор системы станет равным k_e. Таким образом, дырке следует приписать волновой вектор

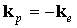. (2.21)

Учитывая (2.20) и (2.21), уравнение движения дырки будет иметь вид

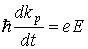. (2.22)

Это уравнение движения положительного заряда в электрическом поле. Поскольку дырка перемещается вдоль направления действующей на нее силы, то этой частице следует приписать положительную эффективную массу, равную по абсолютному значению отрицательной эффективной массе электрона, покинувшего вакантное состояние у потолка валентной зоны.

Вычислим ток, создаваемый электронами полностью заполненной энергетической зоны. Вклад в плотность тока от одного электрона, движущегося со скоростью v_j равен

.

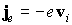Ток всех электронов валентной зоны равен сумме токов отдельных электронов:

.

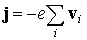Суммирование производится по всем состояниям, занятым электронами. Поскольку дисперсионные кривые симметричны, каждому электрону с ненулевым значением скорости в положительном направлении всегда найдется электрон с равной по абсолютному значению, но противоположно направленной скоростью. Следовательно, сила тока, создаваемого электронами полностью заполненной зоны, будет равна нулю.

Если в валентной зоне заняты все состояния, кроме одного, характеризующегося волновым вектором k_s и скоростью v_s (рис. 2.13,г), то суммарную плотность тока в этом случае можно представить в следующем виде:

.

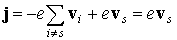В этой формуле учтено, что первое слагаемое в силу симметричности состояний электронов равно нулю.

Таким образом, движение электронов валентной зоны, в которой есть одно вакантное состояние, эквивалентно движению одной частицы с положительной эффективной массой и положительным электрическим зарядом, помещенной в это состояние.