Эффективная масса электрона в кристалле и ее физический смысл

Особенности движения электронов в кристалле обусловлены их взаимодействием с кристаллической решеткой. Оказывается, что движение отдельного электрона в кристалле можно описывать тем же уравнением, что и для свободной частицы, т.е. в виде второго закона Ньютона, в котором учитываются только внешние по отношению к кристаллу силы.

Рассмотрим движение электрона в кристалле под действием внешнего электрического поля. Внешнее электрическое поле приводит к увеличению скорости электрона и, следовательно, его энергии. Поскольку электрон в кристалле - это микрочастица, описываемая волновой функцией, то энергия электрона зависит от его волнового вектора. Зависимость между этими двумя характеристиками электрона в кристалле определяется дисперсионным соотношением, которое в свою очередь зависит от строения энергетических зон. Поэтому при расчете движения электрона в кристалле необходимо исходить из закона дисперсии.

Свободный электрон описывается монохроматической волной де Бройля и электрон в этом состоянии нигде не локализован. В кристалле же электрону необходимо сопоставить группу волн де Бройля с различными значениями частот 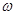и волновых векторов k. Центр такой группы волн перемещается в пространстве с групповой скоростью

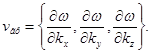
Эта групповая скорость соответствует скорости перемещения электрона в кристалле.

Задачу о движении электрона будем решать для одномерного случая. Увеличение энергии электрона dE под действием внешней силы F равно элементарной работе dA, которую совершает внешняя сила за бесконечно малый промежуток времени dt:

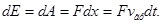(2.16)

Учитывая, что для электрона как микрочастицы 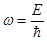, имеем следующее выражение для групповой скорости

Подставляя полученное выражение для групповой скорости в формулу (2.16), получим

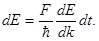
Отсюда

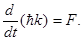
Распространяя этот результат на трехмерный случай, получим векторное равенство

(2.17)

Как видно из этого равенства, величина ћkдля электрона в кристалле изменяется со временем под действием внешней силы точно так же, как импульс частицы в классической механике 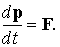Несмотря на это, ћkнельзя отождествить с импульсом электрона в кристалле, поскольку компоненты вектора k определены с точностью до постоянных слагаемых вида 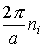(здесь a - параметр кристаллической решетки, n_i=1, 2, 3, ...). Однако в пределах первой зоны Бриллюэна ћkобладает всемисвойствами импульса. По этой причине величину ћk называют квазиимпульсом электрона в кристалле.

Вычислим теперь ускорение a, приобретаемое электроном под действием внешней силы F. Ограничимся, как и в предыдущем случае, одномерной задачей. Тогда

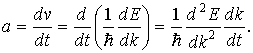
При вычислении ускорения учтено, что энергия электрона является функцией времени . Учитывая, что , получим

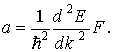(2.18)

Сравнивая выражение (2.18) со вторым законом Ньютона, видим, что электрон

в кристалле движется под действием внешней силы так, как двигался бы под действием той же силы свободный электрон, если бы он обладал массой

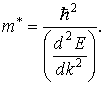(2.19)

Величину m* называют эффективной массой электрона в кристалле.

Строго говоря, эффективная масса электрона никакого отношения к массе свободного электрона не имеет. Она является характеристикой системы электронов в кристалле в целом. Вводя понятие эффективной массы, мы реальному электрону в кристалле, связанному взаимодействиями с кристаллической решеткой и другими электронами, сопоставили некую новую свободную “микрочастицу”, обладающую лишь двумя физическими параметрами реального электрона - его зарядом и спином. Все остальные параметры - квазиимпульс, эффективная масса, кинетическая энергия и т.д. - определяются свойствами кристаллической решетки. Такую частицу часто называют квазиэлектроном,электроном-квазичастицей,носителем отрицательного заряда или носителем заряда n-типа, чтобы подчеркнуть ее отличие от реального электрона.

Особенности эффективной массы электрона связаны с видом дисперсионного соотношения электрона в кристалле (рис.2.10). Для электронов, располагающихся у дна энергетической зоны, дисперсионное соотношение можно приблизительно описать параболическим законом

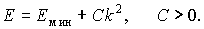
Вторая производная 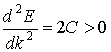, следовательно, эффективная масса положительная. Такие электроны ведут себя во внешнем электрическом поле подобно свободным электронам: они ускоряются под действием внешнего электрического поля. Отличие таких электронов от свободных состоит в том, что их эффективная масса может существенно отличаться от массы свободного электрона. Для многих металлов, в которых концентрация электронов в частично заполненной зоне мала и они располагаются вблизи ее дна, электроны проводимости ведут себя подобным образом. Если к тому же эти электроны слабо связаны с кристаллом, то их эффективная масса незначительно отличается от массы покоя реального электрона.

Для электронов, находящихся у вершины энергетической зоны (рис.2.10), дисперсионное соотношение можно приблизительно описать параболой вида

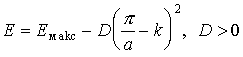
и эффективная масса является величиной отрицательной. Такое поведение эффективной массы электрона объясняется тем, что он при своем движении в кристалле обладает не только кинетической энергией поступательного движения Е_к, но и потенциальной энергией его взаимодействия с кристаллической решеткой U. Поэтому часть работы A внешней силы может перейти в кинетическую энергию и изменить ее на величину E_к, другая часть - в потенциальную U:

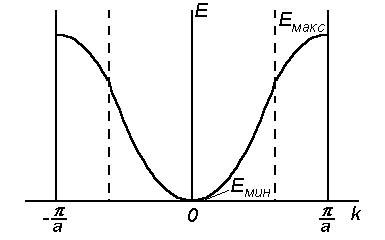
Рис. 2.10. Закон дисперсии для электрона в кристалле

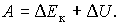
Рис. 2.11. Зависимость эффективной массы электрона от волнового числа

Если при движении электрона в потенциальную энергию переходит не только вся работа внешней силы, но и часть кинетической энергии, имевшейся у электрона (E_к < 0), то его скорость будет уменьшаться. В этом случае электрон ведет себя как частица с отрицательной эффективной массой. В случае, когда вся работа внешней силы переходит в потенциальную энергию (E_к = 0), то приращения кинетической энергии и скорости не происходит. Электрон ведет себя как частица с бесконечно большой эффективной массой.Бесконечно большой эффективной массой обладает электрон в точках перегиба дисперсионной кривой, которые на рис. 2.10 обозначены штриховыми линиями. Схематически зависимость эффективной массы электрона от его волнового числа показана на рис. 2.11.