Правило треугольника

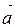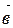Чтобы сложить векторы и , надо взять произвольную точку и от нее отложить последовательно сначала вектор 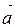, затем вектор 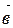. Вектор, начало которого совпадает с началом вектора 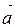(т.е. первого вектора), а конец – с концом вектора 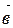(т.е. второго вектора), есть искомая сумма. На рис. 4 .

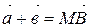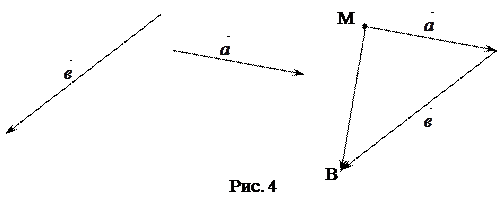
По правилу треугольника можно складывать любые векторы.

Коротко правило треугольника можно записать так:

для любых трех точек А,В и С .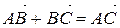

Правило параллелограмма

Чтобы сложить векторы 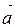и 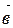, надо привести их к общему началу, т.е. взять произвольную точку А, построить такие точки В и С, что 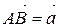и 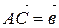, и достроить полученную фигуру до параллелограмма 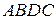. Вектор 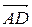- искомая сумма (рис. 5).

По правилу параллелограмма можно складывать тольконеколлинеарные векторы.

Свойства сложения векторов:

1⁰. .

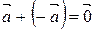
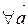2⁰. .

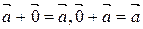
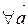3⁰. .

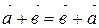
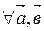4⁰. .

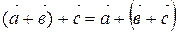
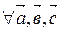Суммой трех векторов 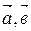и 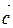называется вектор 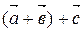. Учитывая свойство 4⁰, скобки можно опустить и обозначать сумму в виде .

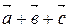Суммой n векторов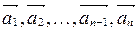называется вектор 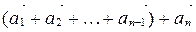и обозначается так: .

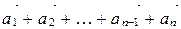При построении суммы n векторов пользуются правилом многоугольника.