Элементы векторной алгебры
Лекция 1
Векторы. Линейные операции над векторами
Понятие вектора
Направленным отрезком называется отрезок, у которого указаны начало и конец. Обозначение: 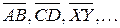
Вектором называется направленный отрезок. Обозначение: 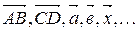 (рис. 1).
(рис. 1).
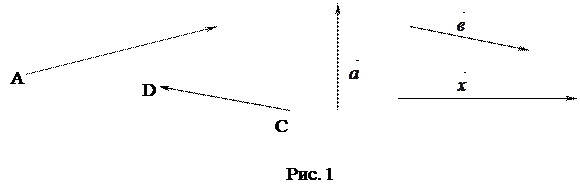 |
Вектор называется нулевым, если его начало и конец совпадают. Обозначение: 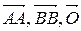 .
.
Векторы 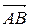 и
и 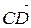 называются сонаправленными (противоположно направленными), если лучи [AB) и [CD) сонаправлены (противоположно направлены). Обозначение:
называются сонаправленными (противоположно направленными), если лучи [AB) и [CD) сонаправлены (противоположно направлены). Обозначение: 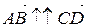 (
( 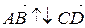 ).
).
На рис. 2 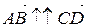 ,
, 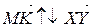 .
.
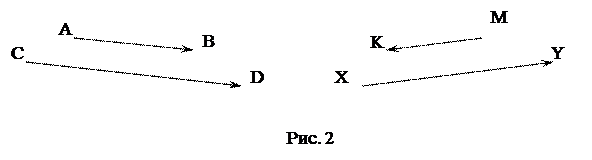 |
Векторы 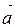 и
и 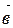 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначение:
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначение: 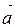 ||
|| 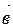 .
.
Нулевой вектор считается коллинеарным любому вектору.
Векторы 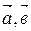 и
и 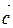 называются компланарными, если существует плоскость, которой они параллельны.
называются компланарными, если существует плоскость, которой они параллельны.
Длиной вектора называется расстояние между его началом и концом. Обозначение длины вектора 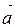 :
: 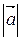 .
.
Длина нулевого вектора равна 0, т.е. 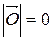 .
.
Вектор называется единичным, если его длина равна единице.
В пространстве существует бесконечное множество единичных векторов.
Два вектора называются равными, если они сонаправлены и длины их равны. Обозначение: 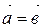 .
.
Два вектора называются противоположными, если они противоположно направлены и длины их равны.
Вектор, противоположный вектору 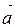 , обозначается
, обозначается 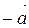 .
.
Откладыванием вектора 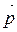 от точки А называется процесс построения такой точки М, что
от точки А называется процесс построения такой точки М, что 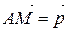 .
.
|

 Алгоритм этого процесса таков: пусть дан вектор
Алгоритм этого процесса таков: пусть дан вектор 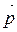 и точка А. Сначала строят луч
и точка А. Сначала строят луч 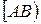 , исходящий из точки А и сонаправленный с вектором
, исходящий из точки А и сонаправленный с вектором 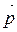 (рис. 3). Затем на луче
(рис. 3). Затем на луче 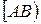 откладывают с помощью циркуля отрезок АМ, длина которого равна длине вектора
откладывают с помощью циркуля отрезок АМ, длина которого равна длине вектора 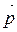 . Вектор
. Вектор 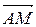 - искомый, т.е.
- искомый, т.е. 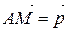 .
.
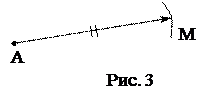 | |||
| |||
Дата добавления: 2015-11-28; просмотров: 667;
