Упражнения и задачи для самостоятельного решения
1. Дайте определение понятиям: «произведение растворимости», «растворимость»
2. Вычислите произведение растворимости хромата серебра, если в
500 мл воды при 25°С растворяются 0,011 г Аg2 СгО4.(1,2 ∙10–12)
Ответ: 1,2 ∙10–12
3. Произведение растворимости АgС1 равно 1,8∙10–10 . Вычислите растворимость соли (моль/л и г/л) в воде и 0,01М КС1. Коэффициенты активностей ионов принять равными 1.
Ответ:Растворимость в воде: 1,34 ∙10–5моль/л и 1,92 ∙10–3г/л ,
в растворе хлорида калия — 1,8∙10-8 моль/л и 2,58∙10-6г/л.
4. Смешали 10 мл 0,01М раствора СаС12и 40 мл 0.01М раствора оксалата аммония (NH4)2C2O4 . Выпадет ли осадок оксалата кальция, если ПРо(CaC2O4) =2∙10–9 ?
Ответ: да
5. В раствор, содержащий 0,01 моль/л BaCl2, и 0,01 моль/л SrCl2 , медленно добавляют раствор сульфата натрия. Какой осадок выпадет первым, если ПРо(BaSO4) =1,1 ∙10–10; ПРо(SrSO4)=3,2 ∙ 10–7?
Ответ: BaSO4
6. Во сколько раз уменьшится концентрация ионов серебра в насыщенном растворе хлорида серебра, если прибавить к нему столько соляной кислоты, чтобы её концентрация стала равной
0,03 моль/л?
ПРо(AgCl) = 1,8∙10-10.
Ответ: в 2200 раз
СТРОЕНИЕ АТОМА
Атом состоит из положительно заряженного ядра и электронов. Состояния электронов и других микрочастиц (протонов нейтронов и др.),их движения описываются квантовой механикой. Полная энергия внутреннего движения атомов и молекул принимает строго определённые квантовые значения. Законы движения приобретают вероятностный характер. Понятие траектории электрона внутри атомов и молекул теряет смысл. Одно из общих свойств материи является её двойственность — материя обладает одновременно и корпускулярными и волновыми свойствам. Корпускулярно-волновая природа частиц описывается уравнением де Бройля: λ=h/mV, где λ– длина волны,h–постоянная Планка( h=6,6310–34Дж∙с),m–масса частицы,
V–скорость частицы. Анализ этого уравнения показывает, что с уменьшением массы частицы и увеличением её скорости волновые свойства частицы усиливаются. Для описания корпускулярно-волновых свойств электрона в квантовой механике используется волновая функция Ψ. Квадрат её модуля /Ψ/2 представляет вероятность нахождения электрона в данной точке пространства. Основным уравнением квантовой механики является уравнение Шредингера:
∂2Ψ/∂x2 + ∂2Ψ/∂y2 + ∂2Ψ/∂z2 +8π2/mh2(Е – Еп)Ψ=0,
где Е – полная энергия электрона,Eп– потенциальная энергия электрона,m–масса электрона,Ψ –волновая функция. Решение уравнения Шредингера позволяет найти волновую функцию электрона Ψ(x,y,z) как функцию координат, которая называется орбиталью.Точное решение уравнения Шредингера известно для атома водорода и для одноэлектронных частиц. Для сложных атомов это уравнение может быть решено только приблизительно.
Для описания химических свойств элементов и соединений необходимо знать строение электронных оболочек атомов. Электрон – особая структура, имеющая отрицательный заряд, и обладающая свойствами как частицы, так и волны. Описание движения электрона в поле притяжении ядра атома с помощью классической механики невозможно. Для этого используются методы теории вероятности, общей теории электромагнетизма и квантовой механики.
Вероятность местонахождения электрона зависит от его энергетического состояния. Важно, что квадрат волновой функции |ψ|2 пропорционален вероятности нахождения электрона в определенной области пространства вблизи атома. Такая область получила название атомная орбиталь (АО). Графический образ – квадрат.


Орбиталь можно описать с помощью набора квантовых чисел: n –главное квантовое число,l –орбитальное квантовое число, ml –магнитное квантовое число.
Понятие АО вытекает из решения волнового уравнения и определяется как область пространства вблизи атомного ядра, вероятность нахождения электрона в которой максимальна и составляет 90-95%. Данная область имеет определенную форму, размеры и энергию, которые определяются набором 3-х т.н. квантовых чисел(n, l, ml), вытекающих из решения волнового уравнения.
n — главное квантовое число, которое может принимать значения любых целых чисел(1,2,3,4 …); оно определяет энергию электрона, а также размеры орбитали.
Совокупность атомных орбиталей с одинаковым значением n определяет энергетический уровень.
l — орбитальное квантовое число, которое при n=const последовательно принимает целочисленные значения от 0 до (n – 1); оно определяет пространственную форму орбитали.Орбитальному чилу l= 0 отвечают
s-орбитали, числу l=1– р-орбитали, числу l =2– d-орбитали. Совокупность атомных орбиталей с постоянным значением l при данном n образует энергетический подуровень .
ml — магнитное квантовое число, которое зависит от орбитального квантового числа; последовательно принимает целочисленные значения от (–l) до (+l), включая 0.Магнитное квантовое число mlопределяет ориентацию орбитали в пространстве.
Так, для p - энергетического подуровня (l=1) значения ml следующие:
–1, 0, +1. Таким образом, можно определить число атомных орбиталей на данном энергетическом подуровне, которое равно 2l + 1.
Подуровень, содержащий s-орбитали, называется s-подуровнем,
p-орбитали р-подуровнем, d- орбитали d-подуровнем, f-орбитали
f-подуровнем. Тогда, на s-подуровне имеется одна АО, на p-подуровне — три АО, на d-подуровне — пять АО, а на f -подуровне— семь АО.
Форма орбитали определяется орбитальным квантовым числом. Наиболее распространённый способ изображения орбиталей заключается в графическом предсталении граничной поверхности орбиталей.
Граничная поверхность ― часть электронной орбитали, в которой вероятность нахождения электрона имеет максимальное значение.
s-Орбитали симметричны для любого главного квантового числа n и отличаются друг от друга только размером сферы.
p-Орбитали существуют при n ≥ 2 и l = 1, поэтому возможны три варианта ориентации в пространстве: ml = –1, 0, +1. Все p-орбитали обладают узловой плоскостью, делящей орбиталь на две области, поэтому граничные поверхности имеют форму гантелей, ориентированных в пространстве под углом 90° друг относительно друга. Осями симметрии для них являются координатные оси, которые обозначаются px, py, pz.
d-Орбитали определяются квантовым числом l = 2 (n ≥ 3), при котором
ml = –2, –1, 0, +1, +2, то есть характеризуются пятью вариантами ориентации в пространстве. d-Орбитали, ориентированные лопастями по осям координат, обозначаются dz² и dx²–y², а ориентированные лопастями по биссектрисам координатных углов – dxy, dyz, dxz.
Семь f-орбиталей, соответствующих l = 3 (n ≥ 4), изображаются в виде граничных поверхностей, приведенных на рис.1.
Трёх квантовых чисел, выведенных при решении уравнения Шредингера, недостаточно для полного описания электронов в атоме, что следует из спектральных данных.Для интерпретации спектральных данных было введено спиновое квантовое число ms , которое имеет два значения – либо (+1/2), либо (–1/2) в зависимости от одной из двух возможных ориентаций спина электрона в магнитном поле. В квантовой механике устанавливается, что для электрона имеется дополнительная степень свободы, проявляющаяся в существовании особого момента количества движения (момента импульса), так называемого спина (от английского слова to spin–вращать веретено). Этот специфический момент количества движения, с которым связан соответствующий магнитный момент, существует независимо от орбитального движения.
Следовательно, состояние каждого электрона в атоме описывается набором 4-х квантовых чисел, три из которых относятся к атомной орбитали, которую он занимает и собственное спиновое квантовое число.
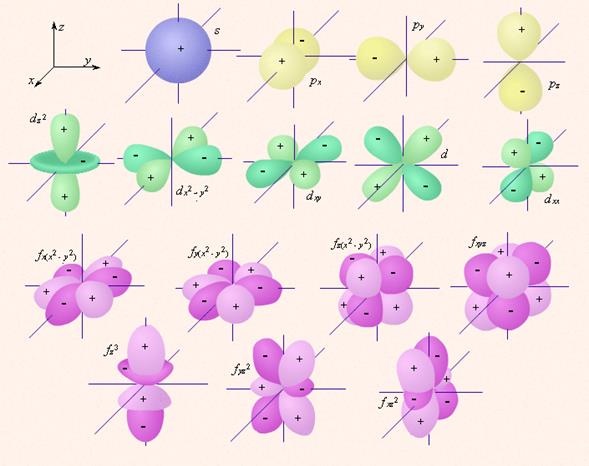
Рис. 1Изображение с помощью граничных поверхностей s-, p-, d- и
f-орбиталей.
Дата добавления: 2016-01-07; просмотров: 769;
