Цифровая обработка сигналов

Цифровая обработка сигналов (ЦОС; Digital Signal Processing, или DSP) – процесс выполнения по заданной программе вычислительных операций над числами, однозначно отображающими эти сигналы.

ЦОС получила широкое распространение благодаря бурному развитию микропроцессорной техники. ЦОС удобна и проста в использовании, обходится дешевле и выполняется надежнее, чем аналоговая обработка сигналов. Кроме того, DSP-системы дают возможность осуществлять такие операции, которые принципиально невозможны при аналоговой обработке (например, оцифрованную функцию можно сохранить в памяти компьютера, т.е. отложить обработку сигнала в реальном времени).

К достоинствам ЦОС относятся высокая гибкость и точность выполнения преобразований сигналов. Основным недостатком является ограниченное быстродействие.

Структурная схема СИСТЕМЫ ЦОС приведена на рисунке 25.1.

Рисунок 25.1 – Структурная схема системы ЦОС.

На вход системы ЦОС поступает аналоговый сигнал 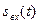. Входной фильтр низких частот (ФНЧ) отсекает паразитные частоты, которые лежат выше максимальной частоты информационного сигнала. В АЦП производится преобразование аналогового сигнала в цифровой с помощью операций дискретизации во времени, квантования по уровню и кодирования. Выходным сигналом АЦП является представляющая отсчеты входного сигнала последовательность двоичных чисел (x₀, x₁, x₂,…), составленных из нескольких разрядов. Каждому разряду соответствует своя шина, так что они возникают на выходе АЦП одновременно (параллельный код). Числа поступают в цифровой процессор (ЦП), который осуществляет над ними различные математические операции. Ранее полученные и промежуточные результаты могут сохраняться в памяти процессора для использования в последующих вычислениях. Результатом работы процессора является новая последовательность чисел (y₀, y₁, y₂,…), представляющих собой отсчеты выходного сигнала. Аналоговый выходной сигнал восстанавливается по этой последовательности чисел с помощью цифро-аналогового преобразователя (ЦАП). Сигнал на выходе ЦАП имеет ступенчатую форму. При необходимости он может быть преобразован в плавно меняющийся выходной сигнал s_вых(t) с помощью выходного ФНЧ, который отсекает все избыточные высокочастотные компоненты.

В цифровой форме можно создавать фильтры, анализаторы спектра, нелинейные преобразователи сигналов и др.

Цифровой фильтр

Фильтр – дискретная система, селектирующая или подавляющая те или иные диапазоны частот. Существуют четыре основных типа фильтров:

- фильтры низких частот (ФНЧ);

- фильтры высоких частот (ФВЧ);

- полосовые фильтры (ПФ);

- полосовые режекторные (заграждающие) фильтры (РФ).

Фильтры широко используются в системах связи для решения самых разных задач.

Например, селектирование одного из каналов в многоканальной системе, где отдельные каналы занимают смежные диапазоны частот; ограничение частот на входе приемника, благодаря чему любой шум и помехи на частотах, близких к полезному диапазону частот, эффективно отсекаются, позволяя улучшить качество работы системы в целом.

Фильтры могут быть

пассивными (электронные схемы, не содержащие активных элементов, т.е. транзисторов, операционных усилителей),

активными (электронные схемы, содержащие активные элементы; легко реализуется в виде интегральных микросхем),

цифровыми (специализированные ЭВМ или микропроцессоры).

Цифровой фильтр (ЦФ) - фильтр, реализованный на основе методов ЦОС, т.е. выполняющий преобразование входного цифрового сигнала в выходной цифровой сигнал на основе заданного алгоритма цифрового преобразования.

Рассмотрим линейные стационарные ЦФ.

Свойство линейности означает применимость принципа суперпозиции: если входные последовательности отсчетов порождают соответствующие им выходные последовательности отсчетов: 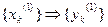, , 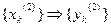- то при подаче входной последовательности, являющейся линейной комбинацией указанных воздействий, выходная последовательность будет представлять собой линейную комбинацию указанных откликов: .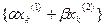

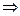
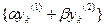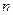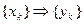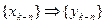Свойство стационарности означает, что задержка входной последовательности на тактов приведет к такой же задержке выходной последовательности: если , то . Например:

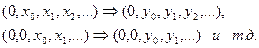
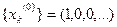
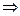
Чтобы проанализировать прохождение любого сигнала через линейный стационарный ЦФ, необходимо знать его импульсную характеристику, т.е. реакцию фильтра на единичный импульс: 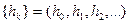. Существует два типа ЦФ:

- фильтры с конечной импульсной характеристикой (КИХ), имеющие конечную во времени импульсную характеристику;

- фильтры с бесконечной импульсной характеристикой (БИХ), имеющие бесконечную во времени импульсную характеристику.

Из свойств линейности и стационарности вытекает общий алгоритм линейной цифровой фильтрации:

,

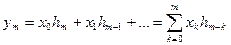где 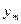- -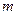ый отсчет выходного сигнала ;

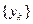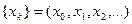- сигнал на входе ЦФ;

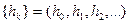- импульсная характеристика ЦФ.

Формула показывает, что выходная последовательность есть дискретная свертка входного сигнала и импульсной характеристики фильтра. Смысл формулы: в момент каждого отсчета ЦФ проводит операцию взвешенного суммирования всех предыдущих значений входного сигнала. Роль последовательности весовых коэффициентов играют отсчеты импульсной характеристики. Другими словами, ЦФ обладает некоторой памятью по отношению к прошлым входным воздействиям.