ГЛАВА 3. ФЕРМЫ. РАВНОВЕСИЕ ТЕЛ С УЧЁТОМ ТРЕНИЯ
В главе рассмотрены методы расчёта ферм, равновесие тел с учётом трения скольжения и трения качения и приведены примеры решения задач с учётом трения.
Фермы
Фермой называется неизменяемая конструкция, состоящая из стержней (рис. 51).
Основу фермы составляют геометрически неизменяемая фигура – треугольник.
| Рис. 51 |

Задача расчёта фермы включает определение опорных реакций и усилий в стержнях фермы.
При расчёте фермы вводятся следующие допущения:
1. Стержни в узлах фермы соединены идеальными шарнирами.
2. Весом стержней либо пренебрегают, либо разносят по узлам фермы.
3. Действующие на ферму силы приложены в узлах фермы.
При выполнении этих условий стержни фермы будут испытывать только сжимающие или растягивающие нагрузки. Причём если реакция стержня на узел направлена к узлу, то стержень сжат, если от узла – растянут (здесь аналогия с реакциями невесомого стержня на рис. 11).
Стержни, усилия в которых при заданных внешних силах равны нулю, называются нулевыми. Можно указать три признака наличия нулевых стержней в плоской ферме (леммы о нулевых стержнях).
1. Если в узле сходятся три стержня, на узел не действуют внешние силы и два стержня находятся на одной прямой, то третий стержень нулевой. По этой лемме усилия в стержнях 3 и 11 фермы на рис. 51 равно нулю.
2. Если в узле сходятся два стержня и узел не загружен внешними силами, то оба стержня нулевые (например, стержни 2 и 3 на рис. 52).
3. Если в узле сходятся два стержня и действующая на узел сила направлена по одному из них, то второй стержень нулевой (стержень 8 на рис. 52).
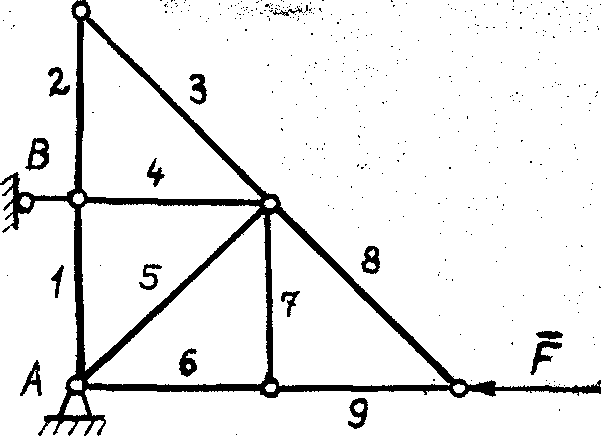
| Рис. 52 |
Для определения усилий в стержнях фермы обычно применяют метод вырезания узлов и метод Риттера. Рассмотрим эти два метода на примере фермы, изображенной на рис. 51.
Расчёт фермы любым методом начинается с определения опорных реакций.
1. Объект равновесия – ферма (рис. 53).
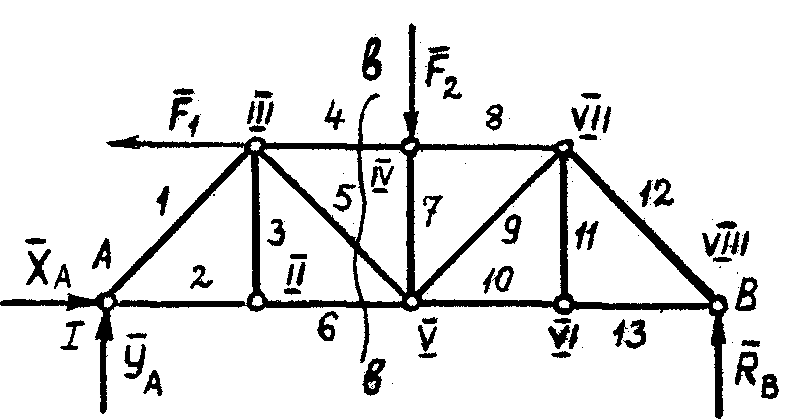
| Рис. 53 |
2. Внешние силы: 
Пусть 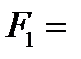 10 кН,
10 кН, 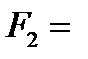 20 кН.
20 кН.
Реакции связей:  .
.
3. На ферму действует плоская произвольная система сил. Составляем три уравнения равновесия:
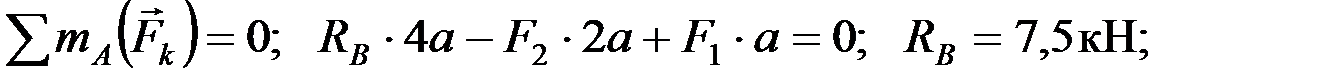

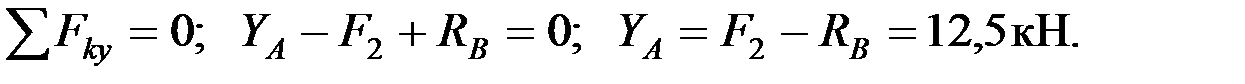
Метод вырезания узлов
Вырезаем узел, в котором сходятся два стержня (либо узел I, либо – VIII), например, узел I (рис. 54). Усилия 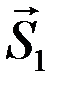 и
и  в разрезанных стержнях 1, 2 направляем вначале от узлов, т.е. считаем, что стержни растянуты. К узлу прикладываем действующие на него усилия
в разрезанных стержнях 1, 2 направляем вначале от узлов, т.е. считаем, что стержни растянуты. К узлу прикладываем действующие на него усилия 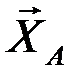 и
и 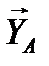 .
.
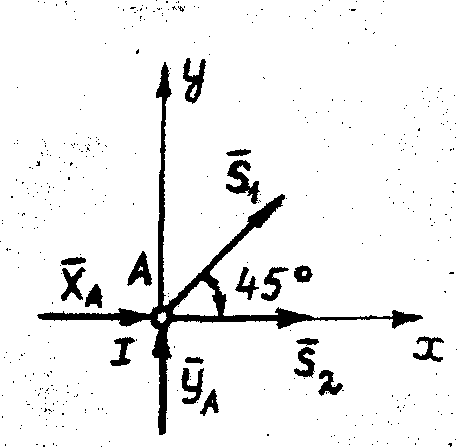
| Рис. 54 |
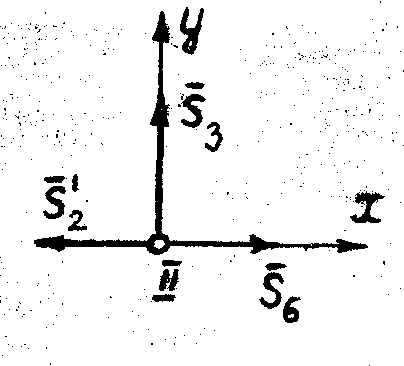
| Рис. 55 |
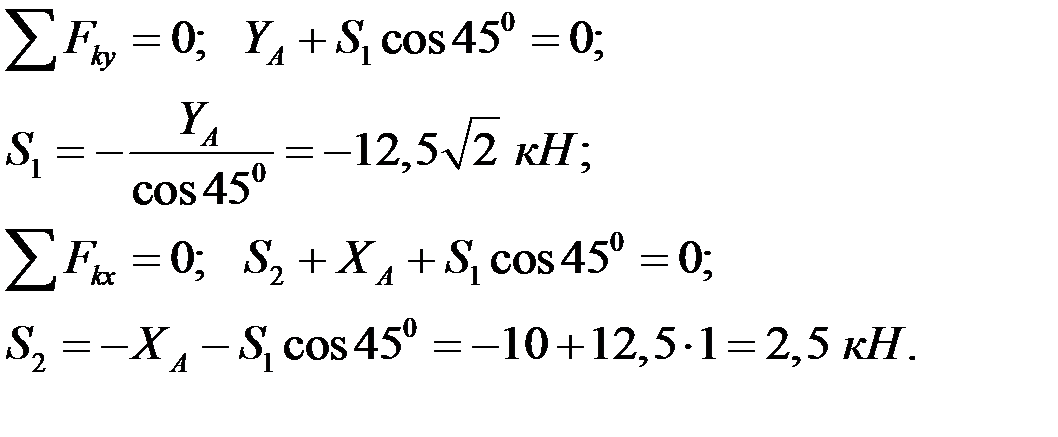
Так как усилие 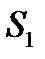 получилось со знаком «минус», то стержень I сжат.
получилось со знаком «минус», то стержень I сжат.
Далее выделяем узел, где имеется два новых стержня – узел II (рис. 55). К узлу II прикладываем усилия 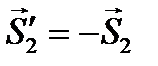 (согласно аксиоме действия-противодействия),
(согласно аксиоме действия-противодействия), 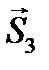 и
и 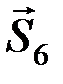 . Составляем два уравнения равновесия:
. Составляем два уравнения равновесия:
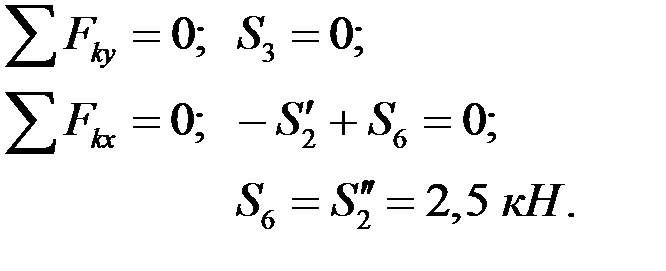
Далее последовательно вырезаем узлы III, IV, V, VI, VII, VIII. Следует oтмeтить, чтo при выделении пocлeднero узла VIII усилия в стержнях 12 и 13 будут уже определены при рассмотрении узлов VI, VII, поэтому два уравнения равновесия для этого узла можно считать проверочными. При правильном определении усилий в стержнях фермы уравнения равновесия для узла VIII должны дать тождество 0=0.
Метод Риттера
Этот метод позволяет определить усилие в любом стержне фермы без определения усилий в других стержнях. В этом преимущество этого метода перед методом вырезания узлов. Усилия в стержнях фермы по методу Риттера определяются после определения опорных реакций. Используя метод Риттера, определим, например, усилия в стержнях 4, 5, 6 фермы на рис. 53.
Для этого разрезаем ферму на две части сечением b-b (рис. 53) так, чтобы были разрезаны стержни, усилия в которых надо определить. Общее число разрезанных стержней не должно превышать трёх (в соответствии с тремя уравнениями равновесия для плоской произвольной системы сил). Для дальнейшего рассмотрения можно взять любую часть фермы, например левую (рис. 56). К выделенной части фермы прикладываем действующие на неё силы 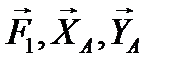 .
.
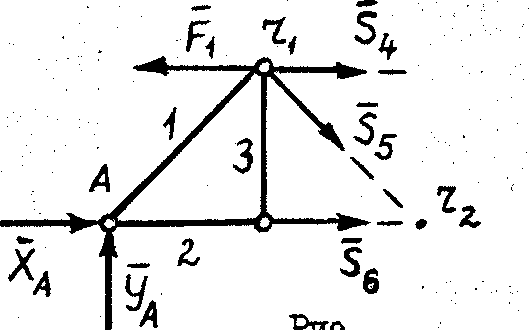
| Рис. 56 |
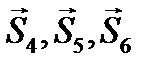 направляем вначале от узлов, т.е. считаем, что стержни растянуты. Составляем три уравнения равновесия для плоской произвольной системы сил, действующих на выделенную часть. Уравнения равновесия в методе Риттера составляем так, чтобы в каждое входило усилие только в одном разрезанном стержне. Это достигается путём выбора в качестве моментных точек Риттера – точек, где пересекаются усилия в двух разрезанных стержнях (точки
направляем вначале от узлов, т.е. считаем, что стержни растянуты. Составляем три уравнения равновесия для плоской произвольной системы сил, действующих на выделенную часть. Уравнения равновесия в методе Риттера составляем так, чтобы в каждое входило усилие только в одном разрезанном стержне. Это достигается путём выбора в качестве моментных точек Риттера – точек, где пересекаются усилия в двух разрезанных стержнях (точки 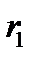 и
и 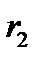 ), и соответствующего выбора осей, на которые проектируются силы
), и соответствующего выбора осей, на которые проектируются силы


| + |
| – |
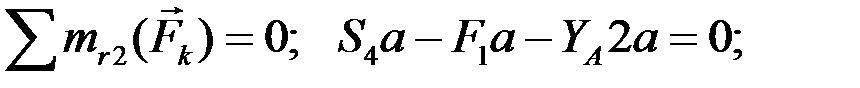
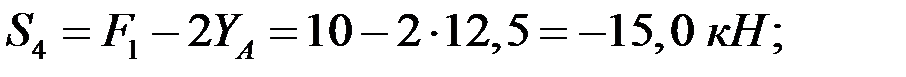
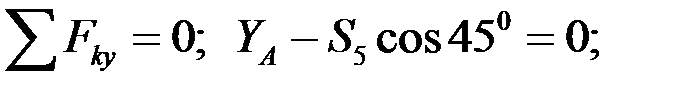

Трение скольжения
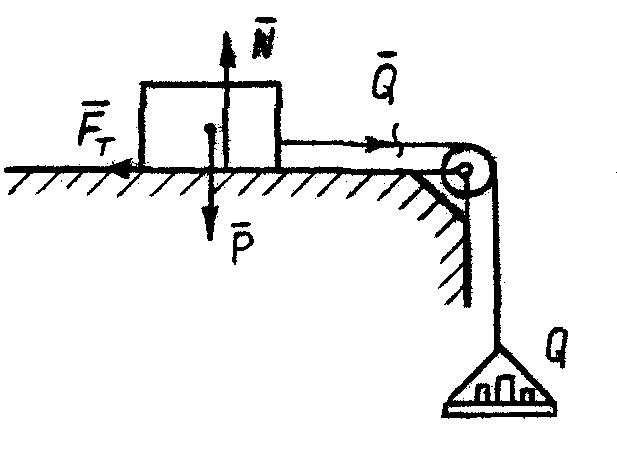
| Рис. 57 |
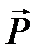 находится на шероховатой (реальной) поверхности. К телу с помощью нити, перекинутой через идеальный блок, подвешена чашка с разновесками, суммарный вес которых Q. Если Q мал, то тело А будет покоиться. Объясняется это тем, что на тело, кроме силы натяжения нити Q, веса
находится на шероховатой (реальной) поверхности. К телу с помощью нити, перекинутой через идеальный блок, подвешена чашка с разновесками, суммарный вес которых Q. Если Q мал, то тело А будет покоиться. Объясняется это тем, что на тело, кроме силы натяжения нити Q, веса 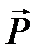 , нормальной реакции поверхности
, нормальной реакции поверхности  , в месте его контакта с поверхностью действует сила трения
, в месте его контакта с поверхностью действует сила трения  . Составим два уравнения равновесия для тела A:
. Составим два уравнения равновесия для тела A:
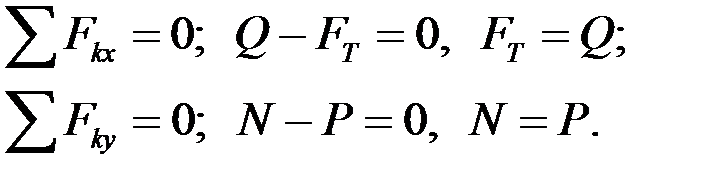
Очевидно, если Q = 0, то и сила трения  = 0, поэтому сила трения скольжения
= 0, поэтому сила трения скольжения  . Изучение равновесия тел при наличии трения скольжения базируется на законах Кулона - Амантона.
. Изучение равновесия тел при наличии трения скольжения базируется на законах Кулона - Амантона.
I. Сила трения направлена по общей касательной к соприкасающимся поверхностям в сторону, противоположную направлению возможного смещения тела.
II. Сила трения не зависит от площади поверхности контакта тел и не превышает некоторое предельное значение 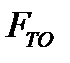 , поэтому
, поэтому
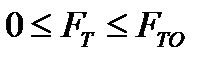 .
.
III. Предельное значение силы трения пропорционально нормальной реакции поверхности N:
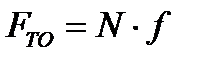 ,
,
где 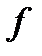 – безразмерный коэффициент пропорциональности, называемый коэффициентом трения скольжения.
– безразмерный коэффициент пропорциональности, называемый коэффициентом трения скольжения.
IV. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей (шероховатости, влажности, температуры, смазки и т.д.).
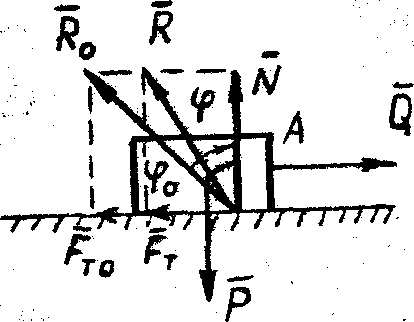
| Рис. 58 |
 и
и  являются реакциями поверхности, то
являются реакциями поверхности, то  есть полная реакция опорной поверхности, наклонённая к вертикали под углом
есть полная реакция опорной поверхности, наклонённая к вертикали под углом 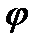 . Если сила трения приобретает свое предельное значение (что наблюдается при движении тела относительно опорной поверхности), т.е.
. Если сила трения приобретает свое предельное значение (что наблюдается при движении тела относительно опорной поверхности), т.е. 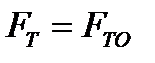 , то реакция поверхности
, то реакция поверхности 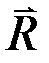 приобретает своё максимальное значение
приобретает своё максимальное значение 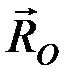 , равное
, равное  .
.
Угол 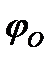 наклона максимальной реакции поверхности
наклона максимальной реакции поверхности 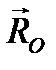 к вертикали называется углом трения. Из рис. 58 следует, что
к вертикали называется углом трения. Из рис. 58 следует, что
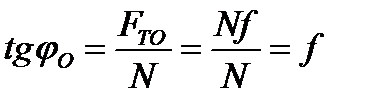 .
.
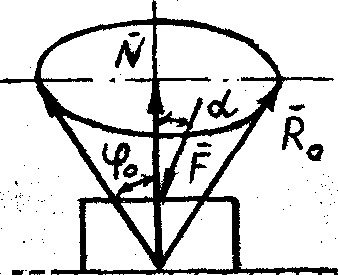
| Рис. 59 |
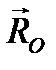 вокруг вертикали конус, то этот конус будет называться конусом трения (рис. 59). Рассмотрим случаи, когда на тело A действует сдвигающая сила
вокруг вертикали конус, то этот конус будет называться конусом трения (рис. 59). Рассмотрим случаи, когда на тело A действует сдвигающая сила 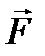 , приложенная внутри конуса трения (угол ее наклона к вертикали
, приложенная внутри конуса трения (угол ее наклона к вертикали 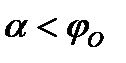 ).
).
Чтобы тело оставалось в покое, необходимо
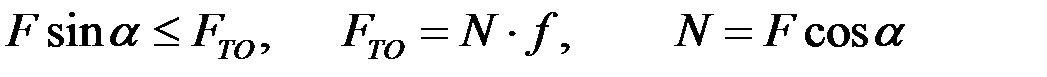 .
.
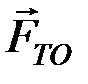
|
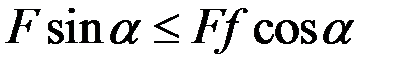 . Откуда
. Откуда 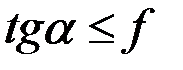 , но
, но 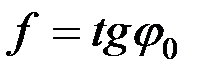 , поэтому
, поэтому  , т.е.
, т.е. 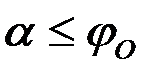 (условие покоя тела при действии силы
(условие покоя тела при действии силы 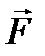 ). При выполнении условия
). При выполнении условия 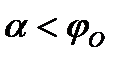 происходит самоторможение тела: сила, приложенная внутри конуса трения, не может сдвинуть тело с места при любой её величине.
происходит самоторможение тела: сила, приложенная внутри конуса трения, не может сдвинуть тело с места при любой её величине.
Задачи на равновесие тел с учётом трения скольжения решаются аналогично задачам, в которых на тела действует плоская произвольная система сил. Необходимо только ко всем действующим на тело силам прибавлять силу трения.
Пример
| Рис. 60 |
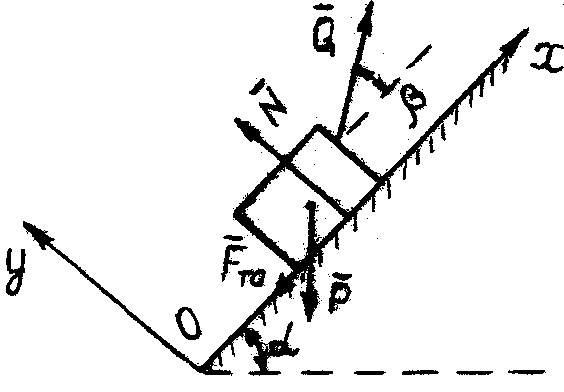
Тело весом Р (рис. 60) поднимается вверх по наклонной плоскости под действием силы  . Зная углы
. Зная углы  ,
, 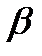 и угол трения
и угол трения  , определить, при каком угле наклона
, определить, при каком угле наклона 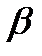 сила
сила  будет минимальной, и найти ее минимальную величину
будет минимальной, и найти ее минимальную величину 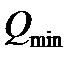 .
.
Решение
1. Объект равновесия – тело.
2. Активные силы: 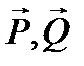 . Реакции связей:
. Реакции связей: 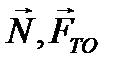 .
.
3. На тело действует плоская произвольная система сил:
| FТО |
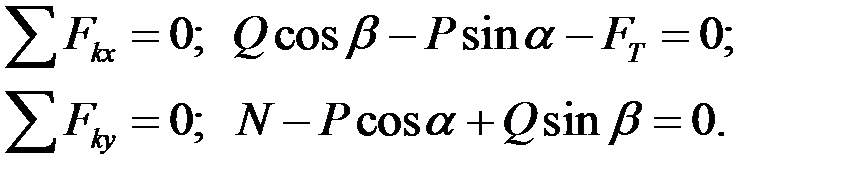 (3.1)
(3.1)
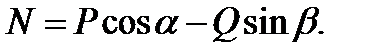
Сила трения
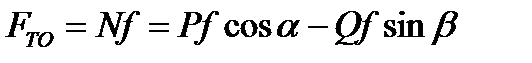 . (3.2)
. (3.2)
Подставляем уравнение (3.2) в выражение (3.1)
 (3.3)
(3.3)
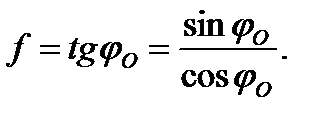 (3.4)
(3.4)
Подставляем уравнение (3.4) в формулу (3.3)

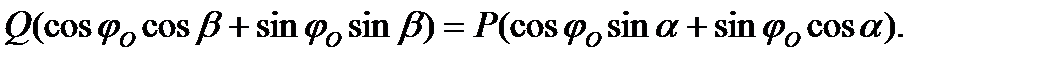
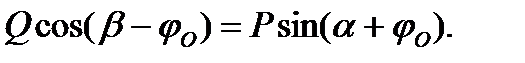 (3.5)
(3.5)
Очевидно, 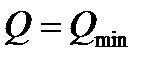 при
при 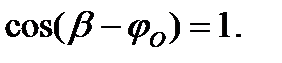 Значит ,
Значит , 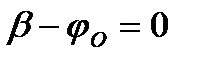 .
.
Следовательно, 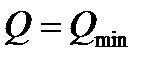 при
при 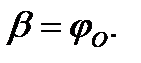
Из выражения (3.5)
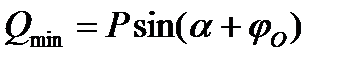 .
.
Трение качения
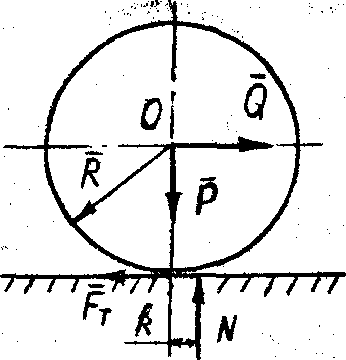
| Рис. 61 |
 (рис. 61). В точке контакта катка с поверхностью возникают сила трения скольжения
(рис. 61). В точке контакта катка с поверхностью возникают сила трения скольжения 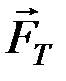 и нормальная реакция
и нормальная реакция  , которая в результате деформаций поверхностей контакта смещается на плечо k от линии действия силы тяжести P. Силы
, которая в результате деформаций поверхностей контакта смещается на плечо k от линии действия силы тяжести P. Силы  и
и  на плече k образуют пару сил (
на плече k образуют пару сил (  ,
,  ), момент которой называют моментом трения качения
), момент которой называют моментом трения качения
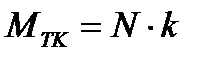 ,
,
где k – коэффициент трения качения, измеряется в единицах длины.
На рис. 61 силы 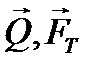 образуют пару, которая катит каток.
образуют пару, которая катит каток.
Чтобы каток катился, момент движущей пары должен быть больше (либо равен) пары момента трения качения:
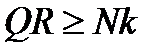 , откуда
, откуда 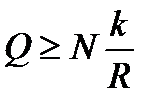 .
.
Чтобы каток катился без скольжения, сила Q не должна превышать предельного значения силы трения скольжения, значит, 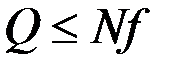 . Очевидно, справедливо неравенство
. Очевидно, справедливо неравенство
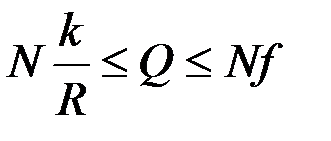 .
.
Следовательно, 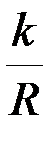 существенно меньше f.
существенно меньше f.
Полученное соотношение подтверждает, что каток легче катить, чем перемещать без качения. Так, переход в железнодорожном транспорте от подшипников скольжения на подшипники качения позволяет уменьшить движущую силу, которую должен развивать локомотив, чтобы двигать состав вагонов.
Пример
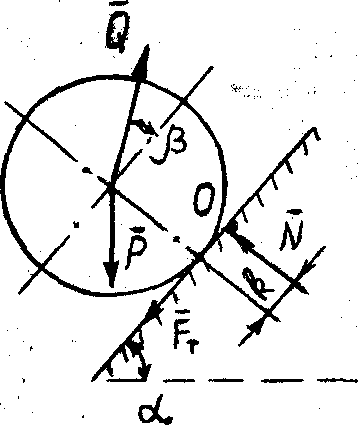
| Рис. 62 |
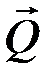 к плоскости –
к плоскости – 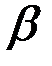 , коэффициент трения качения равен k.
, коэффициент трения качения равен k.
Решение
1. Объект равновесия – каток.
2. Активные силы: 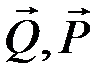 .
.
Реакции связей: сила трения скольжения 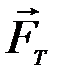 , нормальная реакция поверхности
, нормальная реакция поверхности 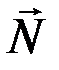 .
.
3. Для определения силы Q составим уравнение равновесия
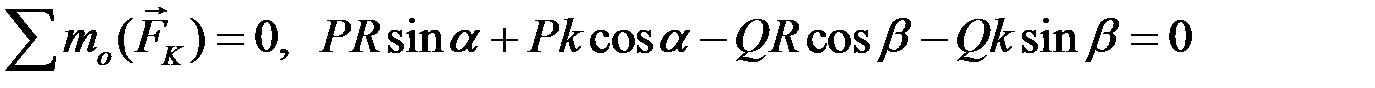 .
.
Отсюда  .
.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какая конструкция называется фермой?
2. Какие допущения вводятся при расчёте ферм?
3. В чём выражаются методы вырезания узлов и Риттера для определения усилий в стержнях фермы?
4. Что такое нулевые стержни и каковы признаки их наличия в ферме?
5. На каких законах базируется изучение трения скольжения и как читаются эти законы?
6. Что такое коэффициент трения скольжения?
7. Что называется конусом трения?
8. В чём выражается условие самоторможения тела?
9. Какова сущность трения качения? Что такое коэффициент трения качения?
10. Почему круглое тело легче катить, чем перемещать без качения?
Дата добавления: 2016-01-03; просмотров: 2587;
