Известно, что входы и выходы элементов систем управления – в теории

управления рассматриваются как носители информации, при этом следует

помнить, что исполнение принятого в управляющем устройстве решения

об оказании управляющего воздействия на объект связано с энергетически-

ми затратами, иногда значительными.

Для формирования управляющего воздействия можно использовать энер- гию самого управляемого процесса, отбираемой через измерительный эле- мент. В этом случае говорят о прямом регулировании.

Широко распространены поплавковые регуляторы уровня прямого дейст-вия, например, для карбюраторов автомобильных двигателей (см. рис.2.4). Здесь поплавок одновременно осуществляет три операции: измерение уров-

ня, принятие решения об указании управляющего воздействия и исполнение

решения. Аналогичный принцип регулирования уровня воды в котле паровой машины (принцип Ползунова), система автоматического регулирования час-

тоты вращения вала паровой машины с центробежным датчиком (принцип

Дж. Уатта). Следует отметить, что все приведенные примеры систем прямого

регулирования реализуют принцип управления по замкнутому циклу.

Достоинством систем прямого регулирования является простота и надеж-

ность, при этом не требуется посторонних источников энергии.

Недостатком этих систем является невысокая точность при необходимости

обеспечивать большие усилия для перемещения управляющих органов.

Для повышения точности управления объектами, требующих значительных

энергетических затрат на управление, необходимо разделение функций меж- ду измерительным и исполнительным элементами систем управления. В сис-

темах непрямого действия для оказания управляющего воздействия на объ-

ект необходим дополнительный источник энергии. На рис.2.5. представлена

принципиальная схема такой системы для стабилизации уровня жидкости,

т.е. система регулирования непрямого действия.

Достоинством систем непрямого управления является более высокая точ-

ность. Недостатком – большая сложность и стоимость, необходимость допол-

нительных источников энергии, меньшая надежность.

По виду используемой для управления энергии различают электрические,

механические, гидравлические, пневматические, электрогидравлические и

другие системы автоматического управления.

2.4. Задачи теории управления.

Основными задачами теории управления являются анализ и синтез систем

управления. Под анализом понимается выявление и количественная оценка

свойств поведения, а также объяснение свойств систем через характеристики

элементов и способ их взаимосвязи.

Важнейшими свойствами объектов и систем управления являются: устой-

чивость движений, инвариантность к возмущениям и робастность (грубость,

малая чувствительность). Синтез предполагает выбор элементов и связей ме-

жду ними таким образом, чтобы система имела требуемое поведение. Таким

образом, является задачей, обратной по отношению к анализу.

Важное значение для систем управления в технике имеют следующие пока-

затели: надежность, габариты, масса, энергопотребление, стоимость и эксп-

луатационные расходы, внешний вид и другие. Задача обеспечения соответ-

ствия этих показателей требованиям решается в процессе проектирования

систем управления. Эта задача выходит за рамки теории управления, в кото-

рой доминирует поведенческий аспект.

Реализация задач анализа и синтеза на реальных объектах возможно в ред-

ких случаях, так как это требует много времени, дорого, опасно и не всегда

осуществимо. Известно, что управляемый процесс может быть длительным

(печи и другие тепловые объекты), эксперименты – дорогими (запуск ракет)

и опасными (ядерные реакторы). При этом, объект управления часто проек-

тируется вместе с системой управления. Задачи синтеза и анализа в некото-

рых случаях можно решать с использованием физических моделей (анало-

гов) объектов.

Теория управления имеет дело с математическими (символьными) моделя-

ми. Построение математических моделей объектов и систем управления так-

же является задачей теории управления и смежных с ней дисциплин. Матема-

тические модели позволяют решать задачи анализа и синтеза аналитически

(расчетным путем) и путем имитации систем управления на компьютерах.

Математические модели систем управления.

Моделирование объектов и систем управления начинается с их выделения

из окружающей среды, что приводит к искажению изучаемых процессов, так

как в природе все явления в той или иной степени взаимосвязаны и взаимо- обусловлены. Динамические модели объектов и систем управления строятся

для объявления и предсказания их поведения – изменений во времени состо-

яния и наблюдаемых выходных переменных, вызванных внутренними про-

цессами и/или воздействиями среды.

Взаимодействие системы со средой.

Рассмотрение причинно-следственного взаимодействия системы управле- ния со средой связано с обособлением собственно системы S и выделением

ее связей со средой через переменные входа f и выхода у (рис.2.10).

f у

Среда

Рис.2.10.Взаимодействие системы со средой

Система оказывается звеном в искусственно разорванной цепи причинно-

следственных отношений “среда – система – среда”.

Операторы преобразования переменных.

На содержательном уровне объекты и системы управления интерпретирую-

тся как устройства получения, передачи и обработки информации. С другой

стороны, объекты и системы можно рассматривать как преобразователи сиг- налов – носителей этой информации. Преобразование сводится к изменению

параметров, кодирующих информацию.

Свойства системы как преобразователя характеризуется ее операторов, ото-

бражающим множество функций выхода:

у(t) = Q{f(t)} (2 – 6)

Примерами операторов являются оператор дифференцирования или диффе-

ренциальные уравнения

Ф(у, у’, у”,….,уⁿ; u, u’, u”,….,u^(m)) = 0, (2 – 7)

а также разностные уравнения:

Ф*(у(k),Dу(k),D²у(k),….,Dⁿу(k); u(k),D(k),…,D^mu(k)) = 0, (2 – 8)

где Dу(k) = у(k)-у(k-1); D²у(k) = Dу(k)-Dу(k-1) и т.д. – разности первого и вы-

сших порядков.

Оператор линеен, если обладает свойствами однородности и аддитивности.

Для линейного оператора справедливо:

- при любом усилении (ослаблении) входного воздействия выходная переме-

нная претерпевает точно такое же усиление, не изменяя своей формы;

- реакция на сумму любых входных воздействий равна сумме реакций на эти

воздействия.

В общем случае линейной комбинации входных воздействий отвечает та же

линейная комбинация соответствующих реакций:

Q{Sα_if_i(t)} = Sα_iQ{f_i(t)} (2 – 9)

^{i i}

Свойство линейности оператора, выраженное приведенной формулой, иног-

да называют принципом суперпозиции. Принцип суперпозиции дает возмож-

ность выражать реакцию линейной системы на любое воздействие через ее реакцию на определенный вид элементарных воздействий. Для этого произ-

вольное воздействие f(t) представляется как линейная комбинация элемента-

рных воздействий выбранного типа. Зная реакцию линейной системы на эле-

ментарные воздействия этого типа, определяется ее реакция на воздейст-

вие f(t).

Таким образом, линейная система как преобразователь полностью характе-

ризуется ее реакцией на типовое воздействие, называемой временной харак-

теристикой. Однако, в простейших случаях такая форма представления опе-

ратора наглядна, ее недостатком является неудобство решения задач анализа

и синтеза.

Если не выполняется принцип суперпозиции, то оператор называют нели-

нейным. При этом, класс нелинейных операторов много богаче линейных.

Оператор стационарен, если его характеристики инвариантны ко времени.

Другими словами, при сдвиге во времени входного воздействия без измене-

ния его формы реакция претерпевает такой же сдвиг во времени без приме-

нения своей формы. В ряде случаев модели должны отражать изменения

свойств объекта во времени; тогда вводятся в рассмотрение нестационарные

операторы у(t) = Q{f(t),t}. (2 – 10)

В простейшем случае нестационарность сводится к изменению параметров

модели, например коэффициентов дифференциального уравнения.

В общем случае влияние среды приводит к необходимости изменения стру-

ктуры оператора, например, порядка дифференциального уравнения или да-

же класса оператора.

Если вариации оператора происходят много медленнее основных процессов,

то вместо нестационарного оператора рассматривают множество стационар-

ных операторов, различающихся значениями параметров. Описание объекта

множеством равновероятных операторов содержит неопределенность. Всеоператоры модели заданы с точностью до интервалов значений, то такие сис- темы называются интервальные.

Оператор может быть детерминированным или стохастическим. В случае

стохастических операторов параметры представляются как случайные вели-

чины и задаются их вероятностными характеристиками. Объекты управления

могут быть с сосредоточенными или распределенными параметрами. В пос-

леднем случае они описываются уравнениями в частных производных.

Классы моделей.

Модель объекта или системы управления принадлежит тому же классу, что

и описывающий их оператор преобразования. Можно определить класс толь-

ко математической модели, а не реальный системы.

Таким образом, выделяют следующие признаки классов систем с непрерыв-

ным и дискретным временем:

- линейные (Л) или нелинейные (Л);

- стационарные (С) или нестационарные (С);

- детерминированные (Д) или стохастические (Д);

- сосредоточенные (конечномерные) (К) или распределенные (бесконеч-

номерные) (К).

Эти четыре независимые признака биальтернативны; поэтому можно нас-

читать всего 2⁴ = 16 классов непрерывных и столько же – дискретных систем.

Простейший класс ЛСДК – линейные стационарные детерминированные

конечномерные системы. Они имеют форму обыкновенных линейных диф-

ференциальных (разностных) уравнений с постоянными детерминированны-

ми коэффициентами. В математике разработан развитый аппарат анализа это-

го класса систем. При построении моделей стремятся к их максимальной простоте при достаточной адекватности оригиналам. Поэтому в первом приб-

лижении часто ограничиваются описанием объектов управления в классе ЛСДК.

Более сложные классы операторов получаются при введении одного из аль- тернативных признаков: ЛСДК, ЛСДК, ЛСДК, ЛСДК. Для таких систем су- ществует незначительное число общих методов аналитического исследова- ния; в основном, они разработаны только для частных случаев.

Операторы второго уровня сложности получаются введением двух отрица-

ний: ЛСДК; ЛСДК; ЛСДК; ЛСДК; ЛСДК; ЛСДК.

При трех отрицаниях получаем операторы третьего уровня сложности: ЛСДК; ЛСДК; ЛСДК; ЛСДК.

Операторы четвертого уровня сложности: ЛСДК – нелинейные нестацио-

нарные стохастические бесконечномерные. Им, например, соответствуют нелинейные дифференциальные уравнения в частных производных с переме-

нными случайными параметрами.

Для систем, описываемых операторами второго и выше уровней сложнос-

ти, как правило, имеется только единственная возможность их анализа и син-

теза путем вычислительных экспериментов.

Если модель системы образована элементами различных классов, то класс системы определяется классом элемента с максимальным числом отрицаний.

Автономные системы.

Система называется автономной, если на нее не действуют внешние силы,

в том числе параметрического типа. Автономные системы, таким образом,

стационарны. Изменение их состояния происходит в силу накопленной ранее

энергии. На рис.2.11. модель среды представлена в виде автономной систе-

мы, имеющей выход, но не имеющей входов.

у Рис.2.11. Автономная система

Дифференциальные уравнения автономных систем включают переменные

системы и их производные, но не содержат переменных, описывающих воз-

действия среды и имеют постоянные параметры. Это так называемые одно-

родные дифференциальные уравнения.

Ф(у, у’, у”,….., уⁿ) = 0 , (2 – 11)

дополнительные начальные условия:

у(0), у’(0),….., у^{(n –1)}(0).

Начальные условия являются следствием предыстории системы и вместе с

дифференциальными уравнениями полностью определяют поведение авто-

номной системы. Если система автономна, то ее движение (поведение) на-

зываются свободными.

В случае автономных систем с дискретным временем имеем однородные

разностные уравнения: Ф*(у(k), Dу(k), D²у(k),….,Dⁿу(k)) = 0 (2 – 12)

Модели среды.

Среда на входе системы моделируется автономными системами – генера-

торами воздействий (см. рис.2.11). или преобразователями типовых воздей-

ствий – фильтрами. Распространенными типовыми сигналами, моделирую-

щими детерминированное воздействие, являются единичные импульсная и

ступенчатая функции. Примером типового случайного воздействия является

так называемый “белый шум”.

Среда может моделироваться динамической системой того же класса, что и

сама система управления. Однако часто рассматриваются детерминирован-

ные системы со случайным воздействием на входе.

2.5. Способы построения моделей.

В зависимости от характера и объема априорной информации об объекте

исследования определяют два способа построения моделей систем управле-

ния в формах, принятых в теории управления: 1 – аналитический; 2 – экспе-

риментальный.

Аналитический способ.

Аналитический способ применяется для построения моделей объектов хо-

рошо изученной природы. В этом случае имеется вся необходимая информа-

ция о свойствах объекта и она представлена структурными моделями в виде схем с сосредоточенными компонентами (рис.2.12а).

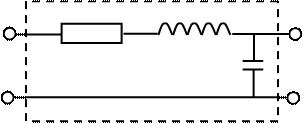
L

R C

а) б)

B K

в)

М

Рис.2.12. Физические системы с сосредоточенными комплектами (а):

электрическая схема (б) и механическая поступательная система (в)

Подобные схемы являются моделями, в которых информация об интересу-

ющих свойствах объекта представлена в наглядной форме с использованием графических образов, отражающих физическую природу явлений, устройства

и параметры объектов. По существу, принципиальные схемы суть стационар-

ные линейные модели с сосредоточенными компонентами (конечномерные),

только представлены они с использованием обозначений, принятых соответ-

ственно в электротехнике и механике.

Методы теории управления абстрагируются от конкретной природы объек-

тов и оперируют более общими- математическими (символьными) моделями.

Аналитический способ моделирования складывается из этапа построения

схемы объекта и ее дальнейшего преобразования в математическое описание

требуемой формы. При этом принципиальные проблемы моделирования ре-

шаются на первом – неформальном этапе. Второй этап, по существу, оказы-

вается процедурой преобразования форм представления модели. Это позво-

ляет разрабатывать различные компьютерные программы, позволяющие ав-

томатизировать составление уравнений по схемам.

Описание вышеуказанных объектов (электрического и механического), т.е.

составления дифференциальных уравнений можно ограничиться классом ли-

нейных стационарных моделей.

Электрическая схема (рис.2.12,б). В ней активными двухполюсниками явля-

ются источник напряжения и источник тока.

Уравнения связи двухполюсников в конкретной схеме выражаются закона-

ми Кирхгофа, представляющими собой условия непрерывности токов и рав-

новесия напряжений: 1 – сумма токов в любом узле равна нулю; 2 – сумма

напряжений в любом контуре равна нулю.

В соответствии с первым законом имеем: i_R = i_L = i_C = i.

Второй закон для единственного контура запишем так: u + u_R + u_C + u_L = 0.

Определим напряжения u_R и u_L через u_C:

u_R = RC duC/dt; u_L = LC d²uC/dt²,

получим дифференциальное уравнение второго порядка:

LC d²uC/dt² + RC duC/dt + u_C = - u.

Механическая поступательная система.