Системы управления с самонастройкой или, в общем случае, с адаптацией

получают информацию об изменениях свойств объекта путем текущей иден-

тификации. Это означает, что каким-либо способом оценивается следствия

параметрических воздействий среды на объект. Текущая информация об от-

клонениях свойств объекта используется для принятия решения о подстрой-

ке параметров управляющих устройств и/или регуляторов (контроллеров). На

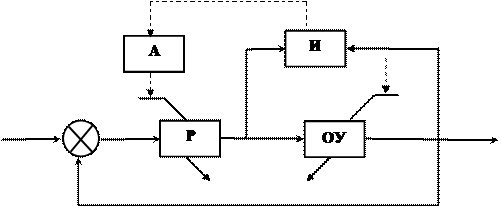
рис.2.7. представлена структура адаптивной (самонастраивающейся) систе-

мы. Следящая система образованная объектом ОУ и регулятором Р, требует

подстройку параметров регулятора из-за изменений свойств объекта. Так как

причины, вызывающие эти изменения, непосредственно нельзя измерять, ос-

тается оценивать их следствие.

В результате текучей информации И путем обработки данных о входе uи

выходе уобъекта оцениваются отклонения его характеристик. На базе этой

информации в блоке адаптации Авычисляются значения параметров регуля-

dQ

dР F

у* u у

Рис.2.7. Адаптивная система управления

тора Р. Здесь реализуется принцип отрицательной (параметрической) обрат-

ной связи – образуется замкнутый контур передачи и обработки информации

для ослабления параметрических возмущений среды.

Следует отметить, что замкнутый основной контур системы, образованный

объектом и регулятором, можно трактовать как объект управления системы более высокого (второго) уровня иерархии. Управляющим воздействием сис-

темы второго уровня являются изменения параметров регулятора первого

уровня, а возмущением – параметрические воздействия среды. Роль измери-

тельного элемента в системе второго уровня играет устройство текущей иде-

нтификации И, а регулятора – блок настройки А. В блоке А по вариациям ха-

рактеристик объекта или отклонениям показателей качества вычисляются па-

раметры регулятора Р, из условий сохранения заданных показателей качества системы нижнего уровня иерархии. Это так называемая самонастраивающая

система управления.

В общем случае целью адаптивной системы является оптимизация показате-

лей качества, т.е. настройка регулятора связана с поиском экстремума неко-

торого функционала.

2.3. Классификация систем управления.

Системы управления классифицируются по: информационному принципу,

типу сигналов, алгоритметрическому и энергетическому признакам.

Вышеизложенный материал посвящен классификации систем управления

по информационному признаку, самому распространенному.

Классификация систем управления по типу сигнала.

Понятия “переменная”, “воздействие”, “сигнал” в теории управления имеют

в основном информационный смысл. Сигналы на входах и выходах функцио-

нальных элементов систем управления рассматриваются как носители инфо-

рмации, а сами элементы – преобразователи сигналов – как устройства пере-

дачи и обработки этой информации.

Если информация кодируется уровнями сигналов – функций непрерывного

времени (рис.2.8,а) – это непрерывние системы (системы с непрерывным вре-

менем, аналоговые системы). Здесь время и уровни всех сигналов принадле-

жат множеству мощности континуума.

Если информация кодируется каким-либо параметром (высота, ширина,

фаза) импульсов определенной формы – это импульсные системы. Различают

импульсные системы с амплитудно-импульсной, широтно-импульсной, фаза-

импульсной модуляциями.

На рис.2.8,б представлена последовательность прямоугольных импульсов,

высота (амплитуда) которых кодирует информацию в моменты времени, кра-

тные периоду Т – это случай амплитудно-импульсной модуляции.

В математических моделях импульсных систем используется понятие дис-

кретного времени, принадлежащего счетному множеству, а параметр импуль-

са – амплитуда - принадлежит множеству мощности континуума. Имеет мес-

то автоматические системы, в которых информация кодируется частотой им-

пульсов

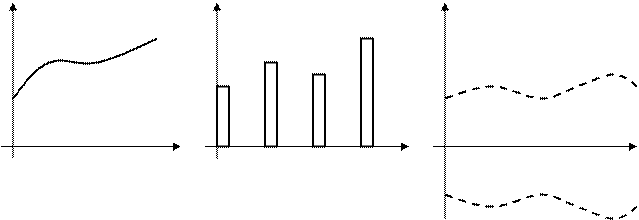у у у

t t t

0 0 T 2T 3T 0

а) б)

Рис.2.8. Типы сигналов в)

В цифровых системах управление как и в импульсных происходит кванто-

вание времени. В силу конечности разрядной сетки вычислительных уст-

ройств имеет место квантование и уровня, т.е. уровень принадлежит конеч-

ному множеству (даже большой мощности).

Важное место занимают системы управления, в которых информация коди-

руется амплитудой переменного тока, т.е. огибающей несущего сигнала. Примерами таких систем являются автоматические системы с двигателями

переменного тока, системы с радиоканалами с амплитудной модуляцией и

другие (рис.2.8,в).

Классификация систем автоматического регулирования по типу алгорит-

ма (закона).

Рассмотрим структуру системы автоматического регулирования с обрат-

ной связью (рис.2.9.). Регулятор Р на базе информации об ошибке е(t), т.е.

отклонении управляемой переменной у(t) от задания у*(t), формирует по

некоторому алгоритму управляющее воздействие u(t) на объект ОУ.

у* е u у

Рис.2.9. Система автоматического регулирования с обратной связью

Используют различные алгоритмы, или законы регулирования. Обозначим

некоторые из них, полагая, что все переменные являются функциями непре-

рывного времени.

Пропорциональный закон (П-закон) регулирования имеет ясную логику – чем больше ошибка, тем сильнее воздействия на объект. Если регулятор трактовать как преобразователь сигналов, то математический алгоритм име-

ет вид: u(t) = k_pe(t) (2 – 2)

Интегральный закон (И-закон) регулирования означает, что уровень воз-

действия на объект определяется суммарной ошибкой, накопившейся за оп-

ределенное время: u(t) = k_I 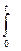e(t)dt + u_o (2 – 3)

Если продифференцировать последнее выражение по времени, получим,

что du(t)/dt = k_Ie(t) ,

т.е. ошибка системы определяет скорость изменения управляющего воздей-

ствия. Характерной чертой И-закона является то,что управляющее воздей-

ствие изменяется до тех пор, пока ошибка не станет равной нулю.

Пропорционально-интегральный закон (ПИ-закон) является комбинацией

двух предыдущих: u(t) = k_pe(t) + k_I 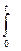e(t)dt (2 – 4)

Пропорционально-интегрально-дифференциальный закон (ПИD-закон)

формирует управляющее воздействие с учетом и скорости изменения

ошибки: u(t) = k_pe(t) + k_I 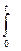e(t)dt + k_Dde(t)/dt (2 – 5)

Этот закон наиболее часто реализуется в системах промышленной авто-

матики.

Классификация систем управления по энергетическому признаку.