Замкнутой САУ называют систему, в которой процесс управления ОУ зависит от результата управления. 12 страница

4. Поскольку система должна быть устойчива, пусть наклон ЛАЧХ на 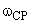будет –20 дБ/дек.

Принятые положения, позволяют описать свойства систем в области низких и высоких частот двумя передаточными функциями:

В области низких частот

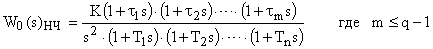
В области высоких частот

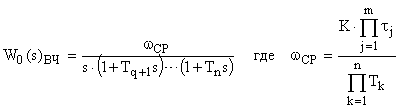
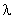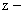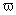Теперь для формального перехода в область псевдочастот (минуя промежуточные и -преобразования) достаточно подставить в передаточной функции 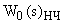вместо 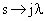и умножить ее на множитель 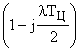, для низких частот приближенно равный 1.

А передаточная функция 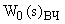будет соответствовать выражение:

,

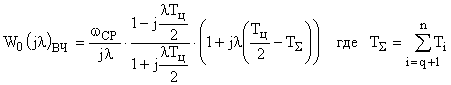Модуль которого:

.

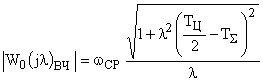Результирующий фазовый сдвиг обеих областей определяется следующим выражением:

.

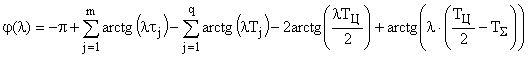Из вышесказанного можно сделать следующие выводы:

1. В области низких частот 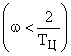асимптотическая ЛАЧХ системы с ЦВМ практически сливается с ЛАЧХ непрерывной части (множитель 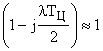) и можно положить 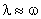. Это позволяет один к одному использовать разработанную для непрерывных систем методику формирования низкочастотной части желаемой ЛАЧХ.

2. В области высоких частот отличия вносит множитель 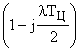, ухудшающий условия устойчивости. Поэтому при формировании запретной высокочастотной области в расчетных формулах величина 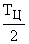должна быть просуммирована с малыми постоянными времени:

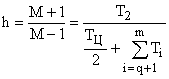
для желаемых частотных характеристик, содержащих 3 участка с наклонами –40, –20 и –40 дб/дек.

,

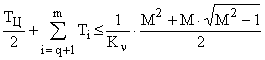где

.

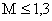Последнее выражение используется для систем, желаемые частотные характеристики имеют два участка с наклонами –20 и –40 дб/дек.

12.3.1. Цифровая коррекция

Цифровая или дискретная коррекция весьма интересна с практической точки зрения в силу конструктивной универсальности устройств и гибкости настройки. Решения задач коррекции предполагают модификации низкочастотного и среднечастотного фрагментов ЛАЧХ, как правило, с уменьшением частоты среза 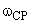. Известно, что в этом диапазоне системы с ЦВМ и их ЛАЧХ — 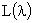не отличаются существенно по свойствам от непрерывных аналогов. Поэтому методика синтеза коррекции едина для цифровых и непрерывных систем. Проектирование же дискретной коррекции ведется в четыре этапа.

1. Синтез передаточной функции непрерывного корректирующего устройства 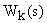по методикам разработанным для непрерывных систем.

2. Переход от непрерывной передаточной функции корректирующего устройства 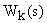к эквивалентной дискретной 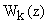посредствам последовательных переходов по изображениям:

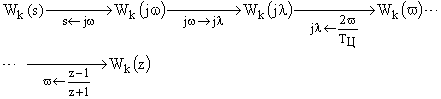
с помощью результирующей формулы билинейного преобразования (т.е. формальной подстановки):

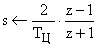
где: 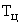— период дискретизации ЦВМ.

3. Составление структурной схемы дискретной передаточной функции 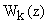, оптимизированной при реализации по объ¨му памяти, быстродействию или для контроля промежуточных фазовых координат системы.

4. Написание программы для ЦВМ (периферийный контроллер, микроЭВМ, ЭВМ, цифровой сигнальный процессор — DSP) или разработка схемы на цифровых микросхемах.

· Заметим, что из непрерывной передаточной функции можно получить бесконечное количество вариантов дискретной передаточной функции, при разных периодах дискретизации ЦВМ (этап 2).

· Обычно частоту дискретизации 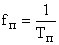выбирают в 6..10 раз больше частоты среза 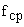разомкнутой системы. Первоначально частоту дискретизации выбирают большой 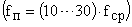, за тем, за две три попытки стремятся ее уменьшить (т.е. повторяют этап 2). При низких частотах дискретизации качество переходного процесса ухудшается настолько (в сравнении с непрерывной коррекцией), что платить за это понижением производительности ЦВМ не представляется возможным. Соответствующую передаточную функцию 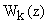используют в дальнейшем.

· При синтезе передаточной функци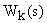и или 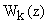необходимо, что бы степень числителя 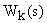не была больше степени знаменателя или свободный коэффициент a₀ в знаменателе передаточной функции 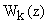не был нулевым, иначе невозможно реализовать программу.

· Если требуется обратный переход от 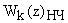к 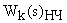следует воспользоваться обратной формулой билинейного преобразования:

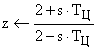
Этот переход однозначен при известном периоде работы ЦВМ .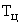

12.3.2. Цифровые регуляторы

В непрерывных системах широко используются пропорционально-интегрально-дифференциальные (ПИД) регуляторы, которые представляются идеализированным уравнением:

,

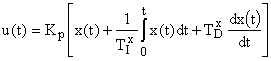где: 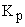— коэффициент усиления пропорционального канала; 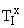— постоянная времени сопрягающего полюса интегрального канала; 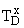— постоянная времени сопрягающего полюса дифференциального канала.

Для малых периодов дискретизации 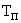уравнение может быть преобразовано в разностное без существенной потери в точности. Непрерывное интегрирование может быть представлено с помощью метода прямоугольников, или метода трапеций.

Метод прямоугольников. Используем этот метод для аппроксимации непрерывного интеграла и запишем ПИД-закон в дискретном виде:

.

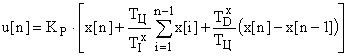В результате получен нерекуррентный (позиционный) алгоритм управления, который требует сохранения всех предыдущих значений сигнала ошибки 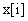, и в котором каждый раз заново вычисляется управляющий сигнал .

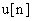Для реализации программ закона регулирования на ЦВМ более удобным является рекуррентный алгоритм. Он характеризуется тем, что для вычисления текущего значения сигнала 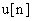используется его предыдущее значение 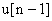и поправочный коэффициент, не требующий существенных вычислительных затрат. Определим его:

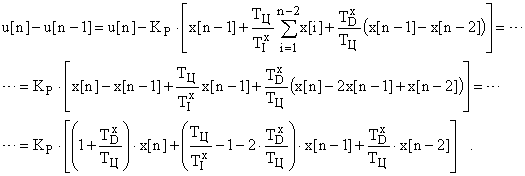
Обозначим в этом выражении:

.

.

.

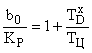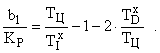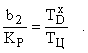Перенесем 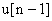в правую часть и получим "скоростной" алгоритм для программной реализации регулятора:

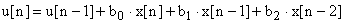
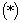
Метод трапеций. Если для аппроксимации непрерывного интеграла использовать метод трапеций, то разностное уравнение будет иметь вид:

.

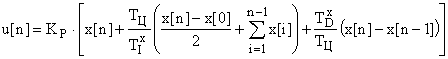Преобразования, аналогичные выше изложенным, при получении рекуррентного соотношения 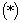, выявляют отличия только для коэффициента :

.

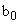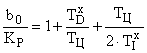Запишем разностное уравнение 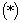для изображений в 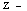домене:

,

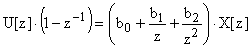и представим его в виде дискретной передаточной функции:

.

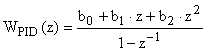Анализ ее коэффициентов показывает, что:

1. Для исключения статической ошибки, передаточная функция должна иметь полюс .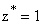

2. Если 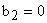, то получим ПИ-регулятор.

3. Если 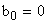, а 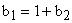, то получим пропорциональнодифференциальный регулятор.

12.3.4. Алгоритмы программ цифровых фильтров

Существует три основных алгоритма программной реализации дискретных передаточных функций ( 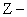передаточных функций):

No алгоритма	Алгоритм	Требуемое быстродействие	Объ¨м памяти
	Непосредственный а) с двумя буферами б) с одним буфером		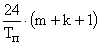9m+9k+12
	Последовательный		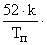20k+10
	Параллельный		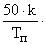19k+8

Дискретную передаточную функцию можно представить в любой из форм:

Алгоритм 1.

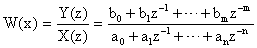— стандартная форма для дискретных передаточных функций.

Алгоритм 2. — разложение 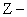передаточных функций на множители

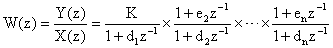
Алгоритм 3. — разложение 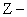передаточных функций на элементарные дроби вида

,

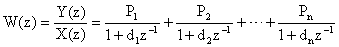где: 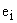— нули z-передаточной функции; 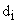— полюса 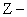передаточной функции; 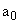— не равно нулю; 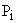— коэффициенты разложения

Этим формам представления z-передаточных функций соответствуют структурные схемы изображенные на рис. 4.

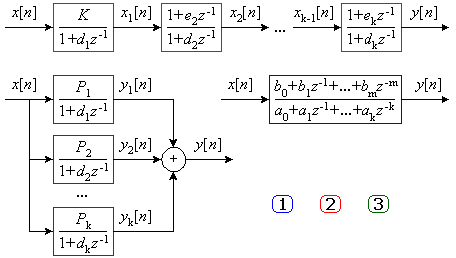
Рис. 4. Варианты построения цифровых фильтров

Разложения по алгоритмам 2 и 3 делают параметры z-передаточных функций независимыми, позволяют контролировать ряд дополнительных фазовых координат: 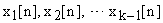; или 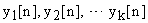— что удобно при отладке систем.

· Последовательная структура алгоритма 2 удобна при синтезе дискретной коррекции.

· Параллельная структура алгоритма 3 удобна для построения цифровых регуляторов.

· Разложение 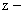передаточных функций на элементарные дроби алгоритма 3 позволяет реализовать 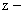передаточных функций на параллельно работающих ЦВМ для повышения быстродействия.

Перечисленные факторы определяют выбор алгоритма программы для ЦВМ.

После разложений, каждый из множителей в форме алгоритма 2 или каждую из элементарных дробей в форме алгоритма 3 следует представить в стандартной форме по алгоритму 1 (с отрицательными степенями оператора z). Переход к разностным уравнениям будет един. 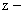передаточную функцию в форме по алгоритму 1 соответствует разностное уравнение вида:

,

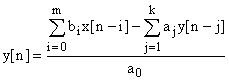по которому и составляется программа. Поскольку текущее значение выходной координаты 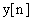рассчитывается по предыдущим значениям 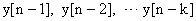— данное разностное уравнение называется рекурсивным.

Изобразим структурную схему цифрового фильтра для этого уравнения (см. рис. 5). Ее можно преобразовать, объединив два буфера (см. рис. 6). Цепочки элементов 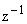в программах будут соответствовать буферам из ячеек памяти, данные в которых сдвигаются на каждом такте дискретизации.

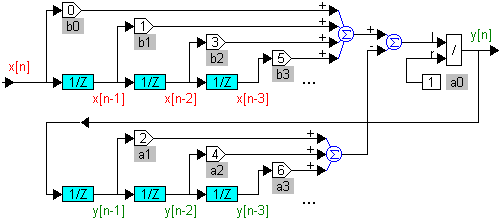
Рис. 5. Структурная схема цифрового регулятора.

Структурной схеме соответствует алгоритм 1. Условие ее физической реализуемости —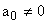

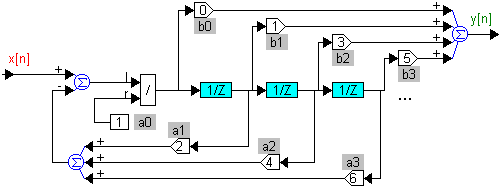
Рис. 6. Преобразованная структурная схема цифрового регулятора.

Если выбран последовательный алгоритм 2 или параллельный алгоритм 3, то структура каждого множителя или элементарной дроби первого порядка (см. рис. 1) будет иметь более простой вид (см. рис. 7).

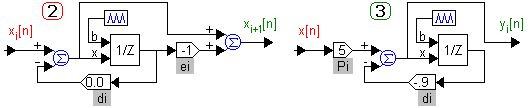
Рис. 7. Схемы цифровых регуляторов по алгоритмам 2 и 3.

Согласно структурной схеме рис. 5, составим процедуру, реализующую дискретную передаточную функцию второго порядка:

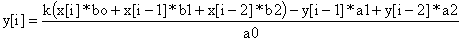
где: 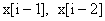и 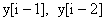— ячейки двух буферов, т.е. регистры задержки — .

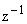По этому уравнению выбираем коэффициенты z-передаточной функции для расчета переходной характеристики и проводится ее построение.

12.4.Об эффекте квантования параметров

Передаточная функция цифрового ПИД-регулятора имеет три коэффициента 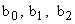. Заметим, что только один коэффициент 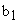содержит информацию о таком параметре регулятора как постоянная времени сопрягающего полюса интегрального канала 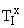. Для объяснения сути эффекта квантования параметров рассмотрим не усугубляющий случай плотного расположения сопрягающих полюсов. Пусть 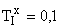; ; 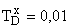при 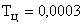. Рассчитаем коэффициент :

.

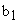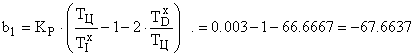Это значение в двоичной форме записи может быть представлено как:

.

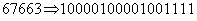Следовательно, мантисса числа, задающего коэффициент 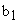должна содержать не менее 17 двоичных разрядов.

Заметим, что для любой системы отклонение любой постоянной времени в два раза не должно иметь критического значения. Однако коэффициенты передаточных функций, как это показано ранее, зависят от параметров отличающихся на порядки. Поэтому для отношения 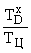, входящего во все коэффициенты числителя передаточной функции регулятора требуется сохранять мантиссу длиной 5 знакомест (17 двоичных разрядов), поскольку иначе информация о параметре 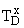будет потеряна вследствие округления.

Существуют следующие методы преодоления эффекта квантования параметров при ограниченной длине мантиссы ЦВМ:

Развязка параметров посредствам разложения z-передаточных функций высокого порядка либо на множители, либо на элементарные дроби.

Подбор для реализации z-передаточных функций структурной схемы среди альтернативных, имеющих разные по плотности сетки возможных положений корней в единичной окружности.