Замкнутой САУ называют систему, в которой процесс управления ОУ зависит от результата управления. 8 страница

Введение новых фазовых координат посредством неособого преобразования 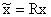приводит к эквивалентным системам различной структуры. При некотором преобразовании может оказаться, что часть управляющих величин не входит в некоторые дифференциальные уравнения (7) или часть фазовых координат не участвует в формирование вектора выходного сигнала . В первом случае система не будет полностью управляемой, а во втором — полностью наблюдаемой.

В случае не полностью управляемой системы ее исходное уравнение могут быть представлены в виде

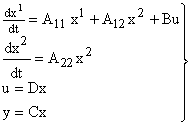
Это иллюстрирует рис. 7. Набор фазовых координат 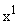соответствует управляемой части фазовых координат, а набор — неуправляемой части.

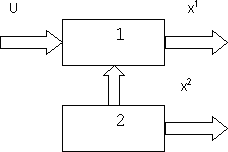
Рис. 7. Пример не полностью управляемой системы

Калманом был доказан критерий управляемости, который гласит, что размерность 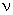управляющей части системы, то есть порядок первой группы уравнений (7) совпадает с рангом матрицы

,

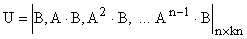где k — размерность управляющего вектора.

При 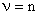система полностью управляема, при — система не полностью управляема, при — система полностью не управляема.

Рис. 8. Структура исходной системы.

На рис. 8 представлен простейший пример. Если рассматривать выходную величину 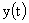при нулевых начальных условиях, то можно записать

,

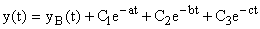где 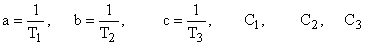определяются начальными условиям до приложения входного сигнал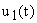а , а 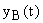— вынужденная составляющая. Система устойчива при .

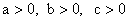Если начальные условия до приложения управляющего сигнала были нулевыми, то поведение системы может быть рассчитано по передаточной функции

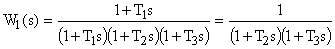
В этом случае переходный процесс в системе определяется как

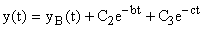
Как следует из последнего выражения, во втором случае система описывается дифференциальным уравнением не третьего, а второго порядка. Система будет устойчивой даже при .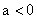

Рассмотренная система будет не полностью управляемой. В ней оказывается 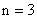, а .

При введении второй составляющей управления 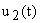система оказывается полностью управляемой, и ей будет соответствовать матрица-строка передаточный функций по управлению

.

В случае не полностью наблюдаемой системы ее уравнения могут быть представлены в виде

.

Эти уравнения отличаются от (7) тем, что фазовые координаты группы не входят ни в выражения для 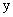и 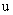, ни в первое уравнение, куда входят фазовые координаты группы 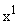. Группа фазовых координат относится к ненаблюдаемым.

Калманом показано, что порядок первой группы уравнений 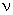совпадает с рангом матрицы V вида

.

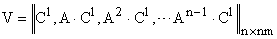При 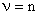система полностью наблюдаема, при — система не полностью наблюдаема, при — система полностью ненаблюдаемая.

На рис. 9 изображен простейший пример. Для него легко показать, что в формировании выхода участвуют только две фазовые координаты из трех.

Рис. 9. Пример не полностью наблюдаемой системы

В общем случае система может содержать четыре группы фазовых координат:

· управляемую, но ненаблюдаемую часть ,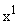

· управляемую и наблюдаемую часть ,

· неуправляемую и ненаблюдаемую часть ,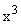

· неуправляемую но наблюдаемую част .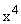

Исходные уравнения системы (7) можно для самого общего случая записать следующим образом:

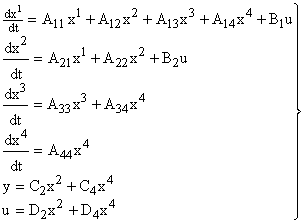
Левая часть характеристического уравнения

,

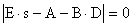где Е — единичная матрица размера 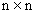, системы в этом случае содержит четыре сомножителя:

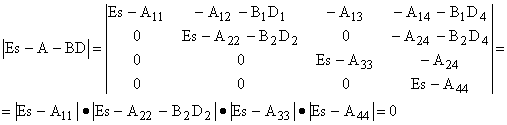
Управляемость и наблюдаемость системы в изложенном смысле не всегда совпадает с практическими представлениями. Даже если какая-либо фазовая координата и может быть вычислена по доступным для измерения выходным величинам обработка измеренных величин может быть, во-первых, сложной и, во-вторых, она может быть затруднена наличием помех. Поэтому практически наблюдаемыми координатами обычно считаются те из них, которые могут быть измерены датчиками различных типов.

Вопросы.

1. Дайте определение устойчивости САУ

2. Какая система автоматического управления называется устойчивой?

3. Какими свойствами обладают нелинейные САУ?

4. Чем определяется устойчивость САУ?

5. Что является математическим признаком устойчивости САУ? Обоснуйте его.

6. Что называется критерием устойчивости САУ?

7. Чем отличаются алгебраические и частотные критерии САУ?

8. Какие критерии устойчивости Вам известны?

9. Критерий устойчивости Гурвица.

10. Критерий устойчивости Рауса.

11. Критерий устойчивости Михайлова.

12. Критерий устойчивости Найквиста.

13. Логарифмический критерий устойчивости.

14. Что вы понимаете под управляемостью САУ?

15. Приведите физический пример интерпретации управляемости САУ.

16. Дайте определение управляемости САУ.

17. Как определить управляемость САУ?

18. Что понимается под наблюдаемостью САУ?

19. Дайте определение наблюдаемости САУ.

20. Как определить наблюдаемость САУ?

21. Что называется САУ с неполной управляемостью? Приведите пример.

22. Как определить наблюдаемость САУ?

Тема. 8. Оценка качества регулирования САУ

Качество любой системы регулирования определяется величиной ошибки:

.

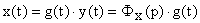Но функцию ошибки 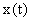для любого момента времени трудно определить, поскольку она описывается с помощью ДУ системы — — высокого порядка, и зависит от большого количества параметров системы. Поэтому оценивают качество САУ по некоторым ее свойствам, определяют которые с помощью критериев качества.

Критериев качества регулирования много. Их разделяют на 4 группы:

Критерии точности — используют величину ошибки в различных типовых режимах.

Критерии величины запаса устойчивости — оценивают удаленность САУ от границы устойчивости.

Критерии быстродействия — оценивают быстроту реагирования САУ на появление задающего и возмущающего воздействий.

Интегральные критерии — оценивают обобщенные свойства САУ: точность, запас устойчивости, быстродействие.

Существует два основных подхода к оценке качества:

Первый использует информацию о временных параметрах системы: ; расположение полюсов и нулей передаточная функция замкнутой системы .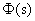

Второй использует информацию о некоторых частотных свойствах системы: полоса пропускания; относительная высота резонансного пика; и т.д.

8.1. Точность в типовых режимах

Для оценки точности используется величина ошибки в различных типовых режимах. Типовые режимы движения состоят в подаче на вход сигналов с нормированными метрологическими характеристиками. Различают следующие типовые режимы изменения задающих сигналов:

· Ненулевое, неподвижное состояние.

· Движение с постоянной скоростью.

· Движение с постоянным ускорением.

· Движение по гармоническому закону.

Рис. 1. Типовые задающие движения.

На рис. 1 показаны режимы: ненулевого, неподвижного положения координаты; движение с постоянной скоростью; движение с постоянным ускорением. Легко понять, что перемещение координаты с постоянной скоростью легко получить интегрированием постоянного сигнала, а для получения координаты движущейся с постоянным ускорением необходимо интегрировать координату, перемещающуюся с постоянной скоростью. Заменив операцию интегрирования оператором, получим изображения по Лапласу.

Ошибки статической системы

Здесь и далее будем рассматривать установившиеся составляющие ошибки системы в типовых режимах ее движения. Для этого будем анализировать уравнение ошибки системы вида:

,

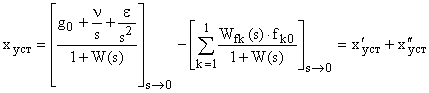где: 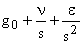— изображение представленного рядом Тейлора входного сигнала; При этом 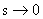соответствует установившемуся режиму.

Итак, пусть передаточная функция САУ 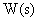является статической, т.е. в области низких частот . Тогда первая составляющая ошибки определяется как:

.

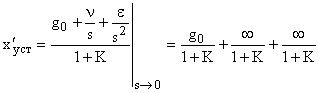Следовательно, в статической системе ошибка, вызванная заданием равным константе, так же константа, но меньшая на величину 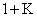, а ошибки от заданий меняющихся с постоянными скоростью, или ускорением нарастают до бесконечности.

Ошибки астатических систем

Если передаточная функция САУ 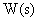обладает астатизмом первого порядка, то в области низких частот 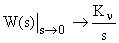. Тогда первая составляющая ошибки определяется как:

.

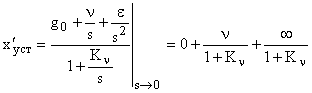Следовательно, в астатической системе первого порядка ошибка от задания равного константе равна нулю, ошибка от задания меняющегося с постоянной скоростью равна 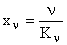, а ошибка от задания, изменяющегося с постоянным ускорением, нарастает до бесконечности.

Если передаточная функция САУ 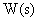обладает астатизмом второго порядка, т.е. в области низких частот 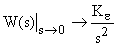. Тогда первая составляющая ошибки:

.

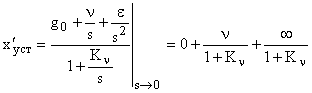Следовательно, в астатической системе второго порядка ошибки от заданий равного константе и изменяющегося с постоянной скоростью равны нулю, а ошибка от задания, меняющегося с постоянным ускорением, равна константе .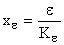

Качество астатических САУ принято характеризовать величинами, называемыми добротностью по скорости и ускорению:

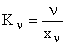и .

Как показано выше астатические САУ не имеют ошибки от постоянных внешних воздействий. Однако это свойство астатических САУ проявляется далеко не всегда. Проанализируем точностные показатели работы астатической САУ при разных точках приложения внешней помехи. Для этого рассмотрим систему, представленную на рис. 2.

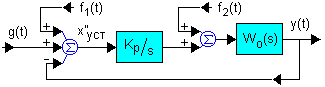
Рис. 2. Астатическая САУ с помехами на входе.

Рассмотрим вторую составляющую ошибки 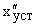от возмущающих воздействий 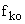. Если САУ астатическая, то 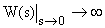, но возможен случай, когда 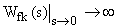. Т.е. при любой степени астатизма САУ 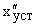может быть отличной от нуля.

.

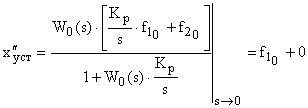Резюме:

Для подавления ошибки от возмущения необходимо, чтобы интегрирующий элемент был включен в контур до места приложения возмущения.

Если рассматривать ошибку чувствительного элемента (сумматора) как возмущение, то, очевидно, что повышение степени астатизма не позволяет устранить ее.

Ошибка при движении по гармоническому закону

Рассмотрим только первую составляющую ошибки:

где:: — синусоида; — комплексное число

Следовательно:

(1)

Резюме:

Формула (1) позволяет идентифицировать положение неизвестной ЛАЧХ на данной частоте по амплитуде ошибки или сформулировать требования к ЛАЧХ при синтезе системы.

Особые точки ЛАЧХ определены комплексными сопряженными корнями. Поведение системы при данных частотах требует дополнительного исследования.

Особенность движения системы при гармоническом сигнале задания — это смена знака координат, которое во многих системах может сопровождаться нелинейными искажениями типа "ступенька" или сменой направления сил сухого трения.

8.2. Коэффициенты ошибок

Пусть известна передаточная функция по ошибке 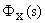, тогда:

где: 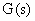— изображение функции .

Разложим 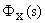в ряд Тейлора:

.

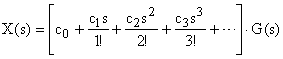(2)

Переходя к оригиналу получаем:

.

Величины 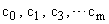— называют коэффициентами ошибок. Их можно определять двумя способами:

.

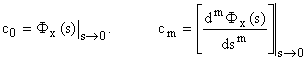Делением числителя 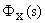на знаменатель и сравнением с рядом (2).

Примечание:

Коэффициенты ряда (2) непосредственно связанны с коэффициентом усиления САУ, добротностями ,...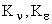

Система \ Ошибки

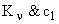
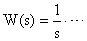
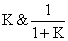
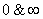
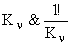
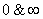
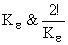
САУ астатическая сигналу задания может быть статической для 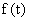, поэтому равенство нулю коэффициентов 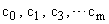для сигнала не обязательно означает равенство нулю коэффициентов 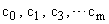для сигнала .

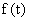Ограничение количества членов ряда (2) и предположение о постоянстве коэффициентов ошибок 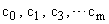определяет применение метода для плавно меняющихся сигналов и 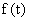, когда переходная составляющая в движении системы успевает затухнуть.

8.3. Оценка запаса устойчивости и быстродействия по переходной характеристике

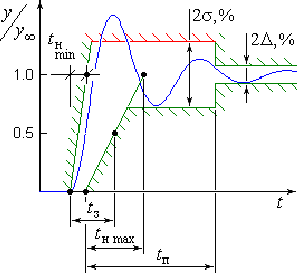
Рис. 3. Переходная характеристика САУ.

Для оценки качественных показателей работы САУ в динамических режимах анализируется ее реакция на ступенчатое единичное воздействие (рис. 3). При этом переходная характеристика должна находиться в пределах заданной области, параметры которой определяются требования технологического агрегата. Исходя из параметров переходной характеристики, можно определить реальные запасы устойчивости САУ по модулю и фазе. Переходная характеристика оценивается совокупностью параметров, которые называются показателями качества. К ним относятся:

перерегулирование – отношения максимального отклонения управляемой переменной относительно ее установившегося значения в направлении, противоположном начальному отклонению;

колебательность 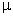— число максимумов или минимумов переходной характеристики за время регулирования;

длительность переходного процесса 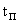– это время, по истечении которого, отклонение управляемой переменной относительно установившегося значения становится и остается по абсолютной величине меньше заданного значения , определяемого требованиями, предъявляемым к САУ;

время достижения первого максимума 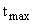– момент времени, в который управляемая переменная достигает своего максимального значения;

время установления 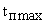– промежуток времени по окончании которого управляемая переменная в первый раз достигает своего установившегося значения;

частота собственных колебаний САУ.

1. Запас устойчивости САУ оценивают по величине перерегулирования:

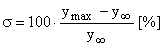
В табл. 1 приведены зависимости значения запаса устойчивости САУ по фазе и колебательности системы в зависимости от величины перерегулирования.

Табл. 1.

Варианты	0 %	10..30 %	50..70 %
Применяемость	редко	часто	избегают
Запас по фазе
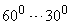
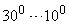
Число колебаний		1, 2	3, 4,...

2. Быстродействие САУ оценивают по времени окончания переходного процесса 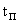, при заданной допустимой ошибке (трубке):

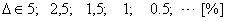
от 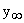, — установлено ГОСТ-ами.

3. Частоту единичного усиления разомкнутой системы можно оценить по частоте колебаний переходной функции.

Примечание: При синтезе САУ используют область допустимых отклонений регулируемой величины.

Время нарастания выходной координаты САУ ограничено:

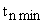- допустимым ускорением координат и предельными колебательными режимами;

- требуемым быстродействием.

8.3. Корневые методы оценки качества

Поскольку корни передаточной функции САУ, а точнее ее характеристического полинома, однозначно определяют вид переходного процесса, их можно использовать для оценки:

запаса устойчивости,

быстродействия.

Обычно обходятся исследованием только полюсов передаточная функция, т.е. корней характеристического уравнения.

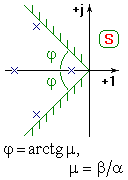
Рис. 4. Распределение корней передаточной функции.

На рис. 4 показано распределение нескольких корней передаточной функции САУ. Следует отметить, что, если имеются комплексные корни вида - 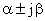, то система будет склонна к колебаниям. Оценить эту склонность можно используя показатель запаса устойчивости — колебательность. Колебательность определяется как:

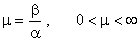
где: 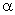— коэффициент затухания; — круговая частота колебаний.

Колебательность определяет другой показатель — затухание амплитуды колебаний за период частоты собственных колебаний САУ.:

.

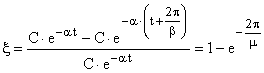То есть

.

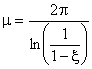Задание определенной колебательности, ограниченной требованиями технологического агрегата, ограничивает допустимую область расположения корней.

Колебательность системы 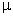можно найти, используя подстановку 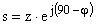, что соответствует повороту осей плоскости корней на угол 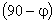. Далее, используя любой критерий устойчивости, подбирают угол , при котором система будет находиться на границе устойчивости. И тогда:

Для оценки быстродействия САУ может использоваться понятие степени быстродействия 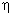то есть абсолютного значения вещественной части ближайшего к мнимой оси корня. Следовательно, если этот корень 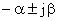, то 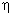равна коэффициенту затухания .

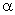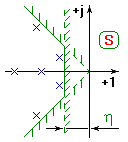
Рис. 5. Допустимые области расположения корней характеристического полинома.

И действительно, составляющая в переходном процессе , затухает тем медленней, чем меньше 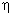. Если в конце переходного процесса амплитуда колебаний равна 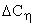, то время переходного процесса: