Замкнутой САУ называют систему, в которой процесс управления ОУ зависит от результата управления. 7 страница
Определение: чтобы САУ была устойчива, необходимо и достаточно, чтобы определитель Гурвица и его диагональные миноры имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения замкнутой САУ. При 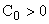 для устойчивости САУ необходимо и достаточно выполнение условий:
для устойчивости САУ необходимо и достаточно выполнение условий:
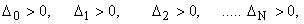 ;.
;.
Рассмотрим замкнутую САУ, состоящую из трех последовательно включенных апериодических звеньев, охваченных 100% обратной связью.
Передаточная разомкнутой САУ функция имеет вид:
 .
.
Передаточная функция замкнутой САУ определяется как
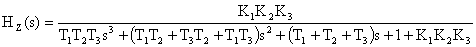 .
.
Главный определитель Гурвица имеет вид:
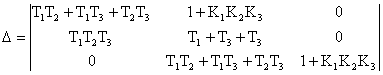 .
.
Первый определитель Гурвица  . Это условие выполняется для всех возможных комбинаций параметров САУ.
. Это условие выполняется для всех возможных комбинаций параметров САУ.
Второй определитель Гурвица определяется как
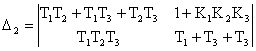 .
.
Раскрывая определитель получаем
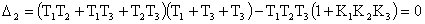 .
.
Решая это уравнение относительно суммарного коэффициента усиления САУ 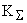 , определяемого как
, определяемого как
 ,
,
получаем, что
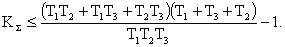
Из этого следует, что суммарный коэффициент усиления САУ не может превышать некоторую величину. Следовательно, пределы уменьшения погрешности стабилизации регулируемой координаты в такой системе ограничены.
7.2.2. Алгебраический критерий Рауса.
Этот критерий представляет собой систему неравенств, составленных по особым правилам из коэффициентов характеристического уравнения замкнутой САУ.
В первой строке таблицы записывают коэффициенты характеристического уравнения, имеющие четные индексы в порядке их возрастания. Во второй строке таблицы записывают коэффициенты с нечетными индексами в порядке их возрастания. В последующие строки вписывают коэффициенты, определяемые как
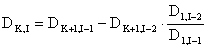 ,
,
где – i – индекс, обозначающий номер строки таблицы,
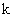 – индекс, обозначающий номер столбца таблицы. Число строк таблицы Рауса на единицу превышает порядок характеристического уравнения замкнутой САУ.
– индекс, обозначающий номер столбца таблицы. Число строк таблицы Рауса на единицу превышает порядок характеристического уравнения замкнутой САУ.
Условия устойчивости Рауса: Чтобы САУ была устойчивой необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Рауса имели один и тот же знак, то есть были положительными. Если не все коэффициенты первого столбца таблицы Рауса положительны, то есть САУ неустойчива, число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса.
7.2.3. Частотный критерий Михайлова.
Критерий Михайлова – это частотный критерий, позволяющий судить об устойчивости замкнутой системы по поведению ее характеристического вектора на комплексной плоскости. Характеристический вектор получают путем подстановки в выражение для характеристического полинома
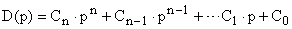 ,
,
Значения 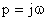 . Тогда характеристический вектор представляется комплексной величиной, определяемой как:
. Тогда характеристический вектор представляется комплексной величиной, определяемой как:
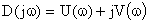 ,
,
где
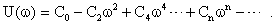
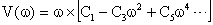
Если задаваться различными значениями 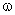 и откладывать значения
и откладывать значения 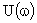 по горизонтальной, а
по горизонтальной, а  – по вертикальной осям декартовой системы координат, то будет получена кривая, называемая годографом характеристического вектора или годографом Михайлова. Другая формулировка: годографом Михайлова называется множество точек, образованных при движении характеристического вектора САУ при изменении частоты от 0 до
– по вертикальной осям декартовой системы координат, то будет получена кривая, называемая годографом характеристического вектора или годографом Михайлова. Другая формулировка: годографом Михайлова называется множество точек, образованных при движении характеристического вектора САУ при изменении частоты от 0 до 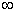 .
.
То есть для устойчивости САУ необходимо выполнение условия вида:
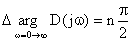 .
.
Для вывода этого утверждения представим характеристический полином в виде
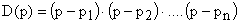 ,
,
где  – корни характеристического уравнения
– корни характеристического уравнения 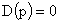 .
.
На комплексной плоскости каждому корню соответствует определенная точка. Подставив 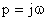 , получаем
, получаем
 .
.
Каждый вектор 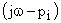 может быть представлен в виде вектора, начало которого лежит в точке, определяющей корень
может быть представлен в виде вектора, начало которого лежит в точке, определяющей корень  а конец лежит на мнимой оси. Следовательно,
а конец лежит на мнимой оси. Следовательно, 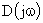 можно представить суммарным вектором, равным произведению элементарных векторов. Модуль суммарного вектора будет равен произведению модулей отдельных векторов, а фаза – сумме фаз этих векторов. При изменении частоты конец каждого вектора будет перемещаться вдоль мнимой оси. При изменении частоты от
можно представить суммарным вектором, равным произведению элементарных векторов. Модуль суммарного вектора будет равен произведению модулей отдельных векторов, а фаза – сумме фаз этих векторов. При изменении частоты конец каждого вектора будет перемещаться вдоль мнимой оси. При изменении частоты от 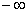 до
до  каждый составляющий вектор, начало которого лежит на вещественной оси, повернется на угол, равный
каждый составляющий вектор, начало которого лежит на вещественной оси, повернется на угол, равный 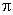 , если его начало лежит в левой полуплоскости, и равный –
, если его начало лежит в левой полуплоскости, и равный – 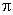 , если его начало лежит в правой полуплоскости. Каждая пара комплексно-сопряженных корней – соответственно на угол +
, если его начало лежит в правой полуплоскости. Каждая пара комплексно-сопряженных корней – соответственно на угол + 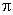 .
.
Если характеристическое уравнение имеет m корней в правой полуплоскости, то в левой полуплоскости число этих корней будет равно n-m. При изменении частоты от 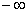 до
до  суммарный угол поворота вектора характеристического полинома определяется как
суммарный угол поворота вектора характеристического полинома определяется как
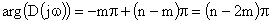 .
.
Для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения лежали в левой полуплоскости, то есть чтобы 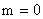 . Таким образом, если вектор характеристического полинома замкнутой САУ порядка "n" при изменении частоты от
. Таким образом, если вектор характеристического полинома замкнутой САУ порядка "n" при изменении частоты от 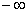 до
до  описывает в положительном направлении угол n
описывает в положительном направлении угол n 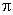 , то такая система регулирования будет устойчива. В противном случае САУ будет неустойчива.
, то такая система регулирования будет устойчива. В противном случае САУ будет неустойчива.
В силу симметричности кривой, описываемой концом вектора характеристического полинома, можно ограничиться рассмотрением лишь ее части, соответствующей положительным значениям частоты. При этом угол, описываемый вектором характеристического полинома при изменении частоты от 0 до  , уменьшится вдвое и будет определяться как
, уменьшится вдвое и будет определяться как
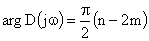 .
.
Формулировка критерия: для устойчивости системы необходимо и достаточно, чтобы ее характеристический вектор при изменении частоты от 0 до  повернулся в положительном направлении (против часовой стрелки), начиная с положительной вещественной оси на число квадрантов, равное порядку характеристического уравнения.
повернулся в положительном направлении (против часовой стрелки), начиная с положительной вещественной оси на число квадрантов, равное порядку характеристического уравнения.
На рис. 3 приведены годографы Михайлова для устойчивых и неустойчивых САУ. Изменение коэффициента 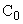 вызывает сдвиг годографа Михайлова вдоль горизонтальной оси без его деформации. Это дает возможность оценить предельное значение этого коэффициента, при котором сохраняются условия устойчивой работы САУ.
вызывает сдвиг годографа Михайлова вдоль горизонтальной оси без его деформации. Это дает возможность оценить предельное значение этого коэффициента, при котором сохраняются условия устойчивой работы САУ.
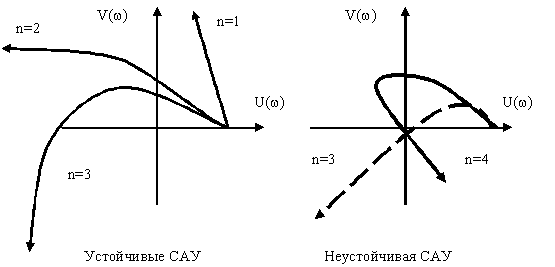
Рис. 3. Годографы Михайлова для устойчивых и неустойчивых САУ
7.2.4. Частотный критерий Найквиста.
Критерий Найквиста – это частотный критерий, позволяющий судить об устойчивости САУ, замкнутой единичной обратной связью, по виду амплитудно-фазовой частотной характеристики разомкнутой системы.
Для формулировки критерия рассмотрим САУ, которая в разомкнутом состоянии характеризуется передаточной функцией вида
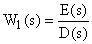 ,
,
где  – некоторые полиномы от
– некоторые полиномы от  , причем степень знаменателя выше или равна степени числителя.
, причем степень знаменателя выше или равна степени числителя.
Знаменатель этого выражения является характеристическим полиномом разомкнутой САУ. Передаточная функция такой системы, охваченной 100% отрицательной обратной связи, определяется как
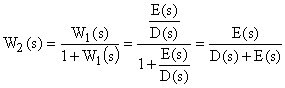 ,
,
где 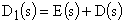 – характеристический полином замкнутой систем.
– характеристический полином замкнутой систем.
Обратное этому выражение определяется как
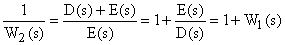 .
.
Обозначим корни характеристического уравнения разомкнутой системы –  .
.
Корни характеристического уравнения замкнутой системы обозначим как — 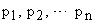 .
.
В плоскости корней, каждый корень может быть представлен вектором, проведенным из начала координат. Если выбрать значение независимой переменной 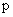 в произвольной точке комплексной плоскости, то комплексное число вида
в произвольной точке комплексной плоскости, то комплексное число вида  может быть представлено в виде разностного вектора, как показано на рис. 4.
может быть представлено в виде разностного вектора, как показано на рис. 4.
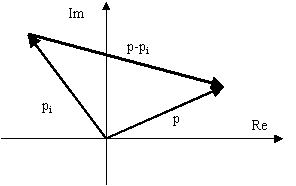
Рис. 4. Графическое представление разности векторов
Если 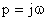 , то разностный вектор будет иметь свое начало в точке окончания вектора
, то разностный вектор будет иметь свое начало в точке окончания вектора  , а окончание – на мнимой оси. В этом случае выражение для обратной передаточной функции замкнутой САУ можно представить как
, а окончание – на мнимой оси. В этом случае выражение для обратной передаточной функции замкнутой САУ можно представить как
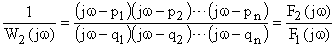
При изменении частоты от 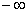 до
до  будет скользить по мнимой оси и повернется на угол
будет скользить по мнимой оси и повернется на угол 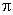 . Поворот будет происходить против часовой стрелки, если корень лежит слева от мнимой оси, и по часовой стрелке, если корень расположен в правой полуплоскости. Числитель и знаменатель этого выражения могут быть представлены как некоторые вектора, модуль которых равен произведению модулей сомножителей, а угол поворота – как сумма углов поворота векторов сомножителей. Поэтому можно записать, что
. Поворот будет происходить против часовой стрелки, если корень лежит слева от мнимой оси, и по часовой стрелке, если корень расположен в правой полуплоскости. Числитель и знаменатель этого выражения могут быть представлены как некоторые вектора, модуль которых равен произведению модулей сомножителей, а угол поворота – как сумма углов поворота векторов сомножителей. Поэтому можно записать, что
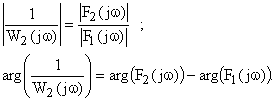
Таким образом полный угол поворота рассматриваемого вектора при изменении частоты от 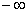 до
до  равен разности углов поворота векторов
равен разности углов поворота векторов  и
и 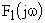 . Для САУ устойчивой в разомкнутом состоянии все корни характеристического полинома лежат в левой полуплоскости. Поэтому суммарный угол поворота вектора знаменателя при изменении частоты от
. Для САУ устойчивой в разомкнутом состоянии все корни характеристического полинома лежат в левой полуплоскости. Поэтому суммарный угол поворота вектора знаменателя при изменении частоты от 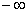 до
до  равен n
равен n 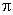 .
.
В общем случае характеристический полином замкнутой САУ имеет 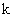 корней в правой полуплоскости и
корней в правой полуплоскости и 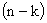 корней в левой полуплоскости. Поэтому суммарный угол поворота вектора числителя при изменении частоты от
корней в левой полуплоскости. Поэтому суммарный угол поворота вектора числителя при изменении частоты от 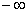 до
до  равен
равен 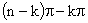 или
или  . Суммарный угол поворота вектора
. Суммарный угол поворота вектора 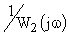 будет определяться как
будет определяться как
 .
.
Для устойчивой САУ все корни характеристического полинома должны располагаться в левой полуплоскости, то есть  . Следовательно суммарный угол поворота вектора устойчивой системы при рассмотренных ранее условиях равен нулю. То есть будет выполняться условие
. Следовательно суммарный угол поворота вектора устойчивой системы при рассмотренных ранее условиях равен нулю. То есть будет выполняться условие
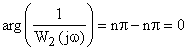 .
.
При выполнении этого условия вектор 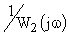 будет располагаться справа от мнимой оси. Этот вектор определяется АФЧХ разомкнутой САУ, но его начало находится в точке (–1,j0). Исходя из этого, формулируется критерий устойчивости Найквиста.
будет располагаться справа от мнимой оси. Этот вектор определяется АФЧХ разомкнутой САУ, но его начало находится в точке (–1,j0). Исходя из этого, формулируется критерий устойчивости Найквиста.
Формулировка критерия. САУ устойчива в замкнутом состоянии, если годограф АФЧХ устойчивой разомкнутой системы не охватывает точки с координатами (-1, j0) на комплексной плоскости. Эта формулировка справедлива как для статических, так и астатических САУ, то есть систем, характеристическое уравнение которых содержит нулевой корень той или иной степени кратности.
На рис. 5 приведены АФЧХ устойчивых и неустойчивых САУ.
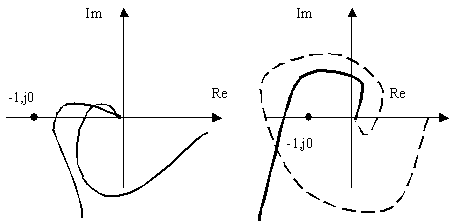
Устойчивые САУ Неустойчивые САУ
Рис. 5. АФЧХ устойчивых и неустойчивых САУ
7.2.5. Логарифмический частотный критерий.
Логарифмический критерий – это частотный критерий, позволяющий судить об устойчивости замкнутой САУ по виду логарифмической характеристики разомкнутой системы. Этот критерий основан на однозначной связи ЛФЧХ и АФЧХ систем автоматического управления. При этом рассматриваются САУ, базирующиеся на использовании устойчивых разомкнутых систем. Кроме того, рассматриваются системы с астатизмом не выше второго порядка.
Как следует из критерия устойчивости Найквиста в устойчивых САУ фазовый сдвиг может достигать значения 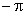 только при модулях комплексной передаточной функции, меньшем чем единица. Это позволяет легко определить устойчивость по виду ЛАЧХ и ЛФЧХ.
только при модулях комплексной передаточной функции, меньшем чем единица. Это позволяет легко определить устойчивость по виду ЛАЧХ и ЛФЧХ.
Формулировка критерия: для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы в диапазоне частот, где ЛАЧХ разомкнутой системы 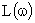 больше нуля число переходов фазовой характеристики
больше нуля число переходов фазовой характеристики 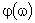 прямой
прямой 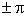 снизу верх превышало на
снизу верх превышало на 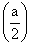 число переходов сверху вниз, где а – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.
число переходов сверху вниз, где а – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.
В частном случае для устойчивой разомкнутой системы (а=0) необходимым и достаточным условием замкнутой системы является необходимость выполнения следующего условия. В диапазоне частот, где 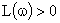 , фазовая частотная характеристика не должна пересекать прямой
, фазовая частотная характеристика не должна пересекать прямой 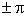 , или пересекать ее одинаковое число раз снизу вверх и сверху вниз.
, или пересекать ее одинаковое число раз снизу вверх и сверху вниз.
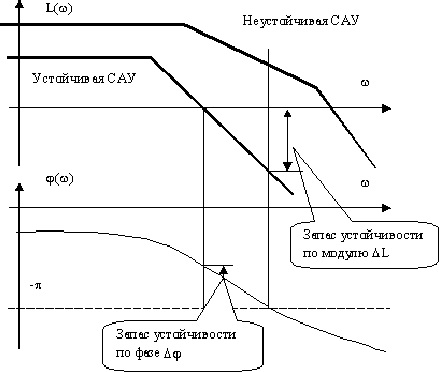
Рис. 6. ЛФЧХ устойчивой и неустойчивой САУ
Критическим значением коэффициента преобразования называется такое его значение, при котором АФЧХ проходит через точку (-1, j0) и система находится на границе устойчивости.
Запасом по модулю называется величина в децибеллах, на которую нужно изменить коэффициент преобразования САУ, чтобы привести ее к границе устойчивости.
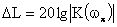 ,
,
где 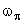 — частота, при которой фазовая характеристика равна
— частота, при которой фазовая характеристика равна 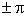 .
.
Запасом устойчивости по фазе называется угол, на который нужно повернуть амплитудно-фазовую характеристику разомкнутой системы, чтобы замкнутая САУ оказалась на границе устойчивости.
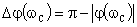 ,
,
где  – значение ФЧХ на частоте среза системы, для которой выполняется условие
– значение ФЧХ на частоте среза системы, для которой выполняется условие  .
.
7.3. Понятие об управляемости системы и ее наблюдаемости.
Рассмотрим случай, когда все переменные состояния могут быть измерены, а результаты этих действий могут быть использованы для управления системой. Однако такой случай не всегда технически реализуем. Поэтому для систем автоматического управления вводится понятие управляемости.
Рассмотрим линейную систему с постоянными коэффициентами:
 , ,
| (1) |
где 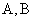 – матрицы с постоянными коэффициентами.
– матрицы с постоянными коэффициентами.
При этом управление полагается скалярным, т.е. управление объектом осуществляется по одной координате.
Заданы начальная и конечная точка 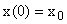 , и
, и  . Задача состоит в том, чтобы перевести систему из заданного начального положения в некоторую точку, совпадающую с началом координат. При этом никаких ограничений на величину управляющего воздействия и время регулирования не накладывается. Если такая задача решается при любых начальных и конечных условиях, то такая система является управляемой.
. Задача состоит в том, чтобы перевести систему из заданного начального положения в некоторую точку, совпадающую с началом координат. При этом никаких ограничений на величину управляющего воздействия и время регулирования не накладывается. Если такая задача решается при любых начальных и конечных условиях, то такая система является управляемой.
Система называется управляемой, если существует такое управление, которое из любого начального состояния в любое конечное положение. При каких условиях система является управляемой. Попытаемся выяснить причины неуправляемости. Это удобно сделать с помощью геометрического представления движения системы. Как отмечалось выше решение линейного однородного уравнения имеет вид:
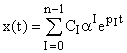
Если какой-нибудь из коэффициентов  , а остальные отличны от нуля, то движение происходит в инвариантном подпространстве матрицы
, а остальные отличны от нуля, то движение происходит в инвариантном подпространстве матрицы 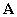 . С геометрической точки зрения все траектории лежат в плоскости S, т.е. вектор
. С геометрической точки зрения все траектории лежат в плоскости S, т.е. вектор 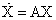 также направлен вдоль этой плоскости. Предположим, что вектор
также направлен вдоль этой плоскости. Предположим, что вектор 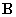 тоже лежит в плоскости
тоже лежит в плоскости 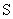 . Очевидно, что добавка к вектору
. Очевидно, что добавка к вектору 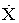 величины
величины  оставляет вектор
оставляет вектор 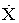 в той же плоскости, хотя и деформирует траекторию движения вектора состояния. Следовательно, если начальная точка лежит в плоскости
в той же плоскости, хотя и деформирует траекторию движения вектора состояния. Следовательно, если начальная точка лежит в плоскости 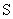 , а конечная — нет, то попасть в точку с заданными координатами нельзя, так как не существует управления, которое переводит состояние системы с заданными параметрами из начальной точки в конечную. Такая система неуправляема по определению.
, а конечная — нет, то попасть в точку с заданными координатами нельзя, так как не существует управления, которое переводит состояние системы с заданными параметрами из начальной точки в конечную. Такая система неуправляема по определению.
Условия управляемости в терминах исходной системы получены Калманом и имеют вид:
Для управляемости системы (1) необходимо и достаточно, чтобы выполнялось условие вида
 . .
| (2) |
Это условие выполняется, если матрица U вида

имеет ранг, равный N.
Рангом матрицы называется наибольший порядок ее определителя, отличный от нуля.
Рассмотрим поведение системы в пространстве состояний собственных векторов  матрицы А (для простоты будем полагать, что собственные значения матрицы А — действительные и различные). Как мы убедимся в дальнейшем, в этом пространстве условия управляемости становятся практически очевидными. Введем неособое преобразование вида
матрицы А (для простоты будем полагать, что собственные значения матрицы А — действительные и различные). Как мы убедимся в дальнейшем, в этом пространстве условия управляемости становятся практически очевидными. Введем неособое преобразование вида
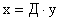 , ,
| (3) |
где 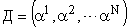 .
.
Выше отмечалось, что 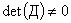 и
и 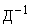 существует. Поэтому вектора X и Y связаны однозначной зависимостью. Следовательно, задачи об управляемости в пространствах этих переменных эквивалентны.
существует. Поэтому вектора X и Y связаны однозначной зависимостью. Следовательно, задачи об управляемости в пространствах этих переменных эквивалентны.
В пространстве новых переменных 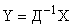 поведение САУ описывается уравнением
поведение САУ описывается уравнением
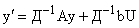 . .
| (4) |
Рассмотрим произведение 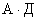
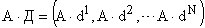 .
.
так как  , то
, то
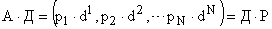 ,
,
где
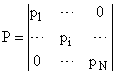
Следовательно, уравнение (4) приводится к виду
 .
.
или
 . .
| (5) |
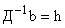 — вектор столбец с компонентами
— вектор столбец с компонентами 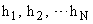 .
.
Так как матрица Р диагональная, то
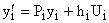 , где
, где 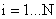 .
.
и если хотя бы одно 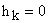 , то координата
, то координата 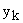 — неуправляема. Поэтому можно предположить, что, если все
— неуправляема. Поэтому можно предположить, что, если все 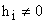 , то система управляема.
, то система управляема.
Рассмотрим n-мерное пространство состояния Х, в котором каждому состоянию системы соответствует некоторое положение изображающей точки, определяемое значениями фазовых координат 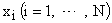 .
.
Пусть в пространстве состояния заданы два множества 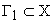 и
и  . Рассматриваемая система будет управляемой, если существует такое управление
. Рассматриваемая система будет управляемой, если существует такое управление 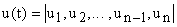 , определенное на конечном интервале времени
, определенное на конечном интервале времени 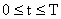 , которое переводит изображающую точку в пространстве Х из подобласти
, которое переводит изображающую точку в пространстве Х из подобласти  в подобласть
в подобласть 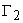 .
.
Можно сузить определение управляемости и понимать под ней возможность перевода изображающей точки из любой области пространства состояний Х в начало координат. Система будет управляемой, если каждое состояние управляемо в этом смысле.
От пространства состояний Х перейдем к другому пространству 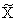 посредством неособого преобразования
посредством неособого преобразования 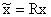 , причем
, причем 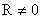 , где
, где 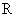 — матрица коэффициентов
— матрица коэффициентов 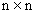 .
.
Тогда вместо уравнения вида
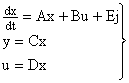 , ,
| (6) |
где j — матрица возмущающих и задающих воздействий,
u — матрица-столбец управляющий величин,
y — матрица-столбец регулируемых величин,
x- матрица-столбец фазовых координат,
будем иметь
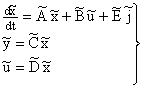 . .
| (7) |
Здесь использованы преобразованные матрицы коэффициентов:
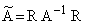 ,
, 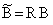 ,
, 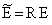 ,
, 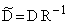 и
и  .
.
Дата добавления: 2015-12-29; просмотров: 1837;
