Замкнутой САУ называют систему, в которой процесс управления ОУ зависит от результата управления. 10 страница

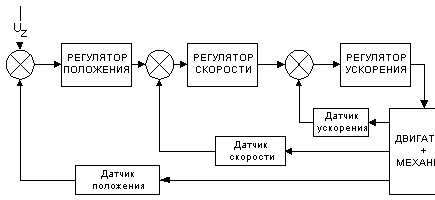
Рис. 3. Блок-схема многоконтурной системы управления

1. Система образуется из нескольких контуров регулирования, число которых равно числу регулируемых параметров. В каждом контуре имеется выходное звено или собственно объект регулирования, а также регулятор. Каждый регулятор содержит в себе ядро, реализующее выбранный способ управления. В состав ядра входят усилитель и последовательное корректирующее устройство, предназначенное для улучшения динамических свойств создаваемого контура регулирования.

2. Контуры регулирования соединяются последовательно, образуя взаимосвязанную многоконтурную систему. Отдельные контуры соединяются таким образом, что выходное напряжение регулятора каждого контура регулирования служит задающим напряжением для контура, являющегося внутренним по отношению к рассматриваемому контуру.

На входе каждого регулятора сравниваются два воздействия: задающее, пропорциональное заданному значению регулируемой величины, и сигнал обратной связи, пропорциональный действительному значению этой величины.

Выходной сигнал регулирования первого самого внутреннего контура служит для выработки регулирующего воздействия на объект регулирования электропривода.

Задачей внутреннего контура является создание наиболее благоприятных условий для выполнения комплекса требований, предъявляемых к внешнему контуру управления. Такие условия возникают при расширении полосы пропускания замкнутого внутреннего контура регулирования. Поэтому целесообразно выбирать структуру и значения параметров регулятора из условия максимизации полосы пропускания замкнутого контура при обеспечении требуемых запасов устойчивости этого контура. В качестве основных факторов, препятствующих решению этой задачи, выступают нестабильность свойств элементов и нелинейность их характеристик, а также не поддающиеся компенсации малые постоянные времени реальных устройств неизменяемой части электропривода.

3. При построении контура регулирования ускорения наиболее просто реализуются связи не по ускорению, а по моменту двигателя, который пропорционален току в якорной цепи электродвигателя. Замена связи по ускорению связью по току широко используется, поскольку ускорение определяется главным образом моментом, развиваемым двигателем, однако эти связи не эквивалентны. В результате такого упрощения образуется контур регулирования момента, который для электродвигателя превращается в контур регулирования тока его якорной цепи.

При таком соединении внутренние контуры оказываются подчиненными внешним контурам регулирования. При этом объект регулирования 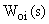какого-либо i-го контура оказывается состоящим из выходного звена данного контура 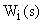, то есть собственно объекта, и замкнутого(i-1)-го контура регулирования, внутреннего по отношению к данному контуру.

Главным в системе является параметр самого внешнего контура регулирования, так как он определяет основную цель автоматического регулирования. Остальные параметры вспомогательные и подчинены главному. Кроме того, вспомогательные параметры также находятся в подчинении один другому.

4. Под оптимизацией контура понимают выбор типа регулятора и настройку параметров последнего таким образом, чтобы наилучшим образом удовлетворялись технические требования с учетом ограничений в электрической и механической частях привода (перегрузочная способность двигателей, их нагрев, допустимая по условиям коммутации на коллекторе скорость нарастания тока, величины ускорений и ударов, допускаемых конструкцией механизмов и т.п.).

5. Способ подчиненного регулирования позволяет легко осуществить ограничение любого параметра, а также относительно просто рассчитать и настроить систему так, чтобы она удовлетворяла поставленным требованиям.

Для широкого круга управляемых механических систем, таких как станки с программным управлением, манипуляторы промышленных роботов и т.п., САУ образуется из трех регуляторов – положения, скорости и ускорения.

Таким образом, структура подчиненного регулирования в принципе обеспечивает возможность настройки каждого внутреннего контура независимо от настройки его внешних контуров. Благодаря этому в такой структуре возможно введение в контур регулирования параметра дополнительных формирующих и корректирующих устройств, необходимых для получения требуемого качества регулирования этой величины, так что эти устройства не оказывают влияния на качество работы всех контуров регулирования, внутренних по отношению к данному.

На практике широко применяются настройки регулятора на технический (модульный) оптимум и симметричный оптимум, обеспечивающие желаемые переходные процессы, что достигается оптимальным соотношением постоянных времени объектов и регуляторов. В этих случаях в каждом контуре САУ выделяется звено с большой постоянной времени 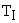(например, 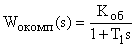, которая компенсируется постоянной времени регулятора 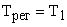, остальные звенья с малыми постоянными времени с достаточной для практических расчетов точностью заменяются одним апериодическим 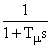, где суммарная малая постоянная времени определяется выражением

_.

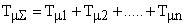Передаточная функция регулятора в этом случае представляется как:

,

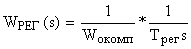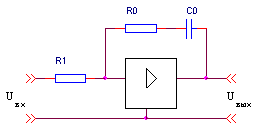
Интегрирующее устройство вводится для устранения влияния случайных возмущений на объект управления. Структурная схема такой системы приведена на рис. 4.

Передаточные функции разомкнутой и замкнутой системы на рис.4 можно представить в виде:

.

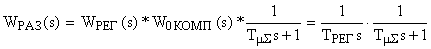
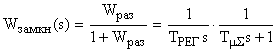Из последнего выражения видно, что переходные процессы в системе при отработке задающего воздействия не зависят ни от коэффициента усиления, ни от больших инерционностей объекта, которые скомпенсированы, а зависят только от некомпенсированных малых постоянных времени объекта регулирования 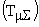и от постоянных времени регулятора .

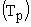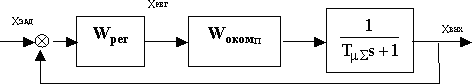
Рис. 4. Обобщенная структурная схема оптимизированного контура регулирования

При выборе 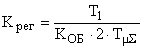; 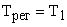считается, что настройка будет выполнена на модульный оптимум, которому соответствует перерегулирование 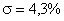, время переходного процесса 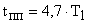. При такой настройке .

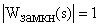Если выбрать 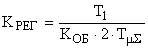; 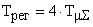, то считается, что настройка будет выполнена на симметричный оптимум, которому соответствует перерегулирование 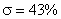, время переходного процесса 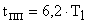_. При такой настройке логарифмическая амплитудно-частотная характеристика разомкнутой системы будет симметрична относительно частоты среза.

Выбор типа регулятора (П, ПИ, ПИД) в системе подчиненного регулирования и расчет его настройки (выбор оптимума, расчет параметров) осуществляется с помощью таблиц 1, 2 и 3. в зависимости от числа больших постоянных времени и типов звеньев в контурах, и соотношения больших и малых постоянных времени.

Таблица 1 Выбор типа регулятора и метода его настройки

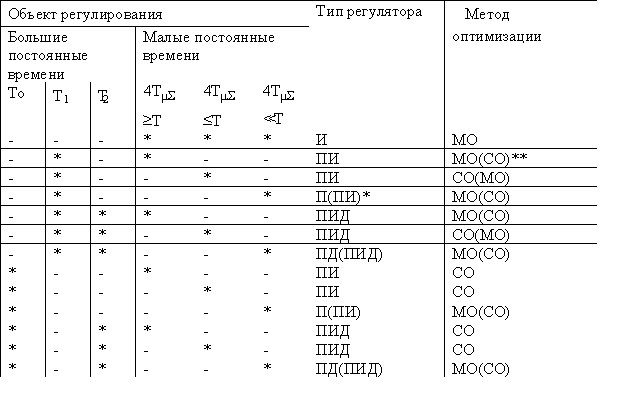
Примечание:

1. 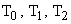– большие постоянные времени соответственно интегрирующего и апериодических звеньев в объекте.

2.* — указанные в скобках типы регуляторов применяют когда статическая ошибка с П-регулятором недопустимо велика.

3. ** — указанные в скобках методы оптимизации характеризуются более длительным временем, в течении которого устраняется отклонение регулируемой величины при возмущающих воздействиях (динамическая ошибка регулирования).

Таблица 2 Расчет параметров регуляторов

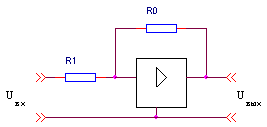
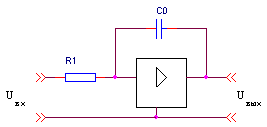
В качестве регуляторов применяют операционные усилители с входными цепями и цепями обратной связи. В зависимости от вида элементов этих цепей и способа их соединения операционные усилители могут выполнять операции сложения, вычитания, пропорционального усиления, интегрирования, дифференцирования, а также любую комбинацию этих операций. В табл.2.3 представлены схемы и передаточные функции регуляторов различного типа.

Таблица 3 Параметры конструктивных элементов регуляторов

Тип регулятора	Передаточная функция регулятора	Схема регулятора	Параметры регулятора
П-регулятор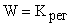
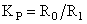
И-регулятор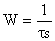
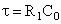
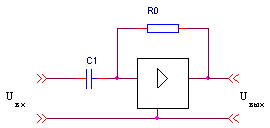
Д-регулятор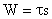
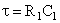
ПИ-регулятор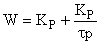

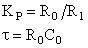
9.4. Модальное управление в САУ

Синтез систем управления на основе частотных методов позволяет при заданной структуре САУ выбрать ее параметры, обеспечивающие требуемое качество процесса регулирования. Такая задача реализуема, если число регулируемых параметров невелико – один или три. Однако с помощью этих методов нельзя придать корням замкнутой системы желаемое расположение, обеспечивающее необходимые ее динамические характеристики. Помещение этих корней в любые наперед заданные положения составляет предмет теории модального управления. Если вектор состояния объекта может быть измерен полностью, то обеспечение заданного расположения корней не вызывает трудностей. Это достигается в том случае, если матрица связи CY вектора измеряемых переменных YY(t) и вектора состояния управляемого объекта X(t) имеет размерность 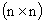, а ее ранг равен порядку системы дифференциальных уравнений, описывающих объект. При этом составляющими вектора измеряемых переменных могут быть не только измеряемые переменные состояния, но и измеряемые линейные комбинации этих переменных.

Если матрица CY имеет размерность 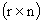(, где 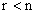, а ее ранг равен r, то управляемый объект относится к классу систем с неполной информацией о переменных состояния, так как в этом случае определить из уравнения 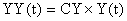по измеренному вектору все компоненты вектора состояния X(t) не представляется возможным.

При синтезе систем модального управления используется метод стандартных коэффициентов, при котором задается оптимальное распределение корней. Наиболее широко используется распределение корней, предложенное Баттервортом. Оно заключается в том, что корни характеристического уравнения распределяются в левой полуплоскости по окружности радиуса , величина которого определяет быстродействие системы. Стандартные формы Баттерворта характеризуются симметричным распределением коэффициентов характеристического полинома системы. Получаемые при использовании распределения Баттерворта характеристические полиномы приводят к некоторой колебательности переходных характеристик. Наилучшие результаты при использовании метода стандартных коэффициентов достигаются для систем, числитель передаточной функции которых не содержит нулей. Однако и при другом виде числителя эти формы могут быть полезны, так как могут служить отправной точкой при отыскании оптимального распределения корней.

При управлении положением корней в случае полной информации о переменных состояния рассматривается линейный стационарный объект, описываемый уравнением вида

.

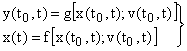Рассмотрим замкнутую систему, то есть добавим к уравнению объекта уравнение регулятора вида

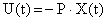
(1)

где Р – матрица обратных связей размерностью .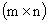

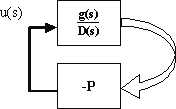
Рис. 5. Структурная схема САУ

Объединяя (1) и уравнение объекта, представленное в виде системы уравнений (2)

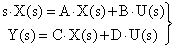
(2)

получим

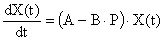
(3)

Матрица обратных связей выбирается таким образом, чтобы придать матрице 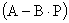заранее предписанное расположение собственных значений, то есть корней характеристического уравнения матричного уравнения (3). В том случае, когда машинный агрегат имеет один входной сигнал, вместо вектора 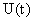будет фигурировать скалярная величина U, а вместо матрицы 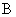размерностью 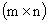– матрица-столбец b. В таком случае прямоугольная матрица Р переходит в матрицу-строку р, содержащую n элементов. Структурная схема такой системы представлена на рис. 3. Характеристическое уравнение такой системы имеет вид

.

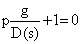Приводя левую часть этого выражения к общему знаменателю, обозначив получившийся числитель через 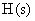, получаем соотношение

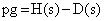
(4)

где 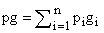— скалярное произведение матрицы-столбца числителя передаточной функции и транспонированной матрицы-столбца 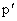, характеризующей свойства цепи обратной связи, 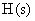– стандартная форма характеристического полинома для заданной размерности объекта управления.

Соотношение (4) позволяет достаточно просто находить структуру и параметры регулятора, обеспечивающего желаемое распределение корней замкнутой системы.

При неполной информации об управляемом объекте обратная связь формируется на базе матричного уравнения

,

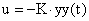где К – матрица-строка, содержащая r элементов.

Задача управления движением управляемого объекта решается аналогично рассмотренному выше случаю. Однако в последнем случае возможно управление распределением корней характеристического полинома системы лишь в определенных пределах. Чтобы получить большую свободу управления корнями в прикладных задачах, увеличивают число чувствительных элементов, устанавливаемых на объекте, то есть формируют выходной вектор, дающий более полную информацию о переменных состояния управляемой системы.

Вопросы.

1. Что понимается под проектированием САУ?

2. Какие существуют методы синтеза САУ по заданным динамическим характеристикам?

3. В чем заключается суть коррекции динамических свойств САУ с помощью последовательного корректирующего устройства?

4. Как определяются параметры желаемой частотной характеристики системы автоматического управления?

5. Как определяются параметры последовательного корректирующего устройства?

6. Какие принципы используются при построении систем подчиненного управления?

7. Что называется модульным оптимумом?

8. Что называется симметричным оптимумом?

9. Чем отличаются системы подчиненного управления от САУ с последовательной коррекцией?

10. Какие принципы используются при построении САУ на базе модального управления?

11. Какова структура САУ, в которой используются принципы модального управления?

12. Как определяются параметры обратных связей в САУ с модальным управлением?

13. Чем отличаются принципы модального и подчиненного управления САУ?

Тема 10. Наблюдающие устройства.

Развитие идеи вычисления ряда переменных состояния объекта на базе относительно небольшого числа измеряемых переменных состояния позволяет с использованием известных в автоматическом управлении приемов, таких как введение обратных связей, элементов адаптации или самонастройки, позволяет создавать наблюдающие устройства для управляемых объектов с низкой чувствительностью к вариации их параметров. В настоящее время известны два таких подхода косвенного определения компонент вектора состояния управляемого объекта, недоступных прямому измерению. Они связаны с применением наблюдающих устройств, предложенных Калманом (фильтр Калмана) и Льюинбергером.

При использовании фильтров Калмана детерминированный подход к рассмотрению анализируемой системы автоматического управления заменяется стохастическим.

Областью применения таких наблюдающих устройств являются в основном системы управления сложными электромеханическими устройствами. При анализе детерминированных механических систем задача оценки всех переменных состояния управляемого объекта может быть решена с помощью более простого устройства, называемого наблюдающим устройством Льюинбергера. Входными сигналами для этого устройства служат доступные измерению выходные координаты объекта, а также поступающие на него входные воздействия.

10.1. Наблюдающие устройства Льюинбергера

Наблюдающие устройства Льюинбергера представляют собой динамическую систему, характеристики которой в известной степени могут выбираться произвольно. При этом вектор состояния этого устройства линейно связан с вектором состояния наблюдаемого устройства и, следовательно, может использоваться в качестве оценки последнего.

Рис. 1. Простое наблюдающее устройство

Обратимся к некоторым вопросам общей теории наблюдающих устройств. Для этого рассмотрим задачу наблюдения некоторого свободного объекта S, то есть системы, входные сигналы которой равны нулю. Если имеющиеся в распоряжении выходы этого объекта используются в качестве входов некоторой системы 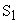, то последняя почти всегда может использоваться в качестве наблюдающего устройства рассматриваемого механизма в том смысле, что е¨ состояние отслеживает линейное преобразование исследуемого объекта (рис. 1).

Математически это выражается следующим образом. Для свободного объекта S, описываемого системой вида

,

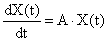воздействующего на наблюдающее устройство, представленное системой дифференциальных уравнений вида:

,

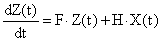существует некоторая матрица преобразования, которая должна удовлетворять условию вида 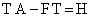. Тогда при нулевых начальных условиях имеет место линейное соответствие 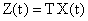, которое справедливо для всех 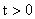. В более общем случае, когда 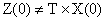, имеет место выражение

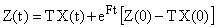
(1)

При отрицательности собственных значений матрицы F свободные колебания наблюдающего устройства, выражаемые вторым слагаемым выражения (1), затухают и вектор состояния 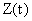данного устройства сводится к вектору .

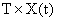Если на механизм воздействуют внешние силы, то происходящие в нем процессы описываются системой вида:

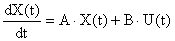
Тогда уравнение наблюдающего устройства принимает вид

.

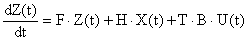Эта система также имеет решение вида (1). Отсюда следует, что наблюдающее устройство для возмущенного объекта можно синтезировать, первоначально полагая наблюдаемое устройство свободным, а затем добавляя к нему необходимые входные воздействия.

10.2. Наблюдающее устройство идентификации

Наблюдающее устройство идентификации характеризуется тем, что матрица преобразования Т, связывающая векторы состояния наблюдающего и наблюдаемого устройств, является единичной матрицей, то есть в установившемся режиме имеет место равенство 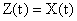. С учетом этого равенства .

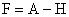Отсюда следует, что устройство идентификации имеет тот же порядок, что и наблюдаемый объект. Свойства наблюдающего устройства зависят от вида матрицы Н. Вид этой матрицы определяется как порядком измеряемого вектора 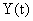выходных сигналов, так и структурой наблюдающего устройства. Если объект с r-мерным вектором выходных сигналов описывается уравнениями вида

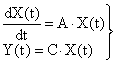
(2)

а устройство идентификации – уравнением

,

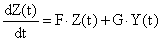то имеет место соотношение .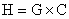

При синтезе устройства идентификации матрица С фиксирована и определяется свойствами объекта и используемой измерительной системы. Матрица G может изменяться произвольным образом, и свойства наблюдающего устройства однозначно определяются е¨ выбором. С учетом этого устройство идентификации описывается уравнением

.

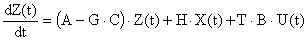Полная наблюдаемость системы (2) означает возможность определения начального состояния наблюдаемого объекта по его выходному сигналу, известному на некотором конечном интервале. Признаком полной управляемости является, как известно, равенство ранга матрицы наблюдаемости системы (2) ее порядку. Если наблюдаемый механизм или система управления его работой удовлетворяют этому условию, то корни наблюдающего устройства можно поместить в любые желаемые положения, то есть придать ему необходимые динамические показатели. Структура такого наблюдающего устройства представлена на рис. 2.

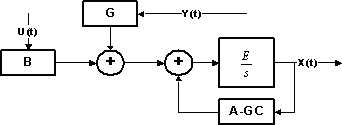
Рис. 2. Структурная схема устройства идентификации

Такое наблюдающее устройство обладает некоторой избыточностью. Это выражается в том, что с его помощью оценивается весь вектор состояния объекта. В то же время часть компонент этого вектора можно определить по результатам непосредственного их измерения на управляемом объекте. Эту избыточность можно устранить путем синтеза редуцированного наблюдающего устройства. Редуцированным наблюдающим устройством называется устройство, порядок характеристического уравнения которого меньше порядка характеристического полинома наблюдаемой системы.

10.3. Редуцированное устройство идентификации.

Для 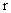— мерного вектора выходных сигналов 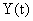достаточно синтезировать устройство идентификации размерности 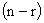, характеризуемое вектором состояния такой же размерности. Пусть исследуемый объект управления или механизм представляются системой дифференциальных уравнений вида

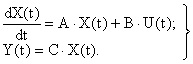
(3)

При этом r выходов объекта линейно независимы, что эквивалентно тому, что ранг матрицы 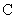равен r. Тогда оценку всего вектора 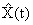можно получить из уравнения

.

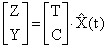Из этого уравнения вытекает выражение для определения оценки вектора состояния исследуемой системы, которая имеет вид

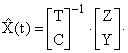
Вектор состояния исследуемой системы можно представить как

,

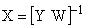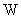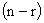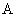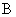где – вектор неизмеряемых переменных состояния исследуемой системы размерностью . Разбивая матрицы и системы уравнений (3) получаем систему уравнений

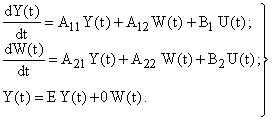
Из этих уравнений получается уравнение наблюдающего устройства идентификации, которое принимает вид

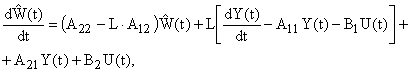
(4)

где 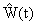— вектор выхода наблюдающего устройства размерностью 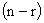, – матрица, определяющая расположение корней характеристического полинома наблюдающего устройства.