Замкнутой САУ называют систему, в которой процесс управления ОУ зависит от результата управления. 9 страница

.

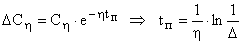Задание определенной степени быстродействия также ограничивает допустимую область расположения корней характеристического полинома, как это показано на рис. 5.

Степень быстродействия 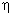можно найти используя постановку 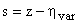, что соответствует смещению корней на величину 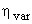. Далее, используя любой критерий устойчивости, подбирают значение 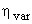, при котором система будет на границе устойчивости. И тогда: .

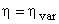Для рассмотрения обобщенных характеристик САУ используется понятие о среднегеометрическом корне 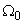. Пусть имеем характеристическое уравнение:

.

Приведем его к нормированному виду (разделим на 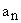и выполним подстановку ):

,

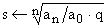где: 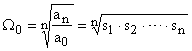- среднегеометрический корень.

Для статических САУ 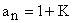, для астатических 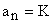, 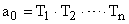. Следовательно, увеличивая 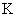, можно увеличить . На основании теоремы подобия увеличение вызовет пропорциональное радиальное смещение корней. Т.е. вид переходного процесса меняться не будет, но будет меняться его временной масштаб. Поэтому среднегеометрический корень 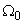является мерой быстродействия.

Для приведенного уравнения время будет безразмерным , переходная функция 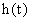в случае кратных вещественных корней или одной пары комплексных будет ограничена минорантой и мажорантой:

,

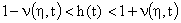где: — разложение в ряд Тейлора огибающей той составляющей в переходном процессе, корень которой ближе к оси " ".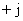

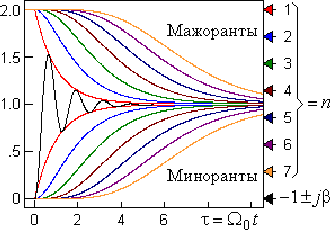
Рис. 6. Распределение корней и вид переходной функции

На рис. 6 демонстрируется, что любой переходный процесс в любой системе будет затухать тем медленней, чем больше корней вблизи оси "+1".

8.4. Интегральные оценки качества

Интегральные оценки дают обобщенную оценку быстроты затухания и величины отклонения регулируемой величины, в виде единого числового значения.

Находят применение первые три из перечисленных в списке интегральные оценки:

и — линейные интегральные оценки (не чувствительны к высшим производным координат САУ).

и — квадратичные интегральные оценки (не чувствительны к высшим производным координат САУ).

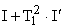— улучшенная квадратичная интегральная оценка (чувствительна к значению скоростной составляющей в движении координат САУ).

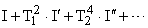— интегральные оценки более высоких порядков (чувствительны к значению скорости, ускорению,... координат САУ).

Графическая интерпретация свойств линейной и квадратичной интегральных оценок представлена на рис. 7.

1. Пусть имеем переходные функции .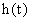

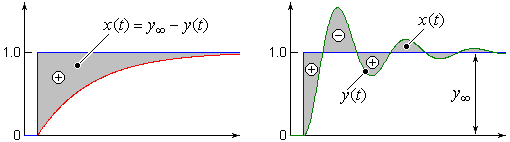
Рис. 7. Линейная и интегральная квадратичные оценки качества САУ

Рассмотрим линейные интегральные оценки:

и .

Очевидно, что чем меньше значение оценки или , тем лучше переходный процесс, но:

a) Оценка не может применяться к колебательному переходному процессу.

b) Аналитическое вычисление оценки по коэффициентам уравнения ошибки затруднено.

c) Одно значение оценки может соответствовать переходным процессам с разной колебательностью (если совпадают мажоранты и миноранты).

2. Ограничения "a" и "b" для оценок и преодолеваются квадратичными интегральными оценками 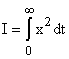и :

и ..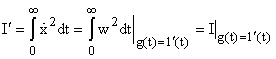

Заметим, что оценку можно получить нахождением оценки , если подать на вход САУ не ступенчатую 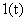, а дельта функцию 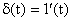. Применение оценки ограничено тем, что она не чувствительна к установившемуся значению ошибки .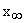

3. Ограничение "b" для оценок , , и снимается улучшенной квадратичной интегральной оценкой:

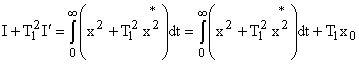
где: 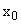— начальное значение отклонения в переходном процессе.

Очевидно, что 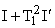будет минимальна при 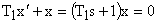. Решение этого дифференциального уравнения есть экспонент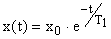а: , а .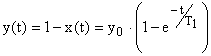

Следовательно, улучшенная квадратичная интегральная оценка 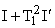будет иметь минимум при приближении переходной функции к заданной экспоненте (с постоянной времени ).

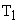4. Можно использовать улучшенные интегральные оценки более высоких порядков. Например:

.

Здесь оценка будет иметь минимум, только при перемещениях координат САУ с определенными скоростью и ускорением, которые определены постоянными времен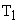и и соответственно. Очевидно, что дифференциальным уравнением второго порядка можно определить желаемый переходный процесс с заданным затуханием.

Определение величин интегральных оценок может производиться аналитическими и численными методами. Последние заключаются в интегрировании величины ошибки САУ в процессе определения ее переходных характеристик. Аналитический расчет квадратичных интегральных оценок позволяет вычислять их величины непосредственно по передаточным функциям САУ.

Для аналитического расчета можно воспользоваться теоремой Парсеваля:

.

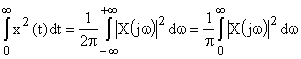Если ошибка 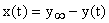, то ее изображение:

.

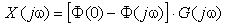Для нахождения и мы должны подавать сигналы 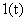и 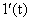. Их изображения Фурье соответственно равны:

и .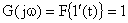

Тогда установившиеся значения выходной координаты и, соответственно, значения передаточная функция для этих режимов:

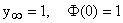и .

В итоге изображения ошибок:

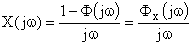и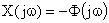

А квадратичные интегральные оценки определяются как:

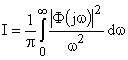и .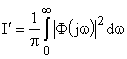

8.5. Частотные критерии качества

Частотные критерии качества применяют, когда известны или можно определить экспериментально частотные свойства САУ (АФХ, АЧХ, ЛАЧХ & ЛФЧХ). Вид переходного процесса при этом не рассматривается.

Оценить частотными критериями можно:

Запас устойчивости ( )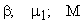

Быстродействие САУ ( ).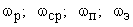

При использовании амплитудно-частотной характеристики замкнутой САУ (рис. 8) возможно определение:

· запаса устойчивости по фазе ,

· полосы пропускания – частоты, при которой модуль АЧХ равен 0.707 от ее значения при нулевой частоте.

· показатель колебательности, который является удобным критерием запаса устойчивости и определяется как:

.

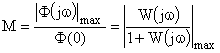Показатель колебательности М равен максимальному значению приведенной к коэффициенту усиления в области низких частот АЧХ замкнутой системы. Т.е. вынужденное движение на резонансной частоте будет иметь амплитуду в M раз большую, чем в области низких частот. И чем больше M, тем меньше запас устойчивости.

Рис. 8. Связь качественных показателей САУ и частотной характеристики замкнутой САУ

По вещественной частотной характеристике замкнутой САУ можно определить:

— величину перерегулирования по максимальному значению ВЧХ 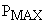и ее значению при 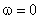– 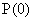, как

.

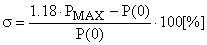Если 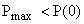, то величина перерегулирования всегда меньше 18%;

— быстродействие САУ по интервалу положительности вещественной частотной характеристики как

.

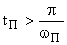По виду АФХ разомкнутой системы (рис. 9) оценивают величины запас устойчивости:

по амплитуде — и .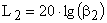

по фазе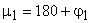

где: 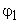— запаздывание по фазе на частоте единичного усиления при 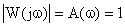или (по ЛАЧХ).

Рис. 9. Связь качественных показателей САУ и ее АФЧХ

Для абсолютно устойчивых систем имеет смысл только величина , т.к. 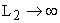. Для хорошо демпфированных систем передаточная функция имеет 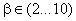т.е. (6...20) дБ.

Запас устойчивости тем больше, чем больше и . Используя и можно задать запретную область для АФХ. Но недостаток заключен в том, что если АФХ будет касаться запретной области в разных точках, перерегулирование будет разным.

Если имеется только АФХ разомкнутой системы , то показатель колебательности M удобно использовать в виде нанесенной сетки, представляющей линии уровня 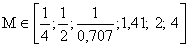, как это показано на рис. 10, где: (1) — уравнение окружности с радиусом R, и центром в точке C.

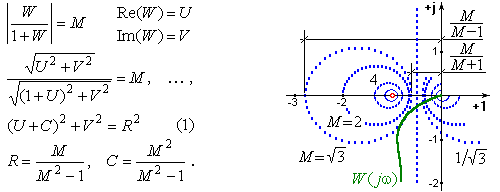
Рис. 10. Определение показателя колебательности по АФЧХ.

Оценить быстродействие САУ можно по частотным характеристикам замкнутой и разомкнутой системы. При этом используется:

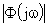— амплитудную замкнутой системы;

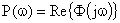- вещественную частотную характеристику;

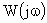— амплитудно-фазовую частотную разомкнутой системы;

При оценке быстродействия САУ по виду логарифмических частотных характеристик в качестве критериев используют следующие величины:

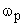- резонансная частота, соответствует пику АЧХ, близка к частоте колебаний в переходном процессе;

- частота среза, соответствующая условию 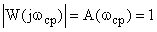или (по ЛАЧХ).

- частота соответствующая полосе пропускания замкнутой системы 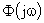, определяемая из условия .

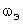- эквивалентная полоса пропускания замкнутой системы: 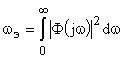, — эта величина связана с порогом пропускания системой помех. Кроме того, если ее рассчитать, включая отрицательные частоты, причем в герцах, то она совпадет с квадратичной интегральной оценкой .

Вопросы.

1. Какие показатели характеризуют динамические режимы работы САУ?

2. Что называется быстродействием САУ?

3. Какие тестовые сигналы используются для сравнения качественных показателей работы САУ в динамических режимах?

4. Что называется перерегулированием в переходном процессе?

5. Что называется интегральной оценкой качества переходных процессов в САУ? Какие существуют виды интегральных квадратичных оценок?

6. Что называется линейной интегральной оценкой качества?

7. Что называется запасом устойчивости по амплитуде и фазе САУ?

8. Как влияет величина устойчивости по фазе на величину перерегулирования?

9. Какие виды частотных характеристик и каким образом они используются для определения качественных показателей работы САУ в динамических режимах?

10. Как влияет распределение корней характеристического полинома на динамические характеристики САУ?

11. Как определить допустимую область распределения корней по требованиям к качественным показателям работы САУ в динамических режимах?

12. Как определяются интегральные показатели работы САУ?

13. Возможно ли использование линейных интегральных оценок для САУ с колебательными переходными характеристиками?

Тема 9. Проектирование регуляторов технологических агрегатов

9.1. Общие замечания

Под проектированием регуляторов САУ, а в частности электроприводов электромеханических систем, понимают инженерную задачу, заключающуюся в выборе типа и параметров корректирующих устройств, обеспечивающих требуемые динамические свойства проектируемого привода. Методологический подход к решению проблемы синтеза большинства электроприводов заключается в разделении проектирования на ряд этапов, основными из которых являются:

· обоснование рациональной структуры электропривода и типа корректирующих устройств, обеспечивающих необходимые запас устойчивости и качество переходных процессов при линеаризованной непрерывной части системы;

· параметрический синтез корректирующих устройств при линеаризованных характеристиках основных элементов системы;

· выбор и расчет специальных корректирующих устройств, предназначенных для обеспечения заданной точности или близких к оптимальным режимов работы электропривода.

Наиболее ответственным и наименее подверженным машинным методам проектирования является первый этап этих работ, а именно выбор типа корректирующих устройств и способов их включения. Поэтому на этом этапе существенную роль играют опыт, профессиональная подготовка и интуиция инженера-проектировщика.

Универсальным методом параметрического синтеза корректирующих устройств, проводимых с учетом основных особенностей электропривода, является его моделирование. Однако этот метод не может быть эффективно использован без предварительного аналитического исследования проектируемого объекта, предназначенного для обоснования выбранной структуры электропривода, определения его качественных показателей и предварительного выбора параметров корректирующих устройств. При этом аналитические методы позволяют исследовать вопрос в общем виде и среди множества возможных решений проблемы синтеза САУ найти близкое к оптимальному.

В современной научно-технической литературе, посвященной вопросам теории САУ, можно проследить несколько подходов к определению структуры и параметров корректирующих устройств. Первый заключается в определении желаемых частотных характеристик системы и преобразовании исходных частотных характеристик к желаемому виду. Этот метод называется методом логарифмических частотных характеристик. Сутью второго метода является компенсация инерционных свойств управляемого объекта с использованием вложенных друг в друга контуров управления отдельными составляющими вектора состояния объекта. Реализация такого подхода к выбору корректирующих устройств осуществляется в рамках методов подчиненного управления. Последний метод заключается в формировании заданного распределения корней характеристического полинома системы посредством введения обратных связей по отдельным составляющим вектора состояния управляемого объекта. Этот метод используется при построении систем модального управления.

9.2. Синтез САУ методом логарифмических частотных характеристик

Метод логарифмических частотных характеристик используется для определения частотных передаточных функций корректирующих устройств, приближающих динамические показатели к желаемым. Наиболее эффективно этот метод применяется для синтеза систем с линейными или цифровыми корректирующими устройствами, поскольку в таких системах частотные характеристики звеньев не зависят от амплитуды входных сигналов. Синтез САУ методом логарифмических частотных характеристик включает в себя следующие операции.

На первом этапе по известной передаточной функции неизменяемой части САУ строится ее логарифмическая частотная характеристика 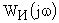. В большинстве случаев достаточно использование асимптотических частотных характеристик.

На втором этапе строится желаемая логарифмическая частотная характеристика САУ 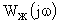, которая удовлетворяла бы поставленным требованиям. Определение вида желаемой ЛАЧХ проводится исходя из назначения системы, времени переходного процесса, перерегулирования и коэффициентов ошибок. При этом часто используются типовые частотные характеристики для систем с разным порядком астатизма. При построении желаемой ЛАЧХ необходимо быть уверенным, что вид амплитудной характеристики полностью определяет характер переходных процессов и нет необходимости вводить в рассмотрение фазовую частотную характеристику. Последнее справедливо в случае минимально-фазовых систем, для которых характерно отсутствие нулей и полюсов, расположенных в правой полуплоскости. При выборе желаемых логарифмических амплитудной и фазовой характеристик важно, чтобы последняя обеспечила требуемый запас устойчивости при частоте среза системы. Для этого используют специальные номограммы, вид которых приводится на рис. 1.

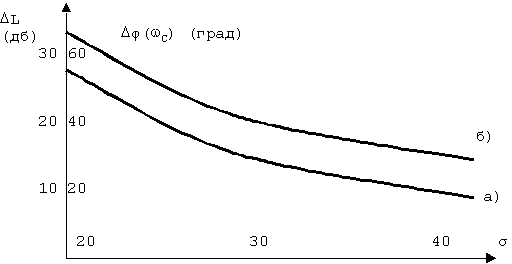
Рис. 1. Кривые для выбора запаса устойчивости по амплитуде (а)и фазе (б) в зависимости от величины перерегулирования.

Удовлетворительные качественные показатели САУ в динамических режимах достигаются при пересечении амплитудной характеристики оси абсцисс с наклоном –20 дб/дек.

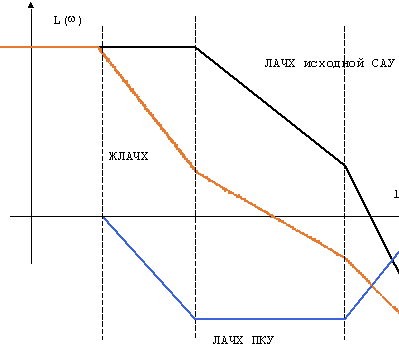
Рис. 2. Определение характеристик ПКУ

На последнем этапе из сравнения частотных характеристик некорректированной системы и желаемых частотных характеристик определяются частотные свойства корректирующего устройства. При использовании линейных средств коррекции логарифмическая частотная характеристика последовательного корректирующего устройства (ПКУ) 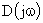может быть найдена вычитанием ЛАЧХ некорректированной системы из желаемой ЛАЧХ САУ, то есть

.

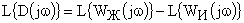Следовательно

.

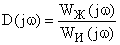Следует отметить, что по передаточной функции последовательного корректирующего устройства 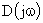легко определить передаточные функции звеньев в цепи прямой или обратной связи, с помощью которых осуществляется коррекция динамических показателей САУ.

Следующим этапом является определение способа реализации, схемы и параметров корректирующего устройства.

Последним этапом синтеза устройства коррекции является проверочный расчет САУ, который заключается в построении графиков переходных процессов для системы с выбранным корректирующим устройством. На этом этапе целесообразно использование средств вычислительной техники и моделирующих программных комплексов VinSim, WorkBench, CircuitMaker, MathCAD.

9.3. Подчиненное управление в САУ

Назначение регуляторов электроприводов состоит в том, чтобы путем обеспечения выполнения требований к исполнительной электромеханической системе по точности, устойчивости и качеству переходных процессов достигнуть цели управления. Обстоятельствами, усложняющими выбор структуры и параметров регуляторов приводов электромеханических систем, являются наличие внешних и внутренних силовых воздействий и позиционных силовых связей, погрешности преобразователей информации, используемых для создания корректирующих обратных связей. Эффективным путем повышения динамической точности приводов электромеханических систем является увеличение коэффициентов усиления сигналов рассогласования при одновременном введении корректирующих связей, способствующих возрастанию запасов устойчивости, применение пропорционально — интегрирующих (ПИ) регуляторов и построение комбинированных систем с искусственными компенсирующими связями по задающим и возмущающим воздействиям. Введение комбинированного управления по производным от задающих воздействий – это основное направление снижения ошибок воспроизведения запрограммированных траекторий движения исполнительных систем технологического оборудования.

Исходные требования к электромеханической системе могут быть трансформированы в требования к электроприводу и представлены в виде желаемой ЛАЧХ по цепи преобразования задающего воздействия в регулируемую переменную (обобщенную координату механизма) или в виде требуемого распределения корней. Для повышения стабильности динамических свойств электроприводов исполнительной системы применяются корректирующие обратные связи, элементы которых должны иметь постоянные параметры.

Одним из способов реализации средств коррекции электромеханических систем является использование принципа построения подчиненных контуров регулирования. В этом случае регулятор электропривода образуется из нескольких вложенных друг в друга контуров управления. Преимущество такого подхода состоит в том, что контуры регулирования можно настраивать по очереди: сначала внутренний, затем – внешний. Настроенный внутренний контур выступает в роли объекта управления для регулятора внешнего контура. Примерная схема многоконтурного электропривода показана на рис. 3. В основу построения подобных систем положены следующие принципы: