Пример расчета (задача № 1)

Для стального бруса квадратного сечения сжатого силой Р с учетом собственного веса при исходных данных приведенных ниже, требу­ется (рис. 2.3, а):

1. Определить количество расчетных участков;

2. Составить аналитические выражения для нормальных сил N_z , нормальных напряжений s_z и вычислить их значения для каж­дого из участков с учетом их собственных весов;

3. Построить эпюры N_z и s_z ;

4. Вычислить перемещение верхнего конца колонны от дейст­вия силы Р и собственного веса.

Исходные данные: Р = 20 кН; l₁ = l₂ = l₃ = 0,4 м; модуль упругости стали Е = 2,1×10⁸ кН/м²; F₁ = 4×10^{-2 м2}; F₂ = 9×10^{-2 м2}; F₃ = 25×10^{-2 м2}; g = 78 кН/м³ .

Решение

1. Определение количества участков. Так как нор­мальная сила N_z зависит от величин внешних сил, в данном случае включающих в себя и собственный вес колонны, а последний, в свою очередь, от размеров попе­речного сечения F_i и объемного веса g, то границами участков следует назначать те сечения, в которых приложены внешние сосредоточенные силы и где происходит скачкообразное изменение площади попе­речного сечения или объемного веса материалов конструкций.

Исходя из вышесказанного, учитывая g = const, брус будет иметь три участка:

1 участок - от 0 до сечения В (где приложена сила Р);

2 участок - от сечения В до сечения С;

3 участок - от сечения С до сечения D.

Следует заметить, что при определении нормальных напряже­ний используются те же участки.

2. Составить аналитические выражения для нор­мальных сил N_z, нормальных напряжений s_z и вычис­лить их значения для каждого из участков, с учетом их собственных весов. Для этого воспользуемся методом сече­ний.

1 участок (0 - В) 0 £ z₁ £ 0,4 м.

Проведя сечение 1 - 1 на расстоянии z₁ от начала координат (точка 0), рассмотрим равновесие верхней части. При этом, к рас­сматриваемой части прикладываются в центре ее тяжести собствен­ный вес и нормальная сила 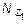, заменяющую действие отброшен­ной нижней части бруса на верхнюю рассматриваемую (рис. 2.3, б). Составив уравнение равновесия рассматриваемой верхней части ко­лонны по оси z , получим:

.

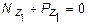В свою очередь, собственный вес верхней части колонны оп­ределяется следующим образом:

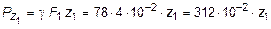кН.

Тогда выражение для нормальной силы будет иметь вид:

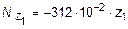кН,

а для нормальных напряжений :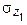

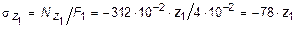кН/м².

Так как, 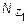и 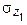линейно зависят от z₁ , то для построения их графиков (эпюр) достаточно определить значения этих величин на границах участка, т.е.

при z₁ = 0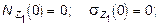

при z₁ = 0,4 м 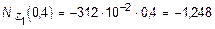кН;

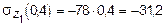кН/м².

Знаки минус пр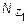и и 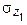указывают на то, что принятое на­правление для этих величин не совпадает с действительным, т. к. в принятой схеме продольная сила не растягивает, а сжимает первый участок.

2 участок (В - С) 0,4 м £ z₂ £ 0,8 м.

Аналогично предыдущему проводим сечение 2-2 на расстоянии z₂ (рис. 2.3, в). Для верхней части составляем уравнение равновесия åz = 0 .

В это уравнение войдут: собственный вес первого участка Р₁ = = g F₁ l₁; собственный вес отсеченной части второго участка 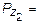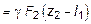; сосредоточенная сила Р = 20 кН, а также сила .

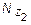Тогда уравнение равновесия примет вид:

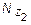Р₁ + + P + = 0,

отсюда

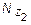= -P - g F₁l₁ - = -20 - 78×4×10^-2×0,4 - 78×9×10^-2 (z₂ -0,4) =
= -7,02×(z₂ + 2,62678) кН.

Учитывая постоянство площади поперечного сечения на втором участке, выражение для нормального напряжения может быть запи­сано таким образом:

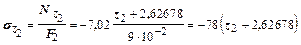êÍ/ì².

Вычислим значения ординат 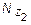и 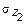в граничных сечениях второго участка:

при z₂ = 0,4 м 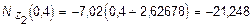кН,

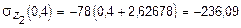кН/м²;

при z₂ = 0,8 м 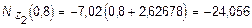кН,

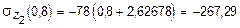кН/м².

3 участок (С - D) 0,8 м £ z₃ £ 1,2 м.

Составив уравнение равновесия åz = 0 (рис. 2.3, г) для верхней части бруса, получим:

Р₁ + Р₂ + 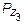+ P + = 0,

откуда

= -P - g F₁l₁ - g F₂l₂ - g F₃(z₃ - l₁ - l₂) = -20 - 78×4×10^-2×0,4 -
- 78×9×10^-2 ×0,4 - 78×25×10^-2 (z₃ - 0,8) = -19,5×(z₃ + 0,43364) кН.

Выражение для напряжения:

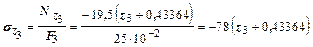кН/м².

Вычислим значения ординат и в граничных сечениях третьего участка:

при z₃ = 0,8 м (0,8) = -19,5 (0,8 + 0,43364) = -24,056 кН,

(0,8) = -78 (0,8 + 0,43364) = -96,224кН/м²;

при z₃ = 1,2 м (1,2) = -19,5 (1,2 + 0,43364) = -31,856 кН,

кН/м².

3. Построение эпюр N_z и s_z По причине линейной зависимости нормальной силы и напряжений от координаты z для построения их эпюр достаточно значений N_z иs_z в граничных сечениях каждого из участков (см. рис. 2.3, д, е). Необходимым условием правильности построения этих графиков является выпол­нение следующих требований:

- скачок в эпюре N_z должен находиться в точке приложения сосредоточенного усилия и быть равным по величине значению этой силы;

- скачки в эпюре s_z должны совпадать с точками приложения внешней силы Р и изменения площади поперечного сечения ко­лонны.

После анализа полученных эпюр (рис. 2.3, д, е) легко можно убедиться, что построения выполнены правильно.

4. Вычисление перемещения верхнего конца ко­лонны от действия всех сил. Полное перемещение со­гласно закону Гука может быть вычислено по формуле

.

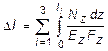В данном случае это выражение принимает следующий вид:

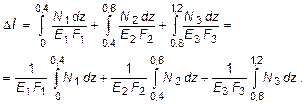
Так как величины определенных интегралов равны площадям, очерченным соответствующими подынтегральными функциями, то для вычисления перемещений Dl_i достаточно вычислить площади эпюры N_z на каждом из этих участков и разделить их на E_i F_i . Следовательно,

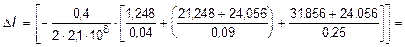
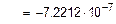м.