Перемещения и деформации

Под действием внешних сил твердые тела изменяют свою гео­метрическую форму, а точки тела неодинаково перемещаются в пространстве. Вектор 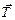, имеющий свое начало в точке А недефор­мированного состояния, а конец в т. 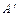деформированного состоя­ния, называется вектором полного перемещения т. А (рис. 1.5, а). Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, v и w, соответственно.

Для того, чтобы охарактеризовать интенсивность изменения формы и размеров тела, рассмотрим точки А и В его недеформиро­ванного состояния, расположенные на расстоянии S друг от друга (рис. 1.5, б).

Рис. 1.5

Пусть в результате изменения формы тела эти точки перемес­тились в положение А¢ и В¢, соответственно, а расстояние между ними увеличилось на величину DS и составило S + DS. Величина

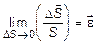(1.6)

называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей xyz, то в обозначения соответствующих проекций линейной деформации вводятся индексы e_x , e_y , e_z .

Линейные деформации e_x , e_y , e_z характеризуют изменения объема тела в процессе деформирования, а формоизменения тела - угловыми деформациями. Для их определения рассмотрим прямой угол, образованный в недеформированном состоянии двумя отрез­ками ОD и ОС (рис. 1.5, б). При действии внешних сил указанный угол DOC изменится и примет новое значение D¢O¢C¢. Величина

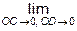(Ð DOC - Ð D¢O¢C¢) = g (1.7)

называется угловой деформацией, или сдвигом в точке О в плос­кости СОD. Относительно координатных осей деформации сдвига обозначаются g_xy , g_xz , g_yz .

Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в данной точке образует деформиро­ванное состояние в точке.

1.6. Закон Гука и принцип независимости
действия сил

Многочисленные экспериментальные наблюдения за поведени­ем деформируемых тел показывают, что в определенных диапазо­нах перемещения точек тела пропорциональны действующим на него нагрузкам. Впервые указанная закономерность была высказана в 1776 году английским ученым Гуком и носит название закона Гука.

В соответствии с этим законом перемещение произвольно взя­той точки А (рис. 1.5, а) нагруженного тела по некоторому направ­лению, например, по оси x, а может быть выражено следующим образом:

u = d_x P, (1.8)

где Р - сила, под действием которой происходит перемещение u; d_x×- коэффициент пропорциональности между силой и перемеще­нием.

Очевидно, что коэффициент d_x зависит от физико-механиче­ских свойств материала, взаимного расположения точки А и точки приложения и направления силы Р, а также от геометрических особенностей си­стемы. Таким образом, последнее выражение следует рассматривать как закон Гука для данной системы.

В современной трактовке закон Гука определяет линейную за­висимость между напряжениями и деформациями, а не между си­лой и перемещением. Коэффициенты пропорциональности в этом случае представляют собой физико-механические характеристики материала и уже не связаны с геометрическими особенностями си­-

стемы в целом.

Системы, для которых соблюдается условие пропорционально­сти между перемещениями и внешними силами, подчиняются принципу суперпозиции, или принципу независимости действия сил.

В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил. То есть, если к системе прило­жено несколько сил, то можно определить внутренние силы, на­пряжения, перемещения и деформации от каждой силы в отдель­ности, а затем результат действия всех сил получить как сумму действий каждой силы в отдельности. Принцип независимости действия сил является одним из основных способов при решении большинства задач механики линейных систем.