Возможные перемещения.

Обобщенные координаты 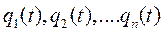представляют функции вре­мени, определяемые интегрированием при заданных начальных усло­виях дифференциальных уравнений движения, выражающих законы механики. Этой совокупностью функций времени 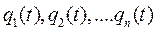определяется истинное движение системы. Дифференциалы 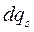обоб­щенных координат представляют их бесконечно малые изменения в истинном движении, пропорциональные промежутку времени dt : .

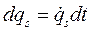При формулировании общих положений механики оказывается полезным ввести в рассмотрение бесконечно малые величины иной при­роды. Отвлекаясь от движения, зададимся вопросом, какое множество конфигураций в этот момент времени допускают связи системы. Если ограничиться рассмотрением конфигураций бесконечно близких к истинным и через 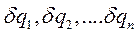обозначить бесконечно малые приращения обобщенных координат, называемые их вариациями, то упомянутое множество определится совокупностью величин

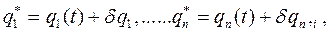
где в случае голономной системы вариации 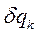совершенно произ­вольны. Мы можем сказать, что в момент t связи такой системы, имеющей n степеней свободы, допускают 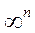конфигураций.

Рассмотрим точку системы 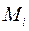, задаваемую вектор-радиусом 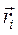. Изменение 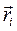за промежуток времени dt определяется дифферен­циалом

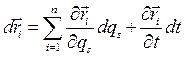(4.2)

представляющим бесконечно малое перемещение точки 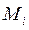в истин­ном движении системы. Ему противопоставляется виртуальное или возможное перемещение точки 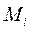, обозначаемое 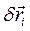. Этот беско­нечно малый вектор представляет изменение вектор-радиуса точки при мысленном переведении системы из рассматриваемой конфигура­ции в одну из ( 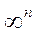) допускаемых связями бесконечно близких конфигураций; он вычисляется в фиксированный момент t с точностью до первых степеней относи­тельно вариаций :

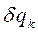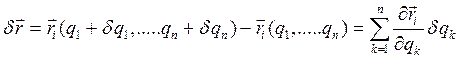(4.3)

Если связи не зависят от времени, то в выражении (4.2) отпадает последнее слагаемое. Дифференциалы 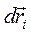связаны теми же соотношениями, что и ва­риации 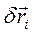; и истинное перемещение

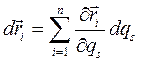
принадлежит множеству виртуальных или возможных перемещений. В случае же нестационарных связей сравнение выражений (4.2) и (4.3) показывает, что 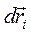не принадлежит этому множе­ству. Мы в дальнейшем считаем термины «виртуальный» и «возможный» синонимами, так как второй достаточно хорошо передает содержание французского слова virtuel. Сказанное о вектор-радиусе распространяется на любую функцию обобщенных координат и времени 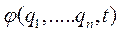. Дифферен­циал ее - это приращение функции в процессе движении за проме­жуток времени dt:

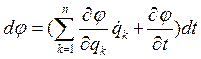
а вариация

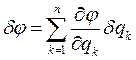
- бесконечно малое изменение, обусловленное переходом в фикси­рованный момент времени к бесконечно близкой конфигурации системы.

Рассмотренный в этом параграфе способ варьирования, заключаю­щийся в сравнении конфигураций системы, допускаемых связями, и фиксированный момент времени t, называется синхронным варьированием. Можно рассмотреть более общую операцию асинхронного варьирования, когда истинная конфигурация в момент t сравнивается с бесконечно близкой, допускаемой связями в момент 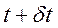, отлич­ный от t.

В механике Лагранжа основным понятием являются возможные перемещения, т.е. любые бесконечно малые перемещения системы, допускаемые связями, которые есть вариации координат или функций. Как указывалось выше дифференциал функции и вариация функции не одно и тоже. Уже само понятие вариация, очевидно, относится к особому методу вычисления, которое и носит название вариационное исчисление, о нём и пойдёт речь ниже.

Кроме задач определения экстремальных значений функций одной или нескольких переменных в технике, экономике и в раз­личных областях науки нередко приходится иметь дело с нахож­дением минимальных или максимальных значений величин осо­бого типа, которые называются функционалами.

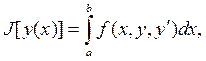
Приведем несколько примеров. Функционалом является дли­на 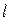кривой, соединяющей две точк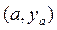и и 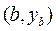на плоско­сти. Как известно, длина кривой на плоскости, заданной функцией у(х), определяется формулой

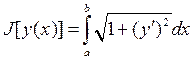
и, действительно, зависит от функции у(х). Отметим здесь, что функционалом является и длина пространственной кривой. Примером несколько иного типа является время движения управляемого объекта, зависящее как от формы траектории, так и от управляющего воздействия.

Вариационное исчисление изучает методы, с помощью кото­рых могут быть найдены минимальные или максимальные зна­чения функционалов. Задачи, в которых нужно найти минимум или максимум функционала, называются вариационными зада­чами. Многие законы физики сводятся к утверждению, что некото­рый функционал в изучаемом процессе имеет максимум или ми­нимум. В таком виде эти законы носят название вариационных принципов физики. В качестве примеров можно привести прин­цип наименьшего действия Гамильтона—Остроградского в меха­нике, принцип Ферма в оптике, различные вариационные прин­ципы классической и релятивистской теории поля и многие другие законы физики.

Начало созданию вариационного исчисления положили ис­следования решений задачи о брахистохроне, сформулированной И.Бернулли (1667—1748 гг.) в 1696 году. Он предложил математикам задачу о линии быстрейшего ската. В ней надо найти соединяющую две точки не лежащую на одной вертикали линию, обладающую тем свойством, что точка скатится из точки 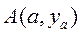в точку 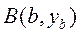за кратчайшее время. Оказалось, что линией быстрейшего ската оказалась циклоида.

Вариационное исчисле­ние оформилось в самостоятельную математическую дисциплину со своими методами исследования благодаря фундаментальным работам действительного члена Петербургской Академии наук Леонарда Эйлера (1707—1783 гг.). Л. Эйлера можно считать созда­телем вариационного исчисления.

В чём разница нахождения экстремума гладкой функции одной переменной и экстремума функционала вида 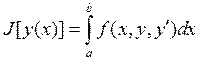. Для читателя незнакомого с дифференциальным исчислением можно предложить такой способ: взять некоторое значение координаты 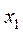и сосчитать 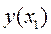, затем взять 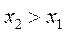и определить 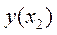. Если 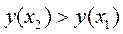, то мы на правильном пути. Берём следующее значение 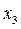и продолжаем наши вычисления до тех пор, пока не достигнем максимума функции. Для читателя, знакомого с дифференциальным исчислением, максимум функции, если он существует, определяется из условия равенства нулю первой производной заданной функции. Совсем иное найти непрерывную функцию у(х), удовлетворяющую граничным условиям 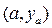и 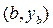, которая сообщает, например, минимум указанного выше функционала. Здесь уже надо рассматривать различные функции, отличающиеся друг от друга. Для читателя незнакомого с вариационным исчислением можно предложить такой способ: взять некоторую функцию 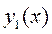и сосчитать интеграл 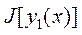. Возьмём новую функцию 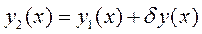, мало отличающуюся от 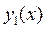и снова сосчитаем интеграл 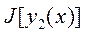. Если 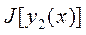< 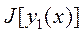, то можно перейти к следующему приближению и т.д. Правда, в этом случае неизвестно, когда надо остановиться. Для читателя, знакомого с вариационным исчислением, минимум функционала, если он существует, определяется из условия равенства нулю первой вариации заданного функционала. Но в отличии от максимума функции, который определятся нахождением одной точки, первая вариация функционала приводит к уравнению Эйлера

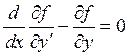(4.4)

после подстановки функции 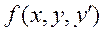в это уравнение получаем дифференциальное уравнение второго порядка, уравнение экстремалей, решение которого, если оно существует, и даёт искомую кривую у(х). Возможным перемещениям можно дать более простую интерпретацию, если рассмотреть пример, не имеющий отношения к теоретической механике. Пусть известна начальная точка А (Санкт-Петербург) и конечная точка В (к примеру, Петропавловск на Камчатке). Аналогом функционала здесь будет функция цели: маршрут с максимумом впечатлений и удовольствий. Автор предоставляет читателю самому рассмотреть различные варианты (возможные перемещения) маршрута. В конце концов, читатель из всех возможных вариантов выбирает действительный маршрут. Но при выборе маршрута могут возникнуть некоторые ограничения, к примеру, время путешествия, что, естественно, приведёт к выбору другого маршрута, к другим вариантам (возможным перемещениям); свобода выбора стала меньше (число степеней свободы меньше). Ну а если рассмотреть ещё и финансовые ограничения, то может случиться, что осуществить это путешествие просто невозможно (случай, когда решения не существует). Таким образом, возможные перемещения – это варианты перебора, функционал – функция цели, свобода выбора – число степеней свободы, действительное перемещение – выбранный маршрут.

Задачей механики Лагранжа будет отыскание среди возможных перемещений таких, которые удовлетворяют выбранным критериям.