Качественные показатели зацепления
 Одним из качественных показателей зубчатой передачи является коэффициент перекрытия
Одним из качественных показателей зубчатой передачи является коэффициент перекрытия 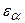 , равный
, равный 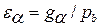 , где рв – шаг по основной окружности (расстояние между одноимёнными точками двух соседних зубьев, замеренное по дуге основной окружности). Коэффициент
, где рв – шаг по основной окружности (расстояние между одноимёнными точками двух соседних зубьев, замеренное по дуге основной окружности). Коэффициент 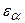 показывает сколько пар зубьев в среднем одновременно находится в зацеплении. Для прямозубой передачи обычно
показывает сколько пар зубьев в среднем одновременно находится в зацеплении. Для прямозубой передачи обычно 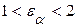 . Чем больше
. Чем больше 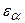 , тем более плавно и бесшумно работает передача.
, тем более плавно и бесшумно работает передача.
Другим качественным показателем является коэффициент скольжения, который учитывает влияние геометрии передачи и её кинематики на скольжение и износ профилей, скользящих друг по другу (рис. 74), что видно из картины скоростей. На этой картине:
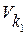 - скорость точки к первого колеса;
- скорость точки к первого колеса;
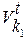 - проекция этой скорости на касательную к контактирующим профилям;
- проекция этой скорости на касательную к контактирующим профилям;

 и
и 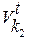 - тоже для колеса 2.
- тоже для колеса 2.
Скорость скольжения колеса 1 и 2 относительно друг друга равна:
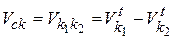 .
.
Коэффициенты скольжения колёс 1 и 2 равны:
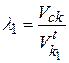 ;
; 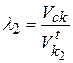 .
.
Эти коэффициенты равны нулю в полюсе (точка Р) и увеличиваются с удалением от него по линии зацепления.
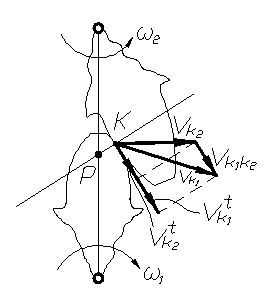
рис. 74
Таким образом, чем длиннее линия зацепления, (то есть, чем больше коэффициент перекрытия 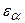 ), тем больше скольжение и износ профилей зубьев.
), тем больше скольжение и износ профилей зубьев.
8.8. Основные параметры зубчатых колёс
 Основными параметрами зубчатого колеса являются (рис. 75):
Основными параметрами зубчатого колеса являются (рис. 75):
рис. 75
z – число зубьев;
ra – радиус (диаметр) окружности
выступов;
rf – радиус (диаметр) окружности
впадин;
rb - радиус (диаметр) основной окружности;
r - радиус (диаметр) делительной окружности, т. е. окружности, которая является начальной в станочном зацеплении колеса с режущим инструментом;
р – шаг по делительной окружности;
h – высота зуба, равная h=ha+hf, где:
ha – высота головки зуба;
hf – высота ножки зуба;
m – модуль зацепления, определяемый из условия:
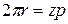 , т. е.
, т. е. 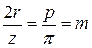 (измеряется в мм).
(измеряется в мм).
Величина m стандартизирована, а делительная окружность является окружностью стандартного модуля.
Обычно размеры зубчатого колеса и зубьев выражаются через m.
Так, например: 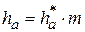 , где
, где 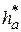 - коэффициент высоты головки зуба;
- коэффициент высоты головки зуба;
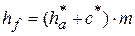 , где
, где 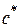 - коэффициент радиального зазора;
- коэффициент радиального зазора;
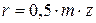 ;
; 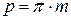 ;
; 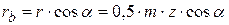 , где α – угол исходного контура режущего инструмента.
, где α – угол исходного контура режущего инструмента.
Обычно для стандартных зубчатых колёс: 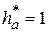 ;
; 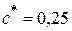 ; α=20º.
; α=20º.
8.9. Методы нарезания зубчатых колёс
Существует два принципиально различных метода нарезания:
1) метод копирования; 2) метод обкатки.
В первом случае впадина зубчатого колеса фрезеруется на универсальном фрезерном станке фасонными дисковыми или пальцевыми фрезами, профиль которых соответствует профилю впадины (рис. 76). Затем заготовку поворачивают
 на угол 360º/Z и нарезают следующую впадину. При этом используется делительная головка, а также имеются наборы фрез для нарезания колёс с различным модулем и различным числом зубьев. Метод непроизводителен и применяется в мелкосерийном и единичном производстве.
на угол 360º/Z и нарезают следующую впадину. При этом используется делительная головка, а также имеются наборы фрез для нарезания колёс с различным модулем и различным числом зубьев. Метод непроизводителен и применяется в мелкосерийном и единичном производстве.
рис. 76
Второй метод обката или огибания может производиться с помощью инструментальной рейки (гребёнки) на зубострогальном станке; долбяком на зубодолбёжном станке или червячной фрезой на зубофрезерном станке. Этот метод высокопроизводителен и применяется в массовом и крупносерийном производстве. Одним и тем же инструментом можно нарезать колёса с различным числом зубьев. Нарезание с помощью инструментальной рейки имитирует реечное зацепление (рис. 77, а), где профиль зуба образуется как огибающая последовательных положений профиля инструмента, угол исходного контура которого α=20º (рис. 77, б). Зацепление между режущим инструментом и нарезаемым колесом называется станочным. В станочном зацеплении начальная окружность всегда совпадает с делительной.
Самым производительным из рассмотренных методов является зубофрезерование с помощью червячных фрез, которые находятся в зацеплении с заготовкой по аналогии с червячной передачей (рис. 77, в).
При нарезании долбяком осуществляется его возвратно поступательное движение при одновременном вращении. Фактически при этом осуществляется зацепление заготовки с инструментальным зубчатым колесом – долбяком (рис. 77, г). Этот метод чаще всего используется при нарезании внутренних зубчатых венцов.
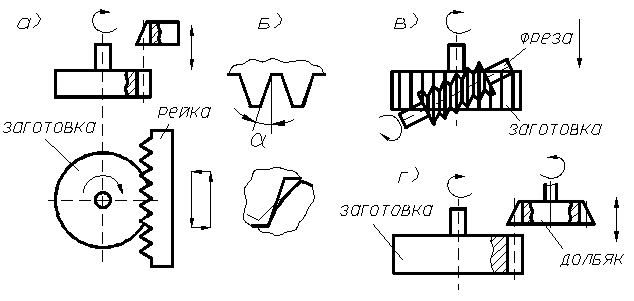
рис. 77
Все рассмотренные методы используются для нарезания цилиндрических колёс как с прямыми, так и с косыми зубьями.
8.10. Корригирование зубчатых колёс
 При нарезании колёс режущий инструмент можно располагать ближе к заготовке или дальше от неё. Положение инструмента определяется расстоянием между делительной окружностью колеса и так называемой модульной прямой рейки, проходящей через середину высоты зуба режущего инструмента (рис.78).
При нарезании колёс режущий инструмент можно располагать ближе к заготовке или дальше от неё. Положение инструмента определяется расстоянием между делительной окружностью колеса и так называемой модульной прямой рейки, проходящей через середину высоты зуба режущего инструмента (рис.78).
рис. 78
В зависимости от положения рейки по делительной окружности может перекатываться без скольжения либо модульная прямая рейки, либо начальная прямая, отстоящая от модульной прямой на величину смещения “b”, которое называется сдвигом или коррекцией, а коэффициент χ (хи), равный χ=b/m, называется коэффициентом смещения инструмента. Если инструмент смещён от нарезаемого колеса, то χ считается положительным (положительная коррекция), а если – к центру колеса, то χ отрицателен (отрицательная коррекция). При χ=0 нарезаемое колесо называется нормальным (нулевым). Толщина зуба и ширина впадины такого колеса по делительной окружности равны.
При положительной коррекции увеличивается прочность зуба, но уменьшается длина линии зацепления, а следовательно и коэффициент перекрытия 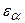 . При отрицательной коррекции – обратный эффект, т. е. увеличивается плавность и бесшумность работы передачи, но прочность зуба уменьшается.
. При отрицательной коррекции – обратный эффект, т. е. увеличивается плавность и бесшумность работы передачи, но прочность зуба уменьшается.
Зацепление двух зубчатых колёс характеризуется суммарным коэффициентом коррекции χΣ=χ1+χ2, причём возможны три случая:
1) χΣ=0 при χ1=χ2=0, когда в зацеплении находятся два нулевых зубчатых колеса (нулевое зацепление);
2) χΣ=0 при χ1=-χ2, когда в зацеплении находятся два корригированных зубчатых колеса, коэффициенты коррекции которых равны по величине и противоположны по знаку (равносмещённое зацепление с высотной коррекцией);
3) χΣ≠0, когда в зацеплении находятся два корригированных колеса, имеющих:
а) χΣ>0 – положительное неравносмещённое зацепление с угловой коррекцией;
б) χΣ<0 - отрицательное неравносмещённое зацепление с угловой коррекцией.
В первых двух случаях (χΣ=0) делительные окружности совпадают с начальными, угол зацепления 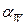 равен углу исходного контура рейки
равен углу исходного контура рейки 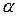 и межосевое расстояние равно
и межосевое расстояние равно 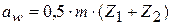 , в отличие от неравносмещённого зацепления, где делительные и начальные окружности не совпадают,
, в отличие от неравносмещённого зацепления, где делительные и начальные окружности не совпадают, 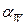 ≠
≠ 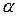 , а межосевое расстояние равно:
, а межосевое расстояние равно: 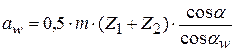 , с учётом того, что
, с учётом того, что
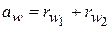 при
при 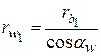 ;
; 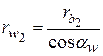 и
и
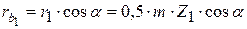 ;
; 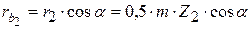 .
.
8.11. Наименьшее число зубьев зубчатых колёс. Подрезание и заострение зубьев
При нарезании нулевых колёс с малым числом зубьев может возникнуть явление врезания головок зубьев режущего инструмента в ножки зубьев колеса. Это явление называется подрезанием зуба. При этом уменьшается его прочность и увеличивается износ рабочей части зуба (рис. 79).

рис. 79
Согласно свойствам эвольвентного зацепления точки контакта зубьев эвольвентного профиля совпадают с линией NP, начиная с точки N (рис. 80), то есть высота прямолинейной части головки зуба режущего инструмента (рейки) 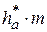 должна быть меньше отрезка PF, иначе часть головки зуба рейки будет контактировать с заготовкой (нарезать её) не по эвольвенте.
должна быть меньше отрезка PF, иначе часть головки зуба рейки будет контактировать с заготовкой (нарезать её) не по эвольвенте.
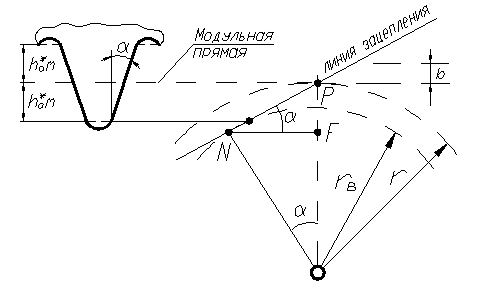
рис. 80
Так как 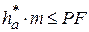 , а
, а 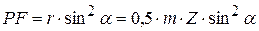 , то
, то
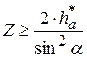 и
и 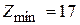 при стандартных значениях
при стандартных значениях 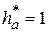 ;
; 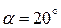 .
.
Для исключения подреза при Z<Zmin необходимо сместить инструмент от центра заготовки (положительная коррекция) так, чтобы 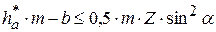 , т. е.
, т. е. 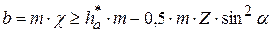
или с учётом того, что 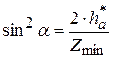 , получим при
, получим при 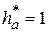 коэффициент коррек-
коэффициент коррек-
ции 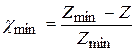 . Эта величина χ определяет нижний предел коэффициента коррекции.
. Эта величина χ определяет нижний предел коэффициента коррекции.
Если увеличивать коэффициент χ, то толщина зуба Sa у вершины (рис. 79) будет уменьшаться и при некотором χmax наступит заострение зуба (Sa=0). Опасность заострения наиболее велика у колёс с малым числом зубьев (Z<15). Для предотвращения разрушения заострённого зуба коэффициент смещения χ назначают с расчётом, чтобы Sa≥0,2m.
8.12. Выбор расчётных коэффициентов смещения для передач внешнего зацепления
При назначении коэффициентов смещения χ1 и χ2 для любой передачи должны выполняться три условия:
1) отсутствие подрезания;
2) отсутствие заострения;
3) непрерывность зацепления.
 Первое условие выполняется при
Первое условие выполняется при 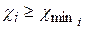 (
( 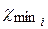 определяются из условия отсутствия подреза). Второе и третье условия выполняются при ограничении верхних пределов
определяются из условия отсутствия подреза). Второе и третье условия выполняются при ограничении верхних пределов 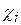 величинами
величинами 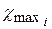 с учётом возможности заострения зубьев и уменьшения коэффициента перекрытия
с учётом возможности заострения зубьев и уменьшения коэффициента перекрытия 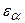 до величины
до величины 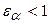 . То есть при выборе
. То есть при выборе 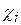 необходимо чтобы
необходимо чтобы 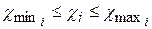 , где
, где 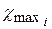 для каждого из колёс берётся наименьшим из значений, учитывающих заострение зуба и снижения
для каждого из колёс берётся наименьшим из значений, учитывающих заострение зуба и снижения 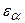 до величины
до величины 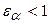 .
.
Внутри указанных диапазонов χ назначаются так, чтобы по возможности улучшить качественные показатели передачи (прочность, износостойкость, плавность хода).
Для передачи можно построить область допустимых значений коэффициентов смещения в координатах χ1 и χ2 , которая называется блокирующим контуром. Допустимые значения χ1 и χ2 расположены внутри контура (рис. 81). Для каждой передачи можно построить свой контур. Такие блокирующие контуры для различных передач имеются в справочной литературе.
рис. 81
8.13. Цилиндрические колёса с косыми зубьями и их особенности
Образование косозубого колеса можно представить, если взять цилиндрическое прямозубое колесо и сообщить ему крутильную деформацию. При этом угол скручивания, образованный осью колеса и винтовой линией, является углом наклона винтовой линии βº.
Цилиндрические колёса с косыми зубьями применяются при передаче вращения между параллельными и перекрещивающимися осями. В передаче с параллельными осями углы βº обоих колёс равны по величине и противоположны по направлению при внешнем зацеплении и одинаковы по направлению при внутреннем зацеплении. Угол βº (рис. 82, а) называется углом наклона зубьев по делительному цилиндру радиуса r. С другими соосными цилиндрами, начальным (rw) и основным (rb) винтовая поверхность зуба образует, соответственно, углы 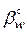 и
и 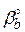 (рис. 82, а). Шаг винтовой линии равен:
(рис. 82, а). Шаг винтовой линии равен:
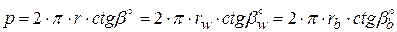 .
.
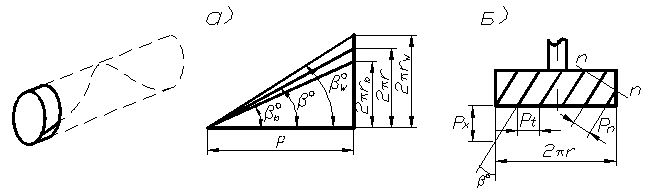
рис. 82
В косозубом колесе различают торцовый mt, нормальный mn и осевой mx модули, причём стандартное значение имеет нормальный модуль mn, соответствующий размерам зуба, замеренным по нормали nn к его оси (рис. 82, б), что объясняется установкой режущего инструмента. Аналогично различают торцовый pt, нормальный pn и осевой px шаг (рис. 82, б), связь между которыми определяется формулами:
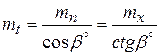 ;
; 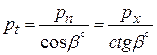 .
.
Большим достоинством зацеплений с косыми зубьями является возможность получения малогабаритных передач. Так, если для прямозубого колеса 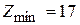 , то для косозубого
, то для косозубого 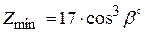 . В экспериментальных конструкциях
. В экспериментальных конструкциях 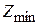 доводят до трёх и менее зубьев. Кроме того, увеличивается коэффициент перекрытия, доходя до 10 и выше, что также повышает нагрузочную способность и позволяет уменьшить габариты передачи. Недостатком является возникновение дополнительных осевых усилий, нагружающих подшипники. Этот недостаток устраняется в шевронных передачах.
доводят до трёх и менее зубьев. Кроме того, увеличивается коэффициент перекрытия, доходя до 10 и выше, что также повышает нагрузочную способность и позволяет уменьшить габариты передачи. Недостатком является возникновение дополнительных осевых усилий, нагружающих подшипники. Этот недостаток устраняется в шевронных передачах.
Дата добавления: 2015-12-29; просмотров: 3482;
