Основная теорема зацепления (теорема Виллиса)

Для постоянства передаточного отношения при зацеплении двух профилей зубьев необходимо, чтобы радиусы начальных окружностей зубчатых колёс, перекатывающихся друг по другу без скольжения, оставались неизменными. Если рассмотреть обращённое движение начальных окружностей, когда всей системе задана угловая скорость ( 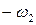), то второе колесо будет условно неподвижным и точка Р является мгновенным центром относительного вращения колёс (рис. 70,а). Эта точка, называемая полюсом зацепления, где контактируют начальные окружности, делит межцентровое расстояние на отрезки, обратно пропорциональные угловым скоростям, т. к.

.

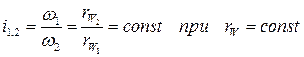Рассмотрим обращённое движение профилей зубьев зубчатых колёс (рис. 70, б).

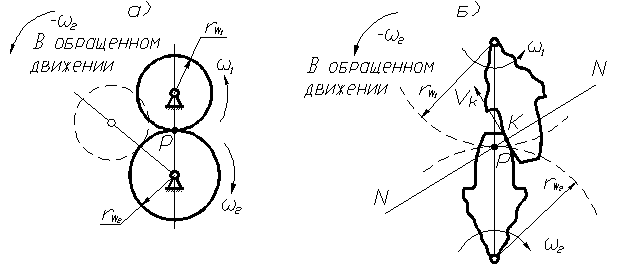
рис. 70

Точка контакта зубьев (точка к), принадлежащая первому колесу, вращается вокруг точки Р, которая будет мгновенным центром скоростей. Скорость 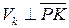и совпадает с общей касательной к профилям в точке к при условии постоянства этого контакта.

рис. 71

В противном случае постоянного контакта не будет, так как появится составляющая 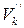и профили разомкнутся (рис. 71). Так как рассматривается произвольное положение зубьев, то можно сформулировать теорему.

Нормаль NN к касающимся профилям зубьев, проведённая через точку их касания, делит межцентровое расстояние на части, обратно пропорциональные угловым скоростям.

Эта теорема, сформулированная Виллисом в 1841 г., определяет основной закон зацепления профилей, которые не могут быть произвольными, а должны быть специально подобраны.

8.5. Эвольвента и её свойства

Наибольшее применение получили эвольвентные зубчатые передачи с профилем зубьев, очерченным по эвольвенте (рис. 72).

Эвольвентой круга называется траектория точки, лежащей на прямой, которая перекатывается без скольжения по окружности радиуса r_в, называемой основной.

рис. 72

Эвольвента имеет следующие свойства:

1) начинается с основной окружности;

2) нормаль к эвольвенте является касательной к основной окружности;

3) радиус кривизны эвольвенты в каждой её точке лежит на нормали к эвольвенте в этой точке.

Основная окружность представляет собой геометрическое место центров кривизны эвольвенты и является её эволютой.