Расчет резьбовых соединений, нагруженных отрывающими силами и моментами
Расчет соединений при действии центральной отрывающей силы. При действии центральной отрывающей силы F на затянутое соединение, только часть ее 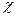 F дополнительно нагружает винты, а остальная часть (1-
F дополнительно нагружает винты, а остальная часть (1- 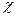 )F идет на разгрузку стыка (
)F идет на разгрузку стыка ( 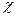 - коэффициент осн. нагр.).
- коэффициент осн. нагр.).
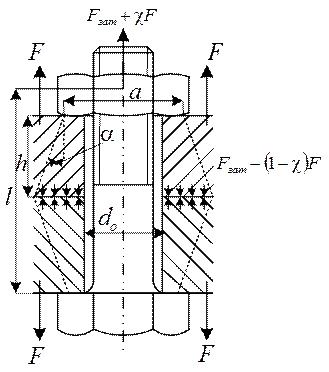
Задача о распределении нагрузки между винтом и стыком является статически неопределимой и решается с помощью условия совместности перемещений.
Очевидно, что под действием внешней нагрузки в пределах до раскрытия стыка винт удлиняется настолько, насколько уменьшается сжатие деталей. Это условие запишется так:

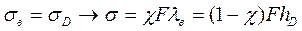
Отсюда: 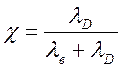 ; Податливость винта
; Податливость винта 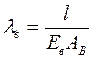 .
.
Точнее определяется 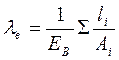 . Податливость винта определяют в предположении, что деформация распространяется на так называемые конусы давления. На основе опытов принимают tg
. Податливость винта определяют в предположении, что деформация распространяется на так называемые конусы давления. На основе опытов принимают tg 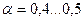 (иногда заменяют полым цилиндром при h≤1,5 а).
(иногда заменяют полым цилиндром при h≤1,5 а).
Податливость соединения при tg 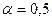 .
.
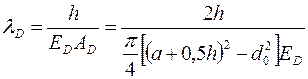 .
.
Более общая зависимость:
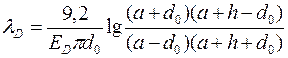
Для винтовых соединений с центральной отрывающей нагрузкой этот расчет позволяет непосредственно определить потребную силу начальной затяжки.
Согласно условию сохранения плотности стыка силы затяжки одного винта в соединении с z винтами:

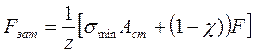
Осевая сила, действующая на затянутый винт после приложения внешней нагрузки, F1:
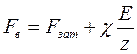
Расчетная нагрузка с учетом крутящего момента затяжки:
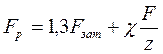
Расчет соединений при действии нагрузки в плоскости симметрии.
Предполагаем, что фланцы жесткие и винты распределены по стыку достаточно равномерно.
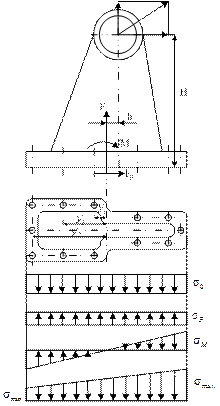
Внешнюю нагрузку приводим к отрывающей силе, приложенной в центре массы стыка, и к опрокидывающему моменту М. Сдвигающие силы в стыке, обычно, воспринимаются штифтами или шпонками и поэтому не рассматриваются.
Принимаем, что F и М распределяются между стыком и винтами, как в статически неопределяемых системах, обратно пропорционально их податливости:
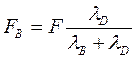 ;
; 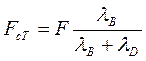
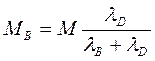 ;
; 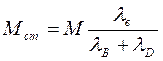
Исходным условием расчета является не раскрытие стыка во избежании контактной коррозии и понижения жесткости. Для обеспечения достаточной жесткости ответственных деталей 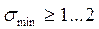 МПа; Согласно условию не раскрытия стыка
МПа; Согласно условию не раскрытия стыка 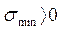 .
.
Деформации в стыке при жестких на изгиб фланцах распределяются по линейному закону. Поэтому, если справедлив закон Гука, то напряжения также распределяются по линейному закону и могут быть подсчитаны по формулам для неравномерного сжатия.
Напряжения алгебраически складываются из напряжений в стыке от Fзат, Fст, Мст:

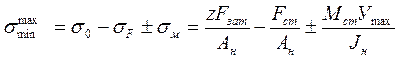 .
.
Если F сжимает стык, то знак минус меняется на плюс.
Обычно площадь стыка больше площади сечения винтов. В этом случае расчет стыка можно вести по полной силе F и моменту М, но по номинальной площади А и моменту инерции J площади стыка без вычета площади отверстий:
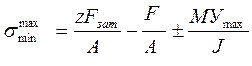
При жестких фланцах нагрузка по винтам от силы Fв распределяется равномерно. Нагрузка и напряжения в винтах от момента распределяются пропорционально расстоянию от нейтральной оси, т.е. по закону, что и при изгибе. Поэтому при расчете напряжений в винтах от момента можно пользоваться формулами для расчета напряжений от изгиба.
Расчет ведут для винтов наиболее нагруженного ряда напряжений в этих винтах:
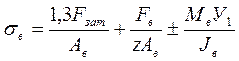
где JВ≈∑АвУ2i
Расчет винтов крепления крышек цилиндров, находящихся под внутренним давлением.
Расчет производят по условию герметичности соединения.
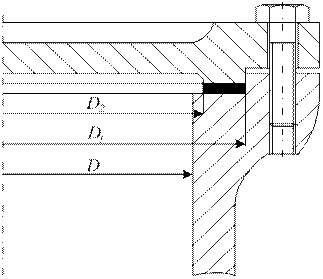
Полная сила, растягивающая винты, при действии расчетного давления Р, складывается из силы давления среды на крышку и остаточной силы, потребной для сжатия прокладки:
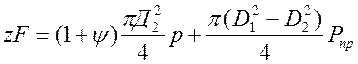
где 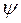 - коэффициент, учитывающий возможное повышение давления (
- коэффициент, учитывающий возможное повышение давления ( 
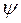 =0,2). Рпр для мягких прокладок (2…2,5)р, а для металлических прокладок 3,5 р.
=0,2). Рпр для мягких прокладок (2…2,5)р, а для металлических прокладок 3,5 р.
Винты, подверженные переменной нагрузке. Наиболее характерным случаем действия переменных внешних нагрузок на винтовые соединения является действие нагрузок, изменяющихся от 0 до F.
Переменная нагрузка F распределяется между винтом и затянутым стыком, причем на винт приходится доля, равная 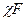 , где
, где 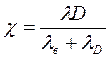 .
.
Таким образом, амплитуда напряжений в винте:
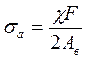 .
.
Среднее напряжение:
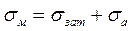 .
.
Максимальное напряжение:
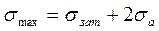
В расчетах проверяют запас прочности по амплитудам и по максимальным напряжениям:
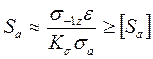 ;
; 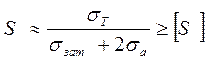 ,
,
где 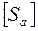 =2,5…4;
=2,5…4; 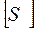 = 1,25…2,5
= 1,25…2,5
Дата добавления: 2015-12-29; просмотров: 3291;
