Осаждение (всплывание) твердых частиц в покоящейся жидкости
Падение (осаждение) твердых тел в покоящейся жидкости может быть:
• свободное, когда на падающее тело не оказывают влияния соседние твердые тела и стенки емкости, в которой происходит осаждение;
• стесненное, когда, наоборот, на осаждение тела влияют соседние тела и стенки емкости;
• стесненное однородных по крупности, плотности и форме частиц;
• стесненное неоднородных частиц.
Движение твердых частиц при осаждении в покоящейся или сравнительно медленно движущейся жидкости является, как правило, равномерным. Скорость равномерного движения твердой частицы 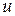 в достаточно большом объеме покоящейся жидкости (свободное осаждение) получила название гидравлической крупности
в достаточно большом объеме покоящейся жидкости (свободное осаждение) получила название гидравлической крупности 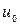 .
.
Возьмем твердую частицу сферической формы диаметром d и массой 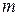 , которая осаждается в большом объеме воды. Применительно к движущейся частице можно написать уравнение равновесия
, которая осаждается в большом объеме воды. Применительно к движущейся частице можно написать уравнение равновесия
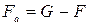 , (4.168)
, (4.168)
где 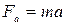 ; G - сила тяжести частицы с учетом ее взвешивания в воде; F - сила полного сопротивления движению (сила лобового сопротивления).
; G - сила тяжести частицы с учетом ее взвешивания в воде; F - сила полного сопротивления движению (сила лобового сопротивления).
В связи с тем что движение считается равномерным, ускорение частицы равно нулю: 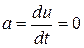 . Следовательно, можно написать: G = F.
. Следовательно, можно написать: G = F.
Вес частицы сферической формы с учетом архимедовой силы
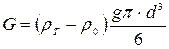 , (4.169)
, (4.169)
где 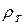 - плотность твердой частицы;
- плотность твердой частицы; 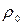 - плотность воды.
- плотность воды.
Силу лобового сопротивления при падении частицы определим по формуле (4.169)
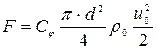 (4.170)
(4.170)
где 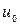 - скорость равномерного движения частицы в воде.
- скорость равномерного движения частицы в воде.
Приравняв значения этих сил и сделав некоторые преобразования, получим значение гидравлической крупности, зависящее от коэффициента лобового сопротивления 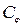 :
:
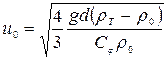 . (4.171)
. (4.171)
В случае когда 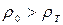 , будет происходить всплывание частиц, и скорость всплывания
, будет происходить всплывание частиц, и скорость всплывания
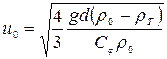 (4.172)
(4.172)
Однако недостатком формул (4.171) и (4.170) является присутствие в них коэффициента лобового сопротивления 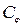 , имеющего сложные зависимости от числа Рейнольдса и ряда других факторов.
, имеющего сложные зависимости от числа Рейнольдса и ряда других факторов.
При движении весьма малых частиц (Re<1) уравнение (4.171) в соответствии с равенством 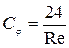 приобретает вид уравнения Стокса:
приобретает вид уравнения Стокса:
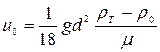 . (4.173)
. (4.173)
Некоторая степень неточности при определении 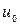 имеет место в связи с тем, что частицы имеют форму, несколько отличную от сферической. Поэтому берется осредненное значение диаметра частицы, т.е. эквивалентный ее диаметр
имеет место в связи с тем, что частицы имеют форму, несколько отличную от сферической. Поэтому берется осредненное значение диаметра частицы, т.е. эквивалентный ее диаметр
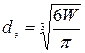 , (4.174)
, (4.174)
где 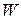 - объем твердой частицы, который соответствует объему шара диаметром
- объем твердой частицы, который соответствует объему шара диаметром 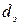 .
.
Дата добавления: 2015-12-29; просмотров: 1258;
