Регулирующая арматура. Задвижка. Для односторонней задвижки круглой трубы сопротивление зависит от степени ее открытия, т.е
Задвижка. Для односторонней задвижки круглой трубы сопротивление зависит от степени ее открытия, т.е. от отношения 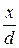 (рис. 4.23). В результате малого открытия происходит отрыв потока от сегмента задвижки и стенок с образованием водоворотной области, а на поверхности раздела области с потоком происходит пульсация скоростей и интенсивное вихреобразование, приводящее к массообмену частицами жидкости.
(рис. 4.23). В результате малого открытия происходит отрыв потока от сегмента задвижки и стенок с образованием водоворотной области, а на поверхности раздела области с потоком происходит пульсация скоростей и интенсивное вихреобразование, приводящее к массообмену частицами жидкости.
В табл. 4.2 приведены значения коэффициента 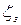 в зависимости от степени открытия
в зависимости от степени открытия 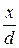 .
.
Таблица 4.2 - Значения 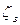 в зависимости от степени открытия
в зависимости от степени открытия 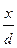
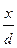
| 0,125 | 0,25 | 0,375 | 0,5 | 0,625 | 0,75 | 0,875 | ||
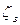
| 0,05 | 0,07 | 0,26 | 0,80 | 2,10 | 5,50 | 17,0 |
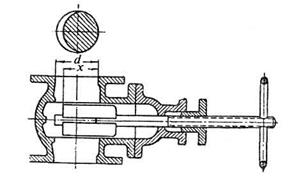
Рис. 4.23. Задвижка
Пробковый кран, вентили. Сопротивление пробкового крана напрямую зависит от угла открытия крана 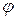 (рис. 4.24).
(рис. 4.24).
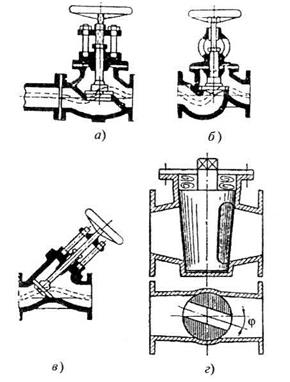
Рис. 4.24. Регулирующая арматура:
а - прямоточный вентиль; б - нормальный вентиль;
в - вентиль типа косва; г - пробковый кран
В табл. 4.3 приведены значения коэффициента местных сопротивлений крана 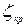 .
.
Таблица 4.3 - Значения 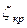 в зависимости от угла открытия
в зависимости от угла открытия 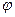
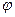
| |||||||
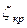
| 0,29 | 1,56 | 5,47 | 17,3 | 52,6 |
Значения коэффициентов местных сопротивлений вентилей (см. рис. 4.24) различной конструкции при полном их открытии следующие:
прямоточный - 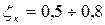 ;
;
нормальный - 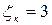 ;
;
с косым затвором (косва) - 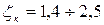 .
.
Тройники
Деталь трубы, в которой имеет место разделение или соединение потоков жидкости, называется тройником (рис. 4.25). При определении гидравлических потерь в тройниках принимается средняя скорость 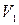 соответствующая расходу
соответствующая расходу 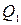 до разделения и
до разделения и 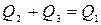 - после слияния.
- после слияния.
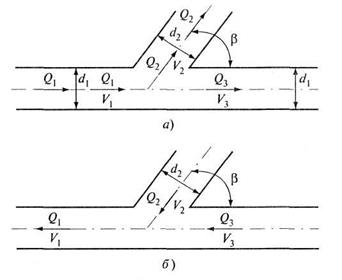
Рис. 4.25. Тройник: а - разделение потока; б - слияние потоков
Гидравлические потери напора возникают в результате соединения потоков жидкости или их разделения. Коэффициенты местных сопротивлений зависят от геометрии тройника, т.е. от угла 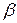 , соотношения диаметров
, соотношения диаметров 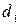 ,
, 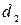 ,
, 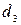 и отношения расходов
и отношения расходов 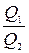 и
и 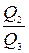 .
.
Коэффициенты местных сопротивлений 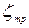 , получены в результате многочисленных опытов, их значения приведены в специальных справочниках [2, 4].
, получены в результате многочисленных опытов, их значения приведены в специальных справочниках [2, 4].
Пример 4.5
В трубопроводе диаметром 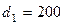 мм имеется внезапное сужение диаметром
мм имеется внезапное сужение диаметром 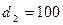 мм. Определить местные потери напора и коэффициент
мм. Определить местные потери напора и коэффициент 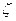 , отнесенный к узкой части трубопровода. Расход воды в трубопроводе
, отнесенный к узкой части трубопровода. Расход воды в трубопроводе 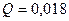 м3/с (см. рис. 4.19).
м3/с (см. рис. 4.19).
Коэффициент местных сопротивлений находим по формуле И. Идельчика (4.144):
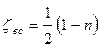 .
.
Отношение площадей живых сечений характеризуется величиной 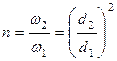 .
.
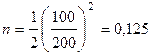 ,
,
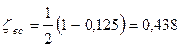 .
.
Средняя скорость в сужающей части трубы диаметром 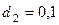 м
м 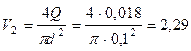 м/с.
м/с.
Потери напора
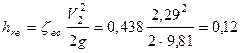 м.
м.
Пример 4.6
Для ограничения расхода воды в трубопроводе диаметром 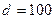 мм установлена диафрагма. Избыточные давления до диафрагмы и после нее постоянны и соответственно равны
мм установлена диафрагма. Избыточные давления до диафрагмы и после нее постоянны и соответственно равны 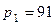 кПа и
кПа и 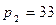 кПа. Определить необходимый диаметр отверстия диафрагмы d при условии, что расход
кПа. Определить необходимый диаметр отверстия диафрагмы d при условии, что расход 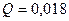 м3/с (см. рис. 4.21).
м3/с (см. рис. 4.21).
Потери напора на участке трубопровода, где установлена диафрагма, при скорости в трубопроводе 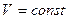 равны
равны
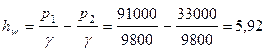 м.
м.
Средняя скорость в трубопроводе
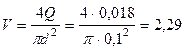 м/с.
м/с.
Коэффициент местных сопротивлений диафрагмы согласно формуле Вейсбаха
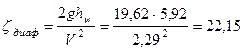 .
.
Коэффициент 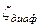 вычисляется по формуле А. Альтшуля (4.145)
вычисляется по формуле А. Альтшуля (4.145)
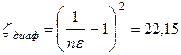 .
.
Коэффициент сжатия потока (4.143)
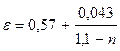 ,
,
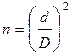 .
.
В первом приближении примем 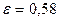 .
.
Преобразуем формулу (4.145) для определения 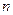 :
:
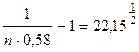 ;
; 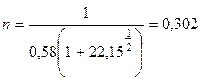 ;
;
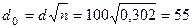 мм.
мм.
Уточним полученный диаметр отверстия, вычислив 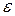 :
:
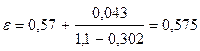 ;
;
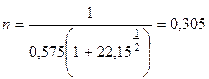 .
.
Диаметр отверстия диафрагмы после уточнения 
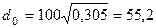 мм.
мм.
Дата добавления: 2015-12-29; просмотров: 1602;
