ПРЯМОЙ И НЕПРЯМОЙ ГИДРАВЛИЧЕСКИЕ УДАРЫ
В зависимости от соотношения фазы удара Т и времени закрытия затвора 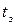 гидравлические удары разделяют на прямые (
гидравлические удары разделяют на прямые ( 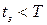 ) и непрямые (
) и непрямые ( 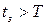 ).
).
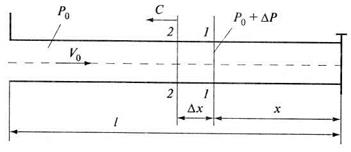
Рис. 5.18. К определению повышения давления в трубе при гидравлическом ударе
Рассмотрим движение жидкости в трубе постоянного сечения площадью 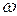 , на конце которой находится запорное устройство - затвор. Средняя скорость жидкости в трубе
, на конце которой находится запорное устройство - затвор. Средняя скорость жидкости в трубе 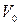 и давление
и давление 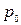 (рис. 5.18).
(рис. 5.18).
При резком закрытии затвора возникает гидравлический удар. Вначале масса жидкости, находящаяся в трубе, остановится, а волна повышения давления 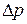 будет распространяться в обратную сторону от затвора со скоростью С. В момент времени t на расстоянии х (сечение 1-1) от затвора произойдет сжатие жидкости, т.е. фронт ударной волны будет находиться в этом сечении. За время
будет распространяться в обратную сторону от затвора со скоростью С. В момент времени t на расстоянии х (сечение 1-1) от затвора произойдет сжатие жидкости, т.е. фронт ударной волны будет находиться в этом сечении. За время 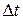 фронт волны переместится на расстояние
фронт волны переместится на расстояние 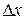 (сечение 2-2),
(сечение 2-2), 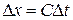 . Давление в сечении увеличится на
. Давление в сечении увеличится на 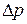 и станет равным
и станет равным  . Повышение давления будет распространяться со скоростью ударной волны С.
. Повышение давления будет распространяться со скоростью ударной волны С.
Для вывода формулы повышения давления 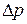 рассматривается объем жидкости в трубе между сечениями 1-1 и 2-2, масса которой
рассматривается объем жидкости в трубе между сечениями 1-1 и 2-2, масса которой 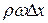 . Перед сечением 2-2 скорость жидкости равна скорости в трубе
. Перед сечением 2-2 скорость жидкости равна скорости в трубе 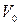 , а давление -
, а давление - 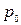 . На выделенном участке трубы длиной
. На выделенном участке трубы длиной 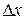 произойдет повышение давления на величину
произойдет повышение давления на величину 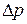 , которую можно определить, используя теорему количества движения. Количество движения для рассматриваемого объема до закрытия затвора
, которую можно определить, используя теорему количества движения. Количество движения для рассматриваемого объема до закрытия затвора
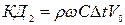 . (5.49)
. (5.49)
В сечении 1-1 после закрытия затвора скорость равна нулю и количество движения также равно нулю, т.е. 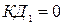 .
.
Изменение количества движения 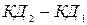 составит
составит
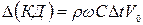 , (5.50)
, (5.50)
где  - площадь сечения трубы;
- площадь сечения трубы;  - плотность жидкости.
- плотность жидкости.
За этот же промежуток времени на выделенный объем действуют силы давления в рассматриваемых сечениях, импульс сил составит
 . (5.51)
. (5.51)
Приравняв значения количества движения 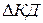 и импульса сил, получим
и импульса сил, получим
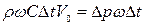 .
.
Отсюда повышение давления при гидравлическом ударе
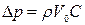 . (5.52)
. (5.52)
Уравнение (5.52) является формулой Н. Жуковского для определения повышения давления при прямом гидравлическом ударе.
 Формулу Жуковского можно представить не через повышение давления, а через дополнительный напор в трубопроводе:
Формулу Жуковского можно представить не через повышение давления, а через дополнительный напор в трубопроводе:
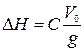 . (5.53)
. (5.53)
При непрямом гидравлическом ударе в момент возвращения ударной волны через неперекрытую часть сечения затвора успевает пройти некоторый расход со средней скоростью V. Это приводит к уменьшению величины повышения давления при гидравлическом ударе, и формула Н. Жуковского принимает вид
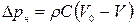 . (5.54)
. (5.54)
Можно считать, что скорость в трубе при постоянном закрытии затвора изменяется линейно, и это изменение выражается следующей зависимостью
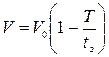 . (5.55)
. (5.55)
Подставив (5.55) в (5.54), получим выражение, по которому можно определить повышения давления  при непрямом гидравлическом ударе (
при непрямом гидравлическом ударе (  ):
):
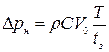 . (5.56)
. (5.56)
Таким образом, имеется линейная зависимость между давлением 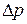 и
и 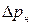
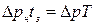 . (5.57)
. (5.57)
Используя формулу (5.48) для определения времени фазы удара Т, получим вместо (5.56) формулу для вычисления 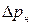
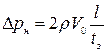 . (5.58)
. (5.58)
Согласно (5.58) значение давления при непрямом ударе в отличие от прямого удара зависит от длины трубопроводов и не зависит от скорости распространения ударной волны С.
Таким образом, для того чтобы уменьшить повышение давления в трубе, необходимо увеличить время закрытия затворов (задвижек)  .
.
Скорость распространения ударной волны, по Н. Жуковскому, равна
 , (5-59)
, (5-59)
где 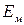 - модуль упругости материала стенки трубы;
- модуль упругости материала стенки трубы;  - модуль упругости жидкости в трубе.
- модуль упругости жидкости в трубе.
В случае абсолютно неупругих стенок труб  , скорость распространения ударной волны
, скорость распространения ударной волны
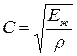 . (5.60)
. (5.60)
Формула (5.60) является формулой Ньютона для определения распространения звука в неограниченной жидкой среде.
Для воды при температуре 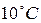 ,
, 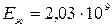 Па и плотности
Па и плотности  кг/м3 скорость звука
кг/м3 скорость звука 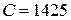 м/с.
м/с.
Таким образом, при движении воды по трубопроводу скорость распространения ударной волны, м/с,
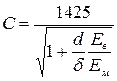 ,
,
где 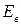 - модуль упругости воды.
- модуль упругости воды.
Соотношение модулей упругости воды 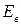 и материала стенок труб
и материала стенок труб 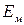 приводится в табл. 5.7
приводится в табл. 5.7
Таблица 5.7
| Материал стенки трубы | 
|
| Сталь | 0,01 |
| Чугун | 0,02 |
| Асбоцемент | 0,11 |
| Винипласт | 0,68 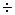 0,73 0,73
|
| Полиэтилен | 1 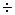 1,45 1,45
|
Дата добавления: 2015-12-29; просмотров: 945;
