Определение скорости выхода пара из каналов направляющего аппарата и рабочей решетки.

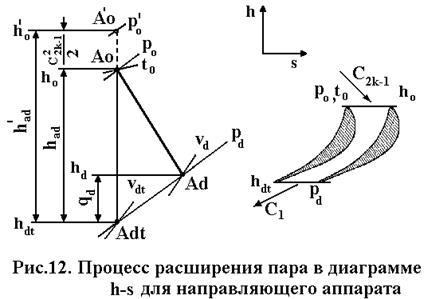Рассмотрим течение пара в решетке турбинных лопаток и поставим задачу: определить скорость пара на входе из решетки. В начале будем рассматривать неподвижную решетку направляющего аппарата, т.е. речь будет идти об «абсолютном» движении пара. Пусть рассматриваемая направляющая решетка (рис.12) относится к некоторой промежуточной k-ой ступени. Тогда перед этой ступенью расположена (k-1)-я ступень, и поток пара, выходящий из этой ступни со скоростью С_2(к-1), плавно входит в рассматриваемую направляющую решетку.

Пусть давление и температура пара перед решеткой соответственно равны Р₀и t₀.

При анализе процессов течения пара в паровых турбинах широко используются тепловые диаграммы водяного пара и, в частности, диаграмма h–s. Это связано с тем, что уравнение состояния водяного пара в достаточно простом виде отсутствует.

Обращаясь к диаграмме h–s (рис.12) на пересечении изобары Р₀ и изотермы t₀ можно найти точку А₀, характеризующую состояние пара перед решеткой и снять с диаграммы энтальпию пара h₀.

На входе в направляющий аппарат пар уже обладает некоторой кинетической энергией 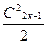. На тепловой диаграмме эта кинетическая энергия может быть показана только условно. Представим себе, что поток пара на входе в решетку изоэнтропийно (без трения) заторможен. Тогда его энтальпия увеличилась бы на величину 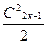. Отложив кинетическую энергию 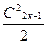вверх от точки А₀, получим точку 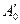, характеризующую параметры торможения потока – давление 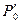, температура 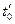и энтальпия .

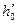Итак, поток пара, состояние которого определяется точкой А₀ диаграммы h–s, со скоростью 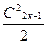входит в каналы направляющего аппарата. Рассматриваемое движение пара, введем допущения о том, что поток в каналах решетки одномерный и установившийся, а теплообмен с внешней средой отсутствует. Кроме того, вначале будем пренебрегать вязкостью пара; тогда трение в потоке отсутствует, и состояние пара будет изменяться по адиабате.

Такой процесс течения пара (без трения) условно будем называть теоретическим, а параметры этого процесса будем дополнительно обозначать индексом «t».

Пусть давление за решеткой равно Р_d. Проведя из точки А₀ адиабату до пересечения с изобарой Р_d (рис.12) можно на диаграмме h–s найти точку А_dt, определяющую состояние пара в конце теоретического процесса и снять в этой точке энтальпию h_dt. Теоретическую скорость пара на выходе из направляющего аппарата обозначим C_1t. Тогда уравнение энергии для входного и выходного сечений решетки запишется в виде:

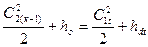(3.1)

Это уравнение показывает, что при отсутствии теплообмена полная удельная энергия потока, складывающаяся из кинетической 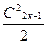и потенциальной h энергии не изменяется.

Разность энтальпий на входном и выходном сечениях решетки определяет тот запас потенциальной энергии, который может быть преобразован в направляющем аппарате в кинетическую энергию. Эту разность будем обозначать h_ad и называть адиабатным теплоперепадом в направляющем аппарате (в соплах):

h_ad=h₀-h_dt (3.2)

Тогда непосредственно из уравнения энергии (2.2.1) получим выражение для теоретической скорости выхода пара из решетки:

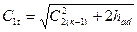(3.3)

Таким образом, на выходе из направляющего аппарата ступени поток пара приобретает скорость С_1t за счет освобождения некоторой части потенциальной энергии h_ad и за счет скорости на входе С_2(к-1).

Сумму входной кинетической энергии и адиабатного теплоперепада обозначают h'_ad и называют располагаемым теплоперепадом:

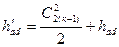(3.4)

Тогда формула для определения теоретической скорости истечения запишется в виде:

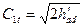(3.5)

Теплоперепады h_adи h'_ad могут быть показаны на диаграмме h-s (рис.12).

Формулы (2.2.3) и (2.2.5) определяют теоретическую скорость истечения. Однако на практике приходится иметь дело с реальным потоком пара, в котором действуют силы вязкости. Поэтому действительная скорость истечения пара С₁ будет несколько меньше теоретической. Для характеристики реального процесса течения пара в теории турбин вводится понятие коэффициента скорости φ, который определяется отношением действительной скорости истечения к теоретической:

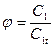(3.6)

Для определения величины коэффициента скорости φ следовало бы рассчитать течение в пограничном слое на поверхности лопаток и вычислить сопротивление трения и вихревое сопротивление решетки. В принципе такая задача может быть решена. Однако на практике величина коэффициента φ определяется опытным путем при продувках решеток турбинных лопаток на специальных газодинамических стендах. Для современных турбинных профилей направляющих аппаратов коэффициент φ обычно имеет порядок 0,95-0,97.

Таким образом, для определения действительной скорости выхода пара из направляющего аппарата ступени получим формулы:

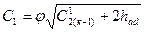(3.7)

или

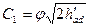(3.8)

Скорость входа пара в направляющий аппарат С_2(к-1) часто бывает пренебрежимо мала. Тогда адиабатный и располагаемый теплоперепады равны. В этом случае формула для определения скорости истечения записывается в виде

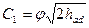(3.9)

Поставленная задача решена – мы определили скорость выхода пара из направляющего аппарата ступени. Для того чтобы, полностью характеризовать течение в направляющем аппарате необходимо определить состояние пара на выходе из решетки. С этой целью вводится понятие о потерях кинетической энергии при течении пара через решетку.

Если бы трение и другие сопротивления отсутствовали, то скорость пара на выходе из решетки была бы равна C_1t, а его удельная кинетическая энергия составляла бы 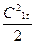. Это – максимальная кинетическая энергия, которая может быть получена при заданных условиях расширения пара. Поэтому энергия 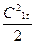называется располагаемой кинетической энергией.

В реальном потоке удельная кинетическая энергия на выходе из решетки составляет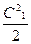

Потерей кинетической энергии в направляющем аппарате называется разность между располагаемой и действительной кинетической энергией на выходе из решетки. Иногда эту величину называют просто «потери энергии», опуская слово «кинетической». Применяя термин «потери энергии» следует иметь в виду, что речь идет именно о потерях кинетической энергии, и что эта энергия не исчезает безвозвратно, а приводит к повышению энтальпии пара.

Потери кинетической энергии в направляющем аппарате (в соплах) обозначаются через q_d. Согласно данному выше определению эти потери составляют:

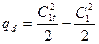(3.10)

Для характеристики относительной величины потерь энергии вводится понятие коэффициента потерьς_d, который определяется отношением потерянной кинетической энергии к располагаемой кинетической энергии:

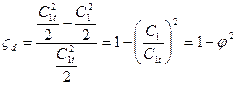(3.11)

С учетом определения коэффициента ς_d, выражение для потерь энергии может быть записано в виде:

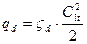(3.12)

или

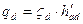(3.13)

Теперь можно определить действительное состояние пара за решеткой. Для теоретического процесса это состояние характеризовалось точкой А_dt диаграммы h-s, причем энтальпия пара в этой точке составляла h_dt. В реальном процессе потерянная кинетическая энергия q_d расходуется на преодоление трения и прочих сопротивлений решетки, что приводит к росту энтальпии пара. Поэтому действительная энтальпия пара за решеткой h_d будет равна:

h_d =h_dt+q_d (3.14)

На диаграмме h-s (рис.12) энтальпию h_d легко найти, отложив вверх от точки А_dt потерю q_d. Точка А_d, определяющая действительное состояние пара за направляющим аппаратом определяется пересечением изобары Р_d и линии постоянной энтальпии h_d=соnst. В точке А_d диаграммы h-s можно снять необходимые параметры пара, и в частности, удельный объем V_d. Таким образом, действительный процесс течения пара в направляющем аппарате изобразится на диаграмме h-s некоторой политропой А_оА_d (теоретический процесс – адиабата А_оА_dt), которая условно проводится прямой.