Дивергенция электрического поля.

С помощью теоремы Остроградского поверхностный интеграл в левой части теоремы Гаусса (5.4) можно преобразовать в интеграл по объему V , ограниченному поверхностью S: ∮ SE→⋅dS→ = ∫ V divE→dV. (6.1)

Результат преобразования называют теоремой Остроградского-Гаусса: ∫ V divE→dV = 4π ∫ V ρdV .

Поскольку она верна для любой области интегрирования V , в том числе и бесконечно малой, из неё следует равенство подынтегральных выражений слева и справа в каждой точке пространства: divE→ = 4πρ. (6.2)

Это дифференциальное уравнение является одним из основных уравнений электростатики; оно верно также для динамических явлений.

Теорему Остроградского (6.1) можно пытаться доказывать, отталкиваясь от какого-либо из определений оператора дивергенции div. Однако саму эту теорему можно рассматривать в качестве инвариантного определения div, не зависящего от выбора системы координат. Переходя в (6.1) к пределу V → 0, получаем: divE→ = limV →0 ∮ SE→⋅dS→ V. (6.3)

Вместо E→ здесь, как и в (6.1), может стоять любой другой вектор.

Покажем, как из (6.3) получается выражение для дивергенции в декартовых координатах. Рассмотрим небольшой параллепипед, образованный координатными плоскостями, как показано на рис. 1.12.

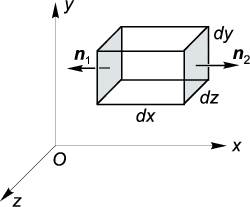
Рис. 1.12:

В пределах каждой грани параллелипипеда вектор E→ можно считать постоянным, поскольку затем размеры параллелипипеда будут устремлены к нулю. Тогда поверхностный интеграл по каждой грани равен произведению площади грани на нормальную (к этой грани) компоненту вектора E→. Например, для пары противоположных граней в координатных плоскостях x и x + dx имеем (Ex∣x+dx − Ex∣x)∣Sx∣, где ∣Sx∣ = dy dz — площадь каждой из граней. Знак минус перед вторым слагаемым в скобках здесь связан с тем, что нормаль к соответствующей грани направлена в отрицательном направлении оси x. Разлагая первое слагаемое в скобках в ряд Тейлора вокруг точки x с точностью до члена, линейного по dx, находим, что вклад этой пары граней в поверхностный интеграл равен (∂Ex∕∂x)V , где V = dxdy dz. Аналогичным образом вычисляется вклад двух других пар граней. После сокращения на V из (6.3) получаем: divE→ = ∂Ex ∂x + ∂Ey ∂y + ∂Ez ∂z . (6.4)