Общее решение уравнения Пуассона.

Если система зарядов сосредоточена в ограниченном объёме можно указать общее решение уравнения Пуассона (10.1). В соответствии с принципом суперпозиции скалярный потенциал системы точечных зарядов равен сумме потенциалов, создаваемых полем каждого заряда в отдельности: ϕ(r→) = ∑ j q ∣r→ −r→j∣. (11.1)

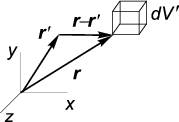
Рис. 1.23:

Переходя к непрерывному распределению зарядов этот результат можно представить в виде интеграла ϕ(r→) = ∫ V ρ(r′→)dV ′ ∣r→ −r′→∣, (11.2)

где r→, r′→ — радиусы-векторы точки наблюдения и элементарного объёма dV ′, соответственно (рис. 1.23). Интеграл распространяется на весь объём, где плотность зарядов ρ не равна нулю. Формулу (11.2) называют общим решением уравнения Пуассона. В теории она играет очень важную роль, но в практических вычислениях используется редко. Часто бывает удобнее использовать приближенные формулы, полученные на её основе.

Покажем теперь, как совершить обратный переход и из общего решения уравнения Пауссона (11.2) получить потенциал точечного заряда. Для этого необходимо признать необычные свойства функции плотности заряда ρ(r→): она равна нулю всюду, кроме точки, где расположен заряд, однако, будучи проинтегрированной по объему, даёт конечное значение заряда «точки». Таким свойствами обладает дельта-функция, введённая английским физиком Дираком. Математики относят её к классу обобщенных функций. Для одного заряда q, расположенного в точке r→j, положим ρ(r→) = q δ(r→ −r→j). (11.3)

Трехмерная δ-функция δ(r→ − ρ(r→j) обладает следующими свойствами:

δ(r→ −r→j) всюду, кроме точки r→ = ρ(r→j);

∫ f(r→)δ(r→ −r→j)dV = f(r→j), где f(r→) — любая непрерывная функция; в частности, если f ≡ 1, то ∫ δ(r→ −r→j)dV = 1.

Подставляя (11.3) в общее решение (11.2), получаем

ϕ(r→) = ∫ qδ(r→′ −r→j)dV ′ ∣r→ −r→′∣ = q ∣r→ −r→j∣ .

Следовательно, для системы точечных зарядов из интеграла (11.2) получается сумма (11.1).

Сравнивая потенциал точечного заряда ϕ = q∕r (расположенного в точке r→j = 0) с уравнением для этого потенциала Δϕ = −4π q δ(r→), получаем важное для теории математическое представление δ-функции: Δ1 r = −4πδ(r→) . (11.4)

Рис. 1.24: График функции exp(−x∕a2) πa при последовательно уменьшающихся значениях параметра a: 0,4, 0,2 и 0,1.

С физической точки зрения, распределение заряда в виде δ-функции есть объект предельно малых размеров, которыми можно пренебречь по сравнению с другими размерами задачи. При этом не исключено, что в другой задаче тот же объект нельзя будет считать малым. Существует множество представлений δ-функции, получаемых из гладких функций при предельных переходах. Например:

δ(r→) = lima→0 exp(−r2∕a2) (πa2)3∕2 .

Наряду с трехмерной δ-функцией вводят также δ-функции других размерностей. Например, одномерная δ-функция используется для описания поверхностного распределения заряда: ρ(x) = σ δ(x). (11.5)

Её также можно представить в виде предельного перехода; например:

δ(x→) = lima→0 exp(−x∕a2) πa .

Одномерная δ-функция обладает свойствами, аналогичными свойствам трехмерной δ-функции:

δ(x) = 0 всюду, кроме x = 0;

∫ f(x)δ(x)dx = f(0).

Однако аналога представления (11.4) для неё не существует. Заметим также, что

δ(r→) = δ(x)δ(y)δ(z).

Для полноты картины осталось проверить, что интеграл (11.2) действительно удовлетворяет уравнению Пуассона, т.е.

Δ ∫ V ρ(r→′)dV ′ ∣r→ −r→′∣ = −4πρ(r→).

Для этого заметим, что оператор Δ можно внести под знак интеграла, поскольку Δ подразумевает дифференцирование по координатам r→, а интегрирование производится по r→′. Далее воспользуемся соотношением (11.4) и свойствами δ-функции:

Δϕ = ∫ ρ(r→′)Δ 1 ∣r→ −r→′∣ dV ′ = ∫ ρ(r→′)[ − 4π δ(r→ −r→′)]dV ′ = −4πρ(r→).