Сравнение двоичных чисел

Сравнение многоразрядных чисел основывается на проверке равенства цифр чисел. Пусть даны два числа А3А2А1А0 и В3В2В1В0 . Сравниваются В3 и А3 , В2 и А2 , В1 и А1 , В0 и А0 , по результатам сравнения делается вывод: если совпали и третьи цифры, и вторые, и первые, и нулевые, то числа одинаковы.

Таблица истинности поразрядного сравнения изображена на рис. 22.7.

Рис. 22.7. Таблица истинности поразрядного сравнения

С помощью законов алгебры логики возможно представить выражение выходного сигнала:

, (22.2)

где .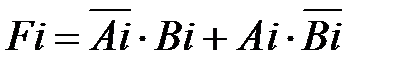

Переключательную функцию F позволяют реализовать логические двухвходовые элементы "Исключающее ИЛИ". На рис. 22.8 показан один из вариантов реализации схемы сравнения.

Рис. 22.8. Реализация схемы сравнения на ИС 155ЛП5 и 155ЛР3

Возможно построение более сложной схемы сравнения, которая определяет равенство чисел, а также, какое из чисел больше. Она может определять равенство двух двоичных чисел А и В с одинаковым количеством разрядов либо вид неравенства А > В или А < В. Цифровые компараторы имеют три выхода. Схема одноразрядного компаратора представляет собой структуру логического элемента «Исключающее ИЛИ-НЕ» (рис. 22.9).

Рис. 11.9. Цифровой компаратор с тремя выходами

Из анализа схемы следует, что если А = В, то F = 1, в противном случае, т.е. при А ≠ В, F = 0. Если А > В, т. е. А = 1, В = 0, то С = 1, а если А < В, т.е. А = 0, В = 1, то D = 1.

Если попарно равны между собой все разряды двух n-разрядных двоичных чисел, то равны и эти два числа А и В. Применяя цифровой компаратор для каждого разряда, например, четырехзначных чисел, и определяя значения F1, F2, F3, F4 логических переменных на выходах компараторов, факт равенства А = В установим в случае, когда F = F1• F2 • F3 • F4 = 1. Если же F = 0, то А ≠ В.

Неравенство А > В обеспечивается (для четырехразрядного числа) в четырех случаях: или А4 > В4, или А4 = В4 и А3 > В3, или А4 = В4, А3 = В3 и А2 > В2, или А4 = В4, А3 = В3, А2 = В2 и A1 > B1 (где А4 и В4 – старшие разряды чисел А и В). Очевидно, что если поменять местами Ai и Вi, то будет выполняться неравенство А < В.

В настоящее время промышленностью выпускаются готовые четырехразрядные схемы сравнения чисел (рис. 22.10).

Рис. 22.10. Цифровые компараторы: а) К134СП1, б) К555СП1

Представленные микросхемы являются четырехразрядными компараторами, в которых каждый из одноразрядных компараторов аналогичен рассмотренной ранее схеме. Данные микросхемы имеют расширяющие входы А < В, А = В, А >В, что позволяет наращивать разрядность обоих чисел.