ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ЖИВОГО СЕЧЕНИЯ

ПОТОКА В КАНАЛЕ

Наиболее часто встречаются поперечные сечения каналов, показанные на рис. 6-2. Приведем ниже формулы, служащие для определения величин 𝜔,χ и R.

1°. Симметричное трапецеидальное поперечное сечение (рис. 6-2, а). Здесь b - ширина канала по дну; h — глубина наполнения канала; величина m, указанная на чертеже, — коэффициент откоса:

(6-12)

где угол ψ (см. чертеж) задают не по соображениям гидравлического расчета, а учитывая устойчивость грунта откоса (если откосы канала образуются нескаль­ным грунтом). Ширина потока поверху:

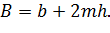(6-13)

Величины живого сечения со и смоченного периметра χудобно вычислять по следующим геометрическим зависимостям:

(6-14)

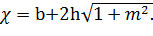(6-15)

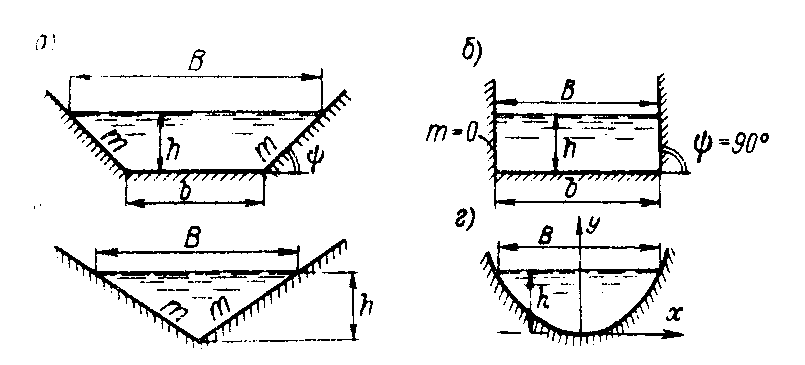
Рис. 6-2. Примеры поперечного сечения каналов

Зная 𝜔 и χ, определяем величину R:

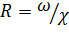(6-16)

Иногда при расчете кана­лов пользуются понятием от­носительной ширины канала по дну:

(6-17)

Величины 𝜔 и χ через β выражаются следующим обра­зом:

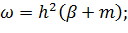(6-18)

(6-19)

2°. Прямоугольное поперечное сечение (рис. 6-2,6).Здесь

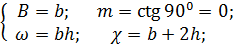(6-20)

в случае весьма широкого прямоугольного русла

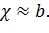(6-21)

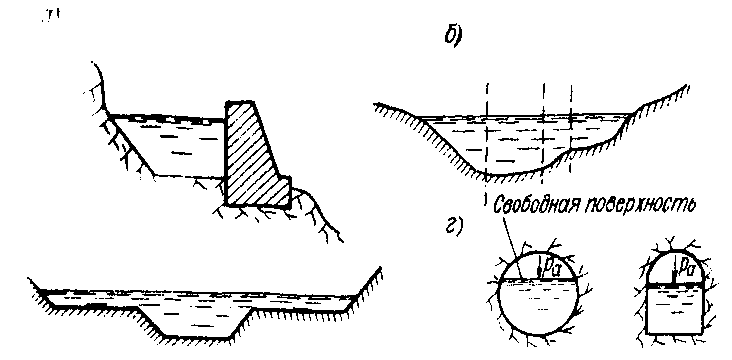
Рис. 6-3. Примеры поперечного сечения каналов

3°. Треугольное поперечное сечение (рис. 6-2, в). Здесь

(6-22)

4°. Параболическое поперечное сечение (рис. 6-2, г). Уравнение параболы, образующей смоченный периметр, имеет вид:

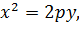(6-23)

где p-параметр параболы; оси x и yуказаны на рис. 6-2, г.Для такого русла ширина потока поверху Вможет быть найдена (для заданной глубины h) из уравнения (6-23);

(6-24)

(6-25)

5°. Прочие поперечные сечения.Отметим следующие профили:

а) несимметричный профиль (рис. 6-3, а);

б) неправильный профиль (рис. 6-3,6); в этом случае, как и в предыдущем,
величины со и х приходится вычислять, разбивая поперечное сечение канала
на отдельные части;

в) составной профиль (рис. 6-3, в);

г) замкнутые профили (рис. 6-3,г); здесь имеем так называемый закры-
тый канал.