Расчет шлицевых соединений
Как и шпонки, шлицы рассчитывается на смятие и срез:
sсм = 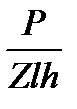 £ [s]см
£ [s]см
t = 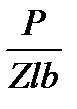 £ [t] Р =
£ [t] Р = 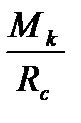
где Rc - средний радиус шлицов;
Мk - крутящий момент на оси вала.
ГЛАВА ΙΙа
Соединение деталей посадкой с натягом (прессовые соединения)
2.1. Общие сведения
Соединение двух деталей по круговой цилиндрической поверхности можно осуществить непосредственно без применения болтов, шпонок и т. д. Для этого достаточно при изготовлении деталей обеспечить натяг посадки, а при сборке запрессовать одну деталь в другую (рис.2.1)
Натягом N называют положительную разность диаметров вала и отверстия, N=B—А.
Перед запрессовкой После запрессовки
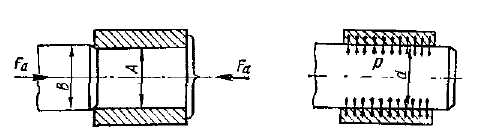
Рис. 2.1
После сборки вследствие упругих и пластических деформаций диаметр dпосадочных поверхностей становится общим. При этом на поверхности посадки возникают удельное давление ри соответствующие ему силы трения. Силы трения обеспечивают неподвижность соединения и позволяют воспринимать как крутящие, так и осевые нагрузки. Защемление вала во втулке позволяет, кроме того, нагружать соединение изгибающим моментом. В инженерной практике такое соединение называют прессовым.
Нагрузочная способность прессового соединения прежде всего зависит от натяга, значение которого устанавливают в соответствии с нагрузкой. Практически расчетный натяг очень невелик, он измеряется микрометрами и не может быть выполнен точно. Неизбежные погрешности производства приводят к рассеиванию натяга и следовательно к рассеиванию нагрузочной способности соединения. Рассеивание натяга регламентируется стандартом допусков и посадок. Изучение допусков и посадок является предметом курса «Взаимозаменяемость и технические измерения». В курсе «Детали машин» излагается расчет прочности соединения.
 Сборку любого прессового соединения выполняют одним из трех
Сборку любого прессового соединения выполняют одним из трех
способов: прессованием, нагревом втулки, охлаждением вала.
Прессование — распространенный и несложный способ сборки.
Однако этому способу свойственны недостатки; смятие и
частичное срезание (шабровка) шероховатостей посадочных
поверхностей, возможность неравномерных деформаций
деталей и повреждения их торцов. Шабровка и смятие
шероховатостей приводят к ослаблению прочности соединения
до полутора раз по сравнению со сборкой нагревом или
| Рис. 2.2 |
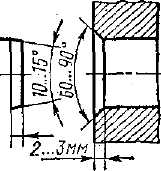
охлаждением. Для облегчения сборки и уменьшения шабровки концу вала и краю отверстия рекомендуют придавать коническую форму (рис. 2.2).
Шабровка поверхностей контакта устраняется полностью при сборке по методу нагревания втулки (до 2ОО...400°С) или охлаждения вала (твердая углекислота -79C0 , жидкий воздух— 196°С). Недостатком метода нагревания является возможность изменения структуры металла, появление окалины и коробления. Метод охлаждения свободен от этих недостатков.
Необходимую разность температур tнагрева втулки или охлаждения вала, обеспечивающую свободную сборку, подсчитывают по формуле
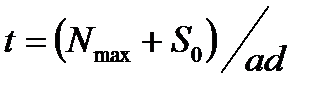 ,
,
где Nmax — наибольший натяг посадки; So — минимально необходимый зазор, обеспечивающий свободную сборку (рекомендуется принимать равным минимальному зазору посадки H7/g6); a — температурный коэффициент линейного расширения (для стали и чугуна 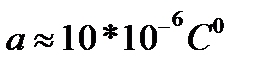 ; d — номинальный диаметр посадки.
; d — номинальный диаметр посадки.
2.2. Прочность соединения
Как было указано в разделе 2.1, стандартную посадку выбирают по условиям неподвижности соединения при заданной нагрузке без каких-либо дополнительных скреплений. Однако возможны случаи, когда назначенная посадка недопустима по условиям прочности сопрягаемых деталей, т. к. её натяг вызывает их разрушение или чрезмерные деформации. Поэтому при расчёте прочности прессовых посадок необходимо рассматривать как условия прочности (неподвижности) соединения, так и условия прочности деталей.
Расчет прочности деталей является проверкой возможности применения намеченной посадки.
 Расчет прочности соединения.
Расчет прочности соединения.
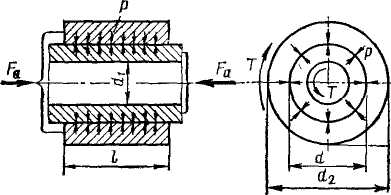
На рис.2.3 приведена расчетная схема прессового соединения. Условие прочности соединения при нагружении осевой силой KFa<,fpndl, (2.2), где
р— давление на поверхность контакта; К — коэффициент запаса = 1,5...2 .
| Рис. 2.3 |
Условие прочности соединения при погружении крутящим моментом
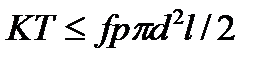 . (2.3)
. (2.3)
При совместном действии Т и Fa 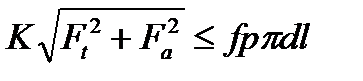 , (2.4)
, (2.4)
где Ft=2T/d — окружная сила.
По теории расчета толстостенных цилиндров, изучаемой в курсе сопротивления материалов, удельное давление на поверхности контакта связано с натягом зависимостью
p = 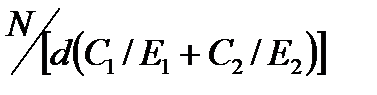 , (2.5)
, (2.5)
где N — расчетный натяг; С1 и С2 — коэффициенты:
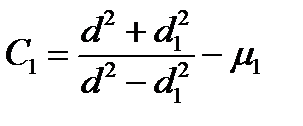 ;
; 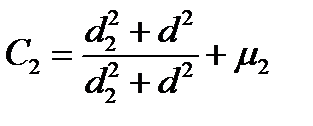 ,
,
Ei и Е2, μ1 и μ2 — модули упругости и коэффициенты Пуассона материалов вала и втулки:
для стали Е = (21...22)*104 МПа и μ = 0,3,
для чугуна Е =(12...14)*104 МПа и μ = О,25,
для бронзы Е = (10...11)*104 МПа и μ = 0,33.
При расчете прочности соединения расчетный натяг N определяют по минимальному табличному или вероятностному натягу с поправкой ина срезание и сглаживание шероховатости поверхности при запрессовке (если сборку выполняют нагреванием или охлаждением, и =0):
N = Nmin –u , u = 1.2(Rz1 + Rz2 ),
Где Rz1 и Rz2 — высоты шероховатостей посадочных поверхностей.
Наиболее распространенные значения Rz для поверхностей прессовых соединений: 10...6,3; 3,2...1,6 мкм, что соответствует 6...8-му классам шероховатости.
Экспериментальные исследования показали, что значение коэффициентов трения на контактной поверхности зависит от многих факторов: способа сборки, удельного давления р, шероховатости поверхности, рода смазки поверхностей, применяемой при запрессовке деталей, скорости запрессовки и пр. Поэтому точное значение коэффициента трения может быть определено только испытаниями при заданных конкретных условиях. В приближенных расчетах прочности соединения стальных и чугунных деталей принимают: 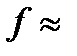 0,08...0,1 — сборка прессованием;
0,08...0,1 — сборка прессованием;  О,12. ..0,14 — сборка с нагревом или охлаждением.
О,12. ..0,14 — сборка с нагревом или охлаждением.
Изгибающий момент, которым может быть нагружено соединение, определяют на основе следующих расчетов (рис. 2.4). Действие момента (M=FL) вызывает в соединении такое перераспределение давления р, при котором внешняя нагрузка уравновешивается моментом внутренних сил MR=Rx.
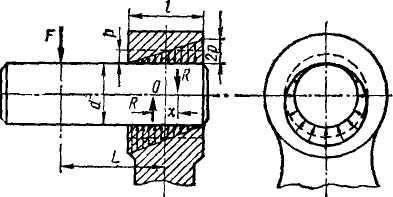 Составляя расчетные зависимости, полагают, что поворот шипа происходит вокруг центра тяжести соединения — точки О, а первоначальная равномерная эпюра давлений (на чертеже показана штриховой линией) переходит в треугольную, как показано на рис. 2/4, или трапецеидальную. Кроме того, не учитывают действие силы F, перенесенной в точку О, как малое в сравнении с действием момента М. Максимально давление изменяется в плоскости действия нагрузки. При некотором значении нагрузки эпюра давления из трапеции превращается в треугольник с вершиной у края отверстия и основанием, равным 2р. Этот случай является предельным, так как дальнейшее увеличение нагрузки приводит к появлению зазора (раскрытие стыка). Учитывая принятые положения, можно написать: M = FL = Rx,
Составляя расчетные зависимости, полагают, что поворот шипа происходит вокруг центра тяжести соединения — точки О, а первоначальная равномерная эпюра давлений (на чертеже показана штриховой линией) переходит в треугольную, как показано на рис. 2/4, или трапецеидальную. Кроме того, не учитывают действие силы F, перенесенной в точку О, как малое в сравнении с действием момента М. Максимально давление изменяется в плоскости действия нагрузки. При некотором значении нагрузки эпюра давления из трапеции превращается в треугольник с вершиной у края отверстия и основанием, равным 2р. Этот случай является предельным, так как дальнейшее увеличение нагрузки приводит к появлению зазора (раскрытие стыка). Учитывая принятые положения, можно написать: M = FL = Rx,
где R — равнодействующая давлений на поверхностях верхнего и нижнего полуцилиндров. Значение этой равнодействующей определяется давлением р прессовой посадки и не изменяется от действия изгибающего момента
R = pld.
| Рис. 2.4 |
Плечо пары х=l /3. Подставляя, получаем M = pdl2 /3
Для обеспечения необходимого запаса прочности соединения на практике принимают
M<0,2pdl2. (2.7)
При этом давление в наиболее нагруженных точках соединения не должно вызывать пластических деформаций.
Изменение давлений, вызванное действием изгибающего момента, не отражается на способности соединения воспринимать осевую силу и крутящий момент, так как суммарное значение сил трения остается постоянным.

Расчет прочности и деформаций деталей прессового соединения
выполняют по формулам для толстостенных цилиндров. Эпюры
напряжений в деталях 1 и 2 показаны на рис. 2.5, где σr — на-
пряжения сжатия в радиальном направлении; σt1 и σt2 — на-
пряжения сжатия и растяжения в тангенциальном направлении
(осевые напряжения малы, их не учитывают). Давление рпри
расчете прочности деталей определяют [см. формулу (2.5)] по
максимальному натягу
N = Nmax — u. (2.8)
Приведенные зависимости справедливы только в пределах
| Рис. 2.5 |
дет пластических деформаций (по теории наибольших ка-
сательных напряжений): σэк =σ1 – σ3 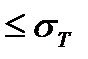 ,
,
где σ1—максимальное, а σ3—минимальное нормальные напряжения, считая растяжение положительным; σТ—предел текучести материала.
Нетрудно установить, что наибольшие эквивалентные напряжения σэк имеют место в точках внутренних поверхностей втулки и вала. При этом для втулки σ1= σt2; σt3 = - σr = -р
и условия отсутствия пластических деформаций
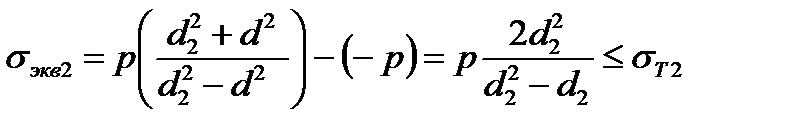 ,
,
или 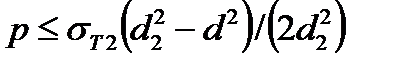 (2.9)
(2.9)
где σт2—предел текучести материала втулки; для вала σ1 == 0 , σ3 =- σt1 и σэкв1 = σt1 или 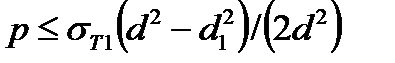 (2.10)
(2.10)
Появление пластических деформаций не является во всех случаях недопустимым. Опыт применения прессовых посадок свидетельствует о том, что надежные соединения могут быть получены и при наличии некоторой кольцевой пластической зоны вблизи внутренней поверхности втулки. Давление на поверхности контакта при наличии пластических деформаций можно определять по приближенным формулам:
при 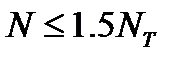 p = pT (2NT – N/NT) (2.11)
p = pT (2NT – N/NT) (2.11)
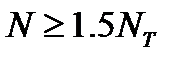 ;p=0.5pT.
;p=0.5pT.
где NT и рТ —расчетный натяг и давление, соответствующие пределу текучести.
Давление рТ определяют как меньшее из двух значений при знаке равенства в формулах (2.9) и (2.10). При известном рТ по формуле (2.5) определяют NT.
Увеличение наружного диаметра втулки, вызванное растяжением от посадки, можно оценить по формуле 
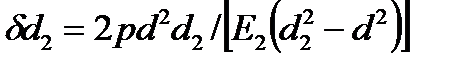 (2.12)
(2.12) 

|
| Рис. 2.6 |
| Рис. 2.7 |
Дата добавления: 2015-11-28; просмотров: 1530;
