Лекция 2. СТРУКТУРНЫЙ СИНТЕЗ МЕХАНИЗМОВ

Число степеней свободы механизма.Шесть степеней свободы твер­дого тела, свободно движущегося в пространстве, можно рассматри­вать также как шесть независимых координат, определяющих его по­ложение (например, три координаты начала подвижной системы коор­динат, связанной с телом, и три угла Эйлера, определяющие располо­жение осей подвижной системы координат относительно неподвижной).

Их принято называть обобщенными, так как они определяют положе­ние всего твердого тела. Аналогично, обобщенными координатами ме­ханизма называют независимые между собой координаты, определяю­щие положения всех звеньев механизма относительно стойки. Число обобщенных координат механизма равно числу степеней свободы меха­низма, если все связи в кинематических парах — геометрические, т. е. налагают ограничения только на положения (координаты) точек звеньев.

Общее число координат, определяющих положение п подвижных звеньев механизма, равно 6д. Каждая кинематическая пара класса т.

дает т уравнений связи, в которые входят координаты звеньев. Общее число этих уравнений равно

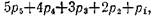
где р₅ — число пар пятого класса, р₄ — число пар четвертого класса, и т. д.

Если все уравнения связи независимы, т. е. ни одно из них не мо­жет быть получено как следствие других, то разность между общим числом координат и числом уравнений, связывающих эти координаты, дает число независимых координат (число степеней свободы меха­низма)

Для плоского механизма, т. е. механизма, все подвижные звенья которого совершают плоское движение, параллельное одной и той же неподвижной плоскости, формула (2.1) принимает вид

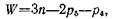
так как в плоском движении положение твердого тела определяется тремя координатами и соответственно кинематические пары могут быть только одноподвижными (пятого класса) и двухподвижными (чет­вертого класса). Для этих пар сохранены обозначения с индексами классов пар, хотя в плоских механизмах относительная подвижность пары не связана однозначно с ее классом. Например, сферическая пара (третьего класса) в плоском механизме кинематически эквивалентна вращательной паре, цилиндрическая пара (четвертого класса) также эквивалентна вращательной, если ось цилиндра перпендикулярна плоскости движения. Кроме того, заметим, что в плоских механизмах одноподвижные пары обычно являются низшими, а двухподвижные — высшими. Расположение кинематических пар должно обеспечивать всем звеньям плоское движение, параллельное одной и той же непо­движной плоскости. Например, в механизме с одними вращательными парами, который называется шарнирным, оси всех пар должны быть параллельны между собой.

Структурный синтез механизмов. Структурным синтезом механиз­ма называется проектирование структурной схемы механизма, под которой понимается схема механизма, указывающая стойку, подвижные звенья, виды кинематических пар и их взаимное расположение. Струк­турная схема может быть представлена или графически с применением условных обозначений звеньев и кинематических пар, или же анали­тической записью, допускающей применение ЭВМ.

Для механизмов, в состав которых входят только незамкнутые кинематические цепи, возможные варианты их структурных схем на­ходятся при заданном числе степеней свободы непосредственно по формуле (2.1). В механизмах с незамкнутыми кинематическими цепя­ми число подвижных звеньев равно числу кинематических пар и фор­мула (2.1) принимает вид

т. е. число степеней свободы механизма равно сумме подвижностей кинематических пар.

В табл. 3 приведены некоторые структурные схемы механизмов манипуляторов. Звенья механизма обозначены арабскими цифрами.

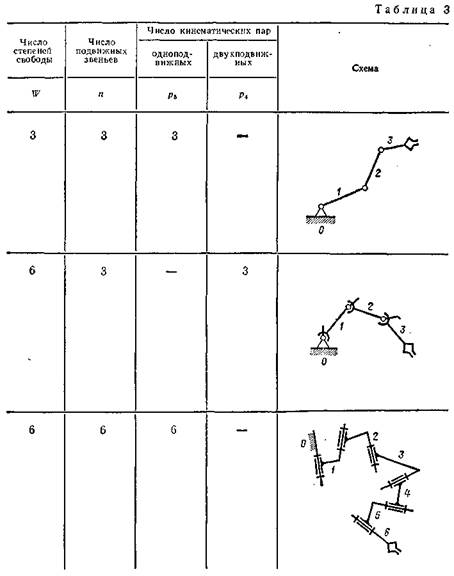
Элементы кинематических пар, принадлежащие стойке, отмечены под-штриховкой оси или треугольниками с подштриховкой. На последнем звене механизма, которое входит только в одну кинематическую пару, условно показан захват (по другой терминологии — схват), т. е. уст­ройство, позволяющее подобно пальцам человека захватывать пере­мещаемый предмет. Кинематические пары с числом степеней свободы

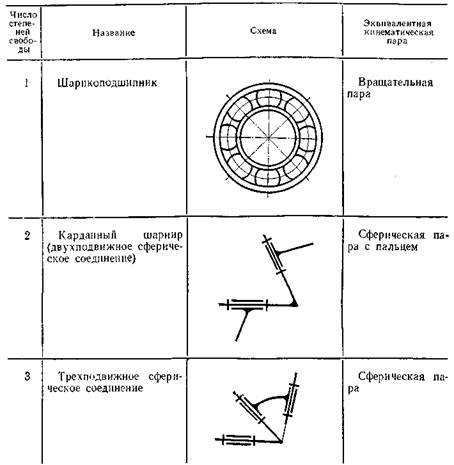
более двух применяются здесь редко. Сферическая пара с пальцем обычно выполняется в виде карданного шарнира (см. табл. 2).

Для механизмов, в состав которых входят замкнутые кинематиче­ские цепи, вначале устанавливают возможные варианты этих цепей, а затем из каждой кинематической цепи получают несколько различных механизмов, принимая поочередно за стопку различные звенья цепи. Например, для плоских шарнирных механизмов с одной степенью сво­боды по формуле (2.2)

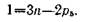
Наименьшее целое число /г>1, при котором удовлетворяется это урав­нение, равно трем (р₆=4), т. е. механизм должен иметь четыре звена (считая и стойку),которые последо­вательно соединяются вращатель­ными парами, образуя замкнутую кинематическую цепь. На рис. 2

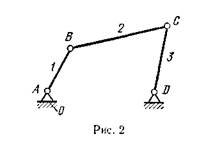
показана структурная схема механизма, называемого шарнирным че-тырехзвенником, который образуется из кинематической цепи ABCD, если за стойку принять звено AD. Из той же кинематической цепи мож­но образовать еще три механизма, принимая за .стойку какое-либо дру­гое звено (АВ, или ВС, или CD).

Для пространственного механизма, в котором все звенья образуют только вращательные пары с осями, расположенными как угодно в пространстве, по формуле (2.1)

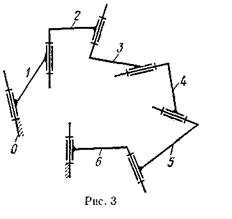
Это уравнение в целых числах удовлетворяется при п=6 и р₅=7, т. е. механизм должен иметь 7 звеньев (считая и стойку), которые по­следовательно соединяются между собой при помощи вращательных пар, образуя замкнутую семизвенную кинематическую цепь. Получен­ный механизм называется пространственным шарнирным семизвенником. Его структурная схема показана на рис. 3.

Число звеньев в пространственных механизмах можно уменьшить, если кроме одноподвижных пар применять пары с большей подвиж­ностью. Пусть, например, для механизма с одной степенью свободы п=2. По формуле (2.1),

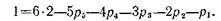
Это уравнение в целых числах удовлетворяется при следующих сочетаниях:

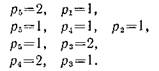
Полученные сочетания определяют только числа кинематических пар различной подвижности. Для получения всех возможных кинема­тических цепей, удовлетворяющих поставленным условиям, надо еще указать варианты, отличающиеся последовательностью расположения кинематических пар. Например, две одноподвижные пары могут быть смежными и несмежными. Кроме того, одноподвижная пара может быть вращательной, поступательной, винтовой; двухподвижная пара может быть цилиндрической, сферической с пальцем и т. д. Поэтому общее число вариантов замкнутых кинематических цепей, а следова­тельно и механизмов, получается достаточно большим.

Начальные звенья. За обобщенные координаты механизма можно взять любые переменные координаты, определяющие положения одно­го или нескольких звеньев механизма. Звено, которому приписывается одна или несколько обобщенных координат механизма, называется на­чальным звеном. Происхождение этого термина связано с тем, что опре­деление положений всех звеньев механизма начинается с определения положений начальных звеньев.

В механизме с одной степенью свободы — одно начальное звено и за обобщенную координату обычно принимается или угловая коорди­ната вращающегося звена, или линейная координата прямолинейно движущегося звена. Начальное звено не обязательно совпадает с вход­ным звеном. Можно за начальное звено взять выходное звено или даже промежуточное, если при этом упрощается анализ механизма. В меха­низмах с двумя степенями свободы могут быть или два начальных зве­на, если за обобщенные координаты приняты координаты двух раз­личных звеньев, или одно начальное звено, если оно образует со стой­кой двухподвижную пару.

Образование плоских и пространственных механизмов путем на­слоения структурных групп (групп Ассура). Для структурного синтеза многозвенных механизмов с числом звеньев более четырех непосредст­венный перебор всех возможных вариантов по формулам (2.1) и (2.2) оказывается затруднительным. В этом случае более удобно находить структурные схемы механизмов путем последовательного наслоения некоторых кинематических цепей, называемых структурными груп­пами или группами Ассура¹. Принцип этого наслоения покажем на примере образования плоского шестизвенного шарнирного механизма.

В механизме с одной степенью свободы положения всех звеньев определяются заданием одной обобщенной координаты, или, что то же, положением одного начального звена. На рис. 4, а показано начальное звено 1, которое входит во вращательную пару со стойкой 0. Число степеней свободы этого звена относительно стойки W—1 (одна обоб­щенная координата cpi). Механизм в целом тоже должен иметь W=\. Поэтому мы можем присоединять (наслаивать) только такие кинема­тические цепи, которые удовлетворяют условию W=0. В нашем слу­чае согласно формуле (2.2) это условие имеет вид

Зга—2р₅=0. (2.4)

Простейшая кинематиче­ская цепь, удовлетворяющая

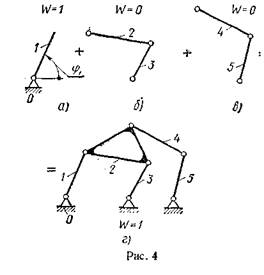
условию (2.4) при п=2 и р₅=3, называется двухповодковой группой (рис. 4,6). В ней одна из вращательных пар (внутренняя) образуется звеньями группы, а другие две (внешние) образуются после присоединения звеньев группы к каким-либо двум звеньям механизма. В нашем при­мере присоединение двухповодковой группы одной внешней парой к начальному звену, а другой — к стойке не изменяет числа степеней свободы, которое остается равным 1. Далее можно присоединить к зве­ну 2 и к стойке 0 вторую двухповодковую группу, состоящую из звень­ев 4 и 5 (рис. 4, в). В результате получим шестизвенный шарнирный механизм с W—\ (рис. 4, г). Вторую группу из звеньев 4 и 5 можно присоединять также к звеньям 2 и 3. Тогда получится другой тип ше-стизвенного шарнирного механизма (рис. 5).

Теперь можно дать общее определение термина «структурная груп­па». Структурной группой называется кинематическая цепь, число степеней свободы которой равно нулю относительно элементов ее внеш­них пар, причем группа не должна распадаться на более простые ки­нематические цепи, удовлетворяющие этому условию. Например, кине­матические цепи, состоящие из звеньев 2, 3, 4 и 5 (см. рис. 4 и 5), рас­падаются на две двухповодковые группы.

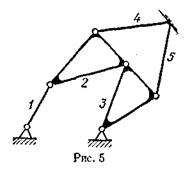
В табл. 4 показаны некоторые плоские структурные группы, со­стоящие из звеньев, входящих во вращательные пары. По предложе­нию И. И. Артоболевского ¹ номер класса группы равен числу кинематических пар, входящих в замкнутый контур, образованный внутренними кинематическими парами.

Принцип наслоения структурных групп распространяется на все виды механизмов, составленных только из твердых тел. Для плоских механизмов с одно- и двухподвижными парами структурные группы удовлетворяют условию

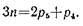
Структурные группы пространственных механизмов удовлетворяют аналогичному условию

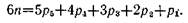
Как плоские, так и пространственные структурные группы ис­пользуются не только при структурном синтезе, но и при анализе ме­ханизмов.

Избыточные связи. При выводе формулы (2.1) предполагалось, что все уравнения связи независимы. В некоторых механизмах это условие не выполняется. Тогда разность между общим числом уравне­ний связи и числом независимых уравнений связи называется числом избыточных связей, а механизм, в котором общее число уравнений связи

больше числа независимых уравнений связи, называется механизмом с избыточными связями.

Обозначая число избыточных связей через q, получаем, что число независимых уравнений связи равно

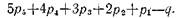
Следовательно, число независимых координат (число степеней свободы механизма)

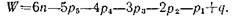
Уравнение (2.7) содержит две неизвестные величины (W и q), так как число избыточных связей в общем случае можно определить лишь путем анализа уравнений связи. Однако в некоторых простейших случаях величина W может быть получена путем непосредственного решения задачи о положениях звеньев механизма. Тогда из уравнения (2.7) находим число избыточных связей:

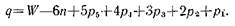
Избыточные связи получаются обычно при конструировании плос­ких механизмов. Например, в плоском шарнирном четырехзвеннике (см. рис. 2) W—\ и по формуле (2.8) получаем q~\—6-3+5-4=3, т. е. в этом механизме есть три избыточные связи. Избыточными они назы­ваются потому, что их можно устранить, сохраняя заданное число сте­пеней свободы W (в нашем примере W=l). Устранение избыточных связей выполняется изменением подвижностей отдельных кинемати­ческих пар, причем для одного и того же механизма с избыточными свя­зями можно найти несколько вариантов механизмов без избыточных связей. Например, в шарнирном четырехзвеннике можно любые две вращательные пары заменить: одну на сферическую, а другую на сфе­рическую с пальцем (первый вариант), или одну на сферическую, а другую на цилиндрическую (второй вариант). Легко проверить по формуле (2.8), что в обоих вариантах механизмов отсутствуют избыточ­ные связи.

Возможны и другие варианты устранения избыточных связей в шарнирном четырехзвеннике. Следовательно, в этом механизме, как и в любом другом механизме с избыточными связями, нельзя указать, какая именно связь является избыточной. Можно лишь определить число этих связей и затем в зависимости от конструктивных условий соответственно уменьшить общее число связей.

Наличие избыточных связей в механизмах ответственного назначе­ния требует повышенной точности изготовления элементов кинемати­ческих пар во избежание дополнительных нагрузок на звенья меха­низма из-за их деформации. Например, если в шарнирном четырех­звеннике непараллельность осей вращательных пар не может быть компенсирована зазорами между элементами этих пар, то его надо рассматривать как пространственный механизм с произвольным рас­положением осей вращательных пар. Число степеней свободы опреде­ляется в этом случае по формуле (2.1):

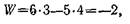
т. е. получается не механизм, л ферма (.дважды статически неопредели­мая), и его звенья могут двигаться только за счет деформаций. Эти деформации вызывают дополнительные нагрузки на звенья и увеличе­ние сил трения в кинематических парах. Если же устранить избыточ­ные связи, то можно снизить точность изготовления-при одновремен­ном уменьшении дополнительных нагрузок на звенья механизма ¹. Необходимо только проверять жесткость всей конструкции, с тем чтобы не возникли дополнительные нагрузки от вредных коле­баний.

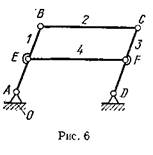
Иногда избыточные связи умышленно вводят в состав механизма для повышения его жесткости или для устранения неопреде­ленности движения звеньев в некоторых по­ложениях. Эти избыточные связи существу­ют при выполнении определенных геометри­ческих соотношений в механизме. Например, в механизме сдвоенного параллелограмма (рис. 6) имеются соотношения AB = CD, BC=AD (т. е. фигура ABCD — параллелограмм) и AE=FD, EF=AD (т. е. фигура AEFD — тоже параллелограмм). По свойству параллелограмма расстояние между точками Е и F всегда равно отрезку AD, если эти точки находятся на равных расстояниях от точек А и D. Поэтому введение дополнитель­ного звена 4 при условии, что EF=AD, не вносит новых геометриче­ских связей и число степеней свободы остается равным 1, хотя по формуле (2.2) Г=3-4—2-6=0.

Если точность выполнения указанных геометрических соотношений окажется недостаточной, например AE^FD, то расстояние EF уже не будет равно AD и движение станет невозможным, т. е. число степе­ней свободы действительно будет равно нулю.

В заключение еще раз подчеркнем, что формулы (2.1) и (2.2) пред­назначены в основном не для определения числа степеней свободы, а для структурного синтеза механизмов без избыточных связей.