Виды степенных средних величин. 7.2.1. Средняя арифметическая(k = 1)
7.2.1. Средняя арифметическая(k = 1)
Средняя арифметическая наиболее распространенный вид средних величин. В зависимости от характера имеющихся данных, как и все степенные средние, может быть простой или взвешенной.
Средняя арифметическая простая рассчитывается для несгруппированных данных, представляющих собой n значений признака x:
.
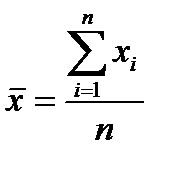Пример. Определить по имеющимся данным (табл. 7.1) среднюю заработную плату работника.
Таблица 7.1 – Заработная плата работников
| ФИО работника | Заработная плата, тыс. руб. |
| Иванов И.И. Петров В.С. Сидоров П.Г. | |
| Итого |
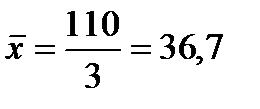тыс. руб.
Таким образом, средняя заработная плата составляет 36,7 тыс.руб.
Средняя арифметическая взвешенная рассчитывается по сгруппированным данным: дискретным и интервальным вариационным рядам:
.
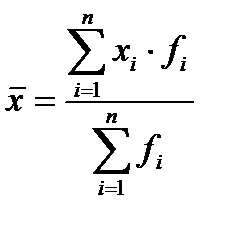Веса (fi) могут быть представлены абсолютными, но и относительными величинами (в процентах или долях единицы).
Пример. Определить по имеющимся данным (табл. 7.2) среднюю заработную плату работника.
Таблица 7.2 – Заработная плата работников
| Заработная плата, тыс. руб. | Число работников, чел. |
| Итого |
Чтобы по данному дискретному вариационному ряду получить фонд заработной платы, необходимо заработную плату (xi) умножить на число работников (fi) и полученные произведения сложить. Для выполнения расчетов введем дополнительный столбец (xi·fi):
| Заработная плата, тыс. руб. | Число работников, чел. | xi·fi |
| 30·2 = 60 38·5 = 190 42·3 = 126 | ||
| Итого |
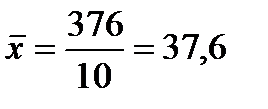тыс. руб.
Таким образом, средняя заработная плата составляет 37,6 тыс.руб.
Пример. Определить по имеющимся данным (табл. 7.3) среднюю заработную плату работника.
Таблица 7.3 – Заработная плата работников
| Заработная плата, тыс. руб. | Число работников, чел. |
| 30 – 35 35 – 40 40 – 45 | |
| Итого |
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам. При этом величины открытых интервалов (первого и последнего) условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего).
В нашем примере интервалы закрытые. Для решения задачи введем необходимые расчетные столбцы (середина интервала, xi·fi ):
| Заработная плата, тыс. руб. | Число работников, чел. | Середина интервала | xi·fi |
| 30 – 35 35 – 40 40 – 45 | 32,5 37,5 42,5 | 32,5·2 = 65,0 37,5·5 = 187,5 42,5·3 = 127,5 | |
| Итого | х |
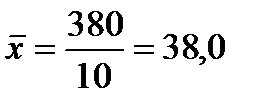тыс. руб.
Таким образом, средняя заработная плата составляет 38,0 тыс.руб.
Дата добавления: 2015-12-26; просмотров: 381;