Сущность средних величин

Статистика изучает варьирующие признаки, т.е. индивидуальные значения одного и того же признака у различных единиц совокупности неодинаковы. Чтобы вскрыть общее, существенное, характерное для всех единиц совокупности, чтобы охарактеризовать всю совокупность в целом, нужно вычислить обобщающие показатели, представляющие собой статистическое выражение закона больших чисел, действие которого заключается во взаимопогашении случайностей и выявлении при достаточно большом числе наблюдений закономерности данного массового явления.

Средняя величина - это обобщенная количественная характеристика признака в расчете на единицу статистической совокупности. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.

Средние величины получили широкое применение в экономическом анализе. Большое аналитическое значение имеет исчисление средней производительности труда, средней заработной платы, среднегодовых темпов изменения уровня показателей во времени, среднедушевых показателей и т.д.

Теория и практика выработала ряд требований, которые предъявляются к расчету среднего показателя:

1) качественно однородная совокупность

Метод средних используется в сочетании с методом группировок: если совокупность неоднородна - общие средние должны быть заменены или дополнены групповыми средними, т.е. средними, рассчитанными по качественно однородным группам.

2) массовость данных

Только при достаточно большом числе единиц совокупности взаимопогашаются возможные случайные отклонения и средняя величина правильно характеризует типичный размер изучаемого признака.

Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:

.

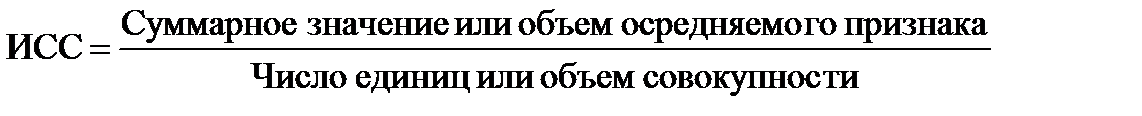Например,

;

;

.

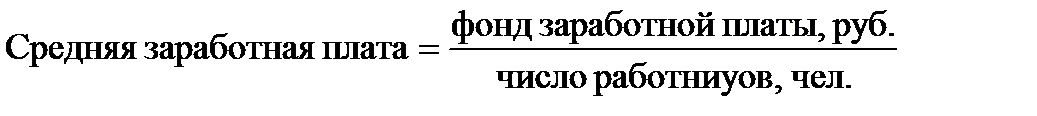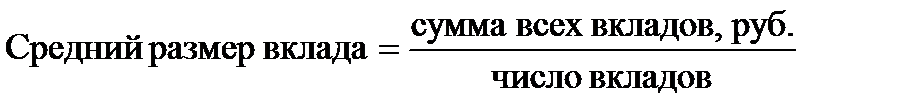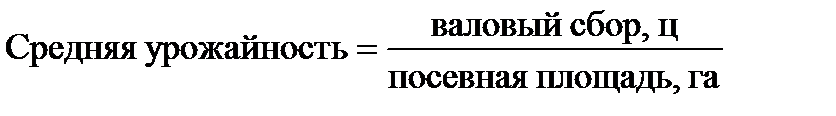Для каждого показателя, используемого в социально-экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней. Выбор вида средней величины зависит от:

- цели исследования;

- экономической сущности осредняемого показателя;

- имеющихся исходных данных.

Основополагающее правило при этом заключается в том, что величины, являющиеся числителем и знаменателем средней, должны иметь определенный логический смысл. В каждом конкретном случае для реализации исходного соотношения потребуется одна из следующих форм средней величины:

- средняя арифметическая;

- средняя гармоническая;

- средняя геометрическая;

- средняя квадратическая, кубическая и т.д.

Перечисленные средние объединяются в общей формуле средней степенной:

; ,

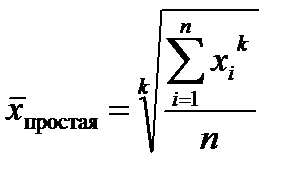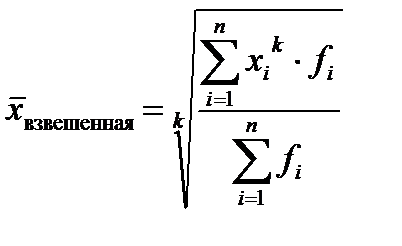где 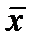- степенная средняя;

k - показатель степени средней;

x_i – варианта, индивидуальное значение признака;

n – число вариант;

f_i – вес, частота, число единиц совокупности с данным значением признака

Помимо степенных средних в статистике также используются структурные средние, среди которых наиболее распространенными являются мода и медиана.