Свойства средней арифметической
Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчетах.
1. Произведение средней на сумму частот всегда равно сумме произведений отдельных вариантов на соответствующие им частоты:
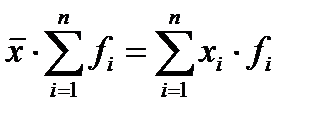 .
.
2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:
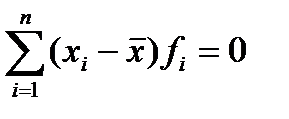 .
.
3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:
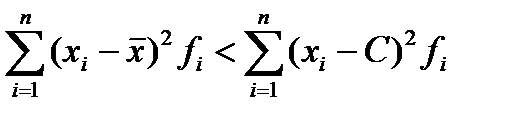 .
.
4. Если от каждой варианты вычесть или прибавить какое-либо произвольное постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число:
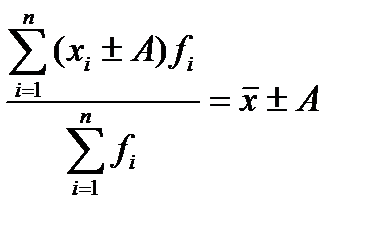 .
.
5. Если каждую варианту разделить или умножить на какое-либо произвольное постоянное число h, то и средняя также соответственно уменьшится или увеличится в h раз:
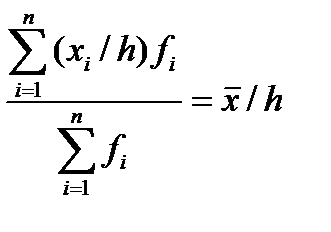 ;
; 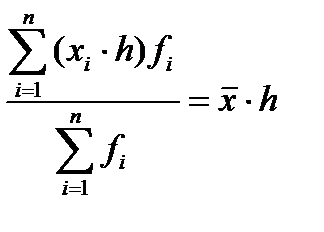 .
.
6. Если все частоты разделить или умножить на какое-либо число A, то средняя не изменится.
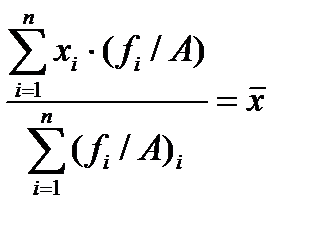 ,
, 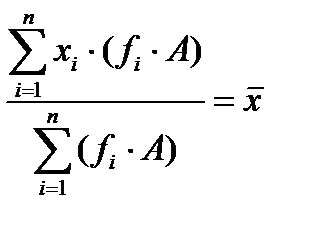 .
.
Исходя из данного свойства можно заключить, что в случае равенства всех весов между собой расчеты по средней арифметической взвешенной и средней арифметической простой приведут к одному и тому же результату.
7.2.2. Средняя гармоническая(k = -1)
Средняя гармоническая простая – средняя величина из обратных значений признаков:
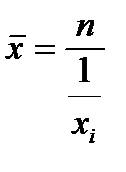 .
.
Эта форма средней величины в социально-экономических исследованиях практически не используется.
Средняя гармоническая взвешенная применяется в тех случаях, когда известны значения признака, а веса в явном виде не представлены:
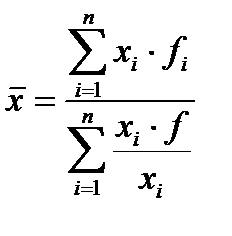 или
или 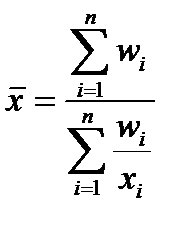 ,
,
где wi = xi·fi ,
Пример. Определить по имеющимся данным (табл. 7.4) среднюю заработную плату работника.
Таблица 7.4 – Заработная плата работников
| Заработная плата работника в отдел, тыс. руб. | Фонд заработной платы по отделам, тыс. руб. |
| Итого |
Чтобы получить число работников (fi), необходимо фонд заработной платы (xi·fi) разделить на заработную плату (xi). Для выполнения расчетов введем дополнительный столбец:
| Заработная плата работника в отдел, тыс. руб. | Фонд заработной платы по отделам, тыс. руб. | Число работников, чел. |
| 60/30 = 2 190/38 = 5 126/42 = 3 | ||
| Итого |
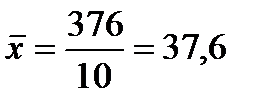 тыс. руб.
тыс. руб.
Таким образом, средняя заработная плата составляет 37,6 тыс.руб.
7.2.3. Средняя геометрическая (k = 0)
Средняя геометрическая простая:
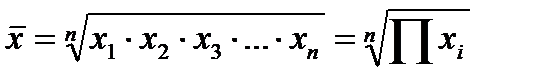 .
.
Средняя геометрическая взвешенная:
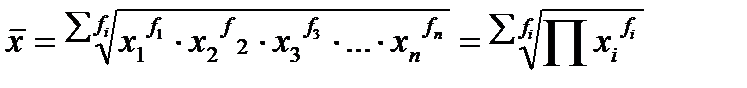 .
.
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.
7.2.4. Средняя квадратическая (k = 2)
Средняя квадратическая простая:
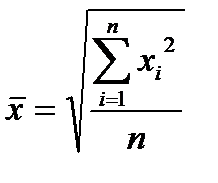 .
.
Средняя квадратическая взвешенная:
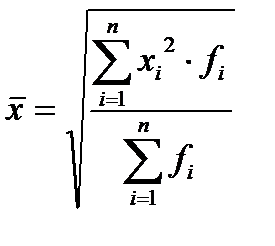 .
.
Наиболее широко этот вид средней используется при расчете показателей вариации.
В статистической практике также находят применение степенные средние 3-го и более высоких порядков.
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени (k) увеличивается и соответствующая средняя величина:
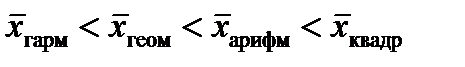 .
.
Дата добавления: 2015-12-26; просмотров: 686;
