Задачи управления горным давлением и основные принципы обеспечения устойчивости горных выработок.

Под управлением горным давлением, или, другими словами, управлением состоянием приконтурного массива пород обычно понимают совокупность мероприятий по регулированию напряжённо-деформированного состояния горных пород, окружающих горные выработки, в целях обеспечения их безопасной эксплуатации и создания необходимых условий ведения технологических процессов добычи полезных ископаемых.

Задачи управления горным давлением в капитальных и подготовительных выработках включают в себя:

а) обеспечение необходимых требований к форме, размерам поперечных сечений и сохранности выработок во времени с точки зрения обеспечения нормальных условий для выполнения технологических операций при добыче полезных ископаемых;

б) обеспечение безопасных условий работы людей и механизмов на протяжении всего срока эксплуатации выработок;

в) выбор наиболее экономичных мероприятий по обеспечению устойчивости выработок и их поддержанию.

Поскольку виды проявлений горного давления в капитальных и подготовительных выработках определяются соотношением величин действующих напряжений и деформационных характеристик окружающего массива пород, мероприятия по управлению горным давлением могут быть направлены:

* на снижение действующих напряжений в массиве;

* на повышение деформационной способности и прочностных характеристик приконтурной части массива.

По первому направлению - снижение величин действующих напряжений можно достигать следующими способами:

1. Исключать или по мере возможности снижать опасность возникновения высоких концентраций напряжений в приконтурных областях массива.

Этого можно достичь специальной организацией и методами проведения проходческих работ.

2. Придавать выработкам наиболее устойчивые формы поперечных сечений, которые определяются как видом и параметрами напряженного состояния массива пород, так и его структурными особенностями.

3. Выбирать оптимальную ориентацию сечений вертикальных выработок или направлений горизонтальных выработок в пространстве конкретного массива пород.

Второе направление - повышение деформационной способности и прочностных характеристик приконтурной части массива можно реализовать различными способами:

1. Путём искусственного упрочнения пород вокруг выработок.

К подобным мероприятиям относится тампонирование пород, в частности цементация и укрепление трещиноватых массивов битумизацией или глинизацией пород. Эти способы позволяют повысить сцепление пород в массиве.

В некоторых случаях бывает достаточно повысить прочность вмещающих пород лишь на сравнительно короткий период времени, до возведения постоянной крепи. С этой целью используют специальные способы проведения выработок с замораживанием пород.

Эффективны также кессонные способы проходки выработок при создании избыточного давления воздуха в призабойной зоне. В этом случае породы приконтурного массива постоянно находятся в условиях объёмного напряжённого состояния, а это резко изменяет в сторону увеличения их прочностные и деформационные свойства.

2. Путём применения мероприятий, направленных на максимальное использование несущей способности пород.

К ним относятся способы проходки выработок, обеспечивающие минимальное разрушение пород вокруг выработок, в частности, ведение взрывных работ методом контурного взрывания, проведение выработок бурением на полное сечение и др.

3. Путём предотвращения изменения свойств пород приконтурного массива под влиянием агентов выветривания.

Для этого в выработках применяют изолирующие виды крепи.

4. Возведение в выработках того или иного вида несущих крепей.

В рамках данной темы по первому направлению детально рассмотрим вопросы выбора устойчивых форм поперечных сечений и их ориентации в пространстве, а по второму – наиболее широко применяемые методы крепления выработок и ,частично, методы укрепления приконтурного массива.

Закономерности изменения напряженного состояния приконтурного массива выработок при их различных положениях в пространстве относительно поля напряжений в массиве пород и преобладающих структурных неоднородностях.

Проведение выработок с физической точки зрения можно представить как образование полости в массиве горных пород, обладающем определёнными свойствами и начальным (или естественным) полем напряжений. При этом вокруг выработки - полости формируется новое поле напряжений и смещений, являющееся результатом выемки породы при проведении горных работ.

В настоящее время основные закономерности формирования указанных полей напряжений достаточно детально изучены, разработаны экспериментальные и теоретические методы определения их параметров при условиях, отвечающим различным случаям горнотехнических ситуаций. При этом в большинстве случаев решения получены в предположении идеально упругого деформирования массива пород. Подобная постановка в малой степени отвечает реальным условиям деформирования массивов, но обладает огромным преимуществом, поскольку результаты определения напряжений являются максимально возможными.

Проследим основные закономерности изменения естественных полей напряжений при проведении горных выработок на простейших примерах.

В частности, простейшей формой сечения горных выработок является круговая. На практике её редко применяют для горизонтальных выработок, но для вертикальных стволов она широко распространена. В этом случае напряжения могут быть выражены весьма простыми формулами:

при равнокомпонентном поле естественных напряжений (s₁^¥ = s₃^¥)

a²

s_r = s₁^¥ (1 - -----);

r²

(3.1)

a²

s_q = s₁^¥ (1 + -----);

r²

при неравнокомпонентном поле естественных напряжений (s₁^¥¹ s₃^¥)

a²s₃^¥ + s₁^¥s₃^¥ + s₁^¥ a²

s_r = (1 - ----) [----------- + --------------- (1 - 3-----) cos 2q ];

r² 22 r²

s₃^¥ + s₁^¥ a² s₃^¥ - s₁^¥ a⁴

s_q = -----------(1 + ----) - ----------- (1 + 3-----) cos 2q ;(3.2)

2r²2r⁴

s₃^¥ - s₁^¥ a² a⁴

t_r_q = - -----------(1 + 2---- - 3------) sin 2q ;

2r²r⁴

где s₃^¥иs₁^¥ — компоненты тензора напряжений в нетронутом массиве горных пород; а — радиус сечения выработки; r, q— текущие полярные координаты.

Как следует из уравнений (3.1) и (3.2), напряжения в любой точке массива пород вокруг кругового сечения определяются соотношением напряжений в нетронутом массиве и координатами данной точки.

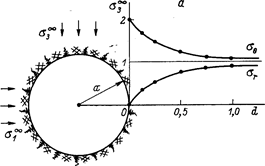
Причем в случае равномерного поля естественных напряжений (например, для вертикальных стволов при действии в массиве только гравитационных сил) коэффициент концентрации тангенциальных напряжений, т.е. коэффициент, показывающий во сколько раз напряжение в данной точке превышает соответствующее напряжение в нетронутом массиве (К = s_i / s^¥), в любой точке контура равен максимально К = 2 и все напряжения являются сжимающими (рис. 3.1).

Рис. 3.1. Распределение напряжений вокруг выработки кругового поперечного сечения при равнокомпонентном напряжённом состоянии нетронутого массива (s₃^¥ = s₁^¥).

При неравномерном поле напряжений (s₃^¥ ¹ s₁^¥) на части контура выработки со стороны действия большего из напряжений появляется область растягивающих напряжений, которая тем обширнее, чем больше разница между s₃^¥иs₁^¥. Сжимающие же напряжения в противоположность этому имеют большие значения со стороны действия меньших нагрузок.

Рассмотрим несколько частных случаев.

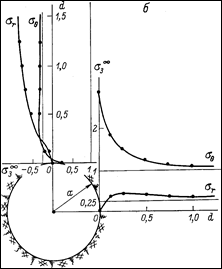
1. Естественное поле в массиве пород - гравитационное, соответствует гипотезе академика АН СССР А.Н. Динника, т.е. s₁^¥/s₃^¥ = n/(1-n). При n =0.2 горизонтальное напряжение s₁^¥ =0.25s₃^¥. Выработка горизонтальная (рис. 3.2).

Рис. 3.2. Распределение напряжений в кровле и стенках горизонтальной выработки кругового поперечного сечения при соотношениях компонент тензора напряжений в нетронутом массиве по А.Н. Диннику (при v = 0,2; s₁^¥ = 0.25 s₃^¥)

В этом случае максимальный коэффициент концентрации напряжений К наблюдается в боках выработки и составляет 2,75. В кровле образуется небольшая зона растяжений.

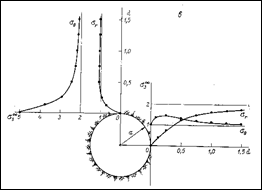
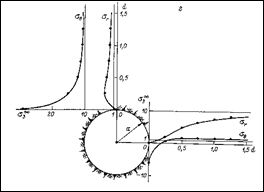
2. Естественное поле в массиве пород - гравитационно-тектоническое, т.е. горизонтальное напряжение s₁^¥ =2s₃^¥ (рис. 3.3а) и s₁^¥ =10s₃^¥(рис. 3.3б).

При этом максимальная концентрация напряжений наблюдается в кровле горизонтальной выработки, коэффициенты концентрации составляют соответственно 5 и 29.

Рис. 3.3. Распределение напряжений в кровле и стенках горизонтальной выработки кругового поперечного сечения при действии тектонических сил.

а - при s₁^¥ = 2 s₃^¥;б - при s₁^¥ = 10 s₃^¥).

Во всех рассмотренных случаях речь идет о коэффициенте концентрации тангенциальных напряжений, поскольку радиальные напряжения на контуре всегда равны нулю, если со стороны контура выработки массив не испытывает противодавления (например, реакции жесткой крепи).

Интересно проследить, как изменяется размер L области влияния выработок, т. е. другими словами, на каких расстояниях от контура выработки напряжения практически не отличаются от соответствующих компонент поля напряжений нетронутого массива.

Вычисления по формулам (3.2) показывают, что для условий равнокомпонентного (гидростатического) напряженного состояния нетронутого массива уже на расстоянии, немногим более трёх радиусов выработки [L = 1.65d (где d = 2a)], значения и тангенциальных и радиальных составляющих отличаются от соответствующих компонент напряжений в нетронутом массиве не более, чем на 5%.

Для других условий нагружения наблюдаются существенные различия в скорости затухания компонент напряжений s_q и s_r по мере удаления от контура выработки. При этом, как правило, быстрее затухают те компоненты, которые имеют большие коэффициенты концентраций на контуре.

Так, при s₁^¥=0.25s₃^¥наиболее быстро затухает тангенциальное напряжение s_q в стенке выработки, уже на расстоянии L = 1.35d от контура оно отличается на 5% от значения такового в нетронутом массиве. Остальные компоненты (в том числе и в кровле) затухают медленнее, и указанный уровень достигают лишь на расстоянии L = 2.75d.

При s₁^¥=2s₃^¥и s₁^¥=10s₃^¥тоже быстрее затухают s_q в кровле, исходя из этого, радиальная протяженность области влияния выработки составляет соответственно L = 1.5d. и L = 1.25d. Медленнее затухают радиальные составляющие напряжений. В частности, в стенке значение s_r в первом случаеотличается на 5% от уровня соответствующей компоненты нетронутого массива на расстоянии L = 2.5d от контура. Особенно медленно уменьшаются радиальные составляющие в кровле во втором случае (L = 7d).

Таким образом, размеры зоны влияния выработок существенно зависят от степени равномерности начального поля напряжений и минимально, при наиболее благоприятном случае, для круговой формы сечения составляют около полутора диаметров.

Представляет практический интерес характер распределения напряжений в массиве в сторону забоя выработки. В данном случае напряженное состояние массива уже нельзя отождествлять с распределением напряжений в плоскости продольного сечения выработки и необходимо рассматривать пространственную задачу. Результаты исследований свидетельствуют, что в самом простом случае, если конфигурацию забоя представить приближённо полусферой, а начальное поле напряжений в массиве является равнокомпонентным (гидростатическим) s₁^¥ = s₂^¥ = s₃^¥, компоненты напряжений определяются формулами в сферической системе координат (q; r; j)

s_q = s_j = s₁^¥[1 + a³ / 2 r³](3.3)

s_r = s₁^¥[1 - a³ / r³].

В этом случае (рис. 3.4) размеры зоны влияния и значения коэффициентов концентрации существенно меньше, чем для плоской постановки. В частности, уже на расстоянии L=0,8 d от контура выработки компоненты напряжении весьма мало отличаются от таковых в нетронутом массиве, а коэффициент концентрации тангенциальных напряжений на контуре К = 1,5.

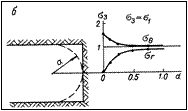
Рис. 3.4. Распределение напряжений вокруг забоя выработки кругового поперечного сечения.

Чтобы проследить, как изменяются напряжения в массиве пород в зависимости от формы сечений выработок, рассмотрим случаи, когда выработки имеют эллиптические, прямоугольные и сводчатые поперечные сечения.

В практике горного дела эллиптическую форму поперечного сечения иногда применяют для вертикальных стволов.

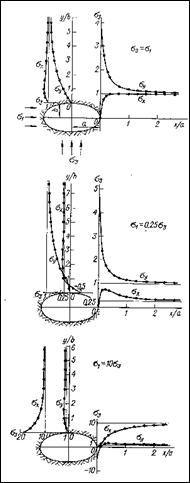
На рис. 3.5 представлены графики напряжений вокруг эллиптического отверстия с отношением осей а/б = 2, при тех же соотношениях компонент начального напряженного состояния, как и для круговой формы сечения выработок.

Из сопоставления графиков на рис. 3.2; 3.3; и 3.5 следует, что в целом характер распределения напряжений вокруг эллиптического отверстия подобен таковому при круговом сечении. Однако коэффициенты концентрации тангенциальных напряжений s_q отличаются от соответствующих им коэффициентов при круговой форме.

По сравнению с круговой формой сечения выработок эллиптическое сечение характеризуется несколько большими скоростями затухания напряжений по мере удаления в сторону массива, т. е. меньшей областью влияния. В частности, для наиболее благоприятных случаев, размеры области влияния эллиптического сечения составляют около 1.2 большого диаметра (разница между напряжениями на границе области влияния и в нетронутом массиве не превышает 5%).

Рис. 3.5. Распределение напряжений в стенках выработки эллиптического поперечного сечения с соотношением осей а/б=2 при различных компонентах тензора напряжений в нетронутом массиве.

На напряжения вокруг выработки эллиптического сечения влияют соотношение полуосей сечения и (что особенно важно) ориентировка осей сечения в поле напряжений s₁^¥ и s₃^¥нетронутого массива.

Фактически, это один из элементов управления состоянием приконтурного массива вокруг выработок в случае их эллиптического сечения:

Максимальная устойчивость выработки достигается при соблюдении равенства а/б = s₃^¥/ s₁^¥ и при расположении большей оси сечения по линии действия наибольшего из напряжении в нетронутом массиве.

Это необходимо иметь в виду при проектировании горных выработок, выборе их оптимальных направлений и ориентации поперечного сечения.

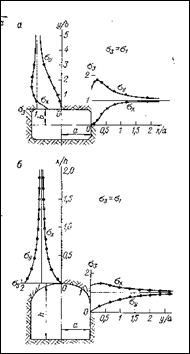
Отмеченные закономерности можно проследить и при рассмотрении графиков напряжений вокруг сечений выработок прямоугольной и сводчатой формы (рис. 3.6). Однако в этих случаях напряжения уже не могут быть представлены в виде элементарных уравнений, и их вычисляют с помощью более сложных математических методов.

Рис. 3.6. Распределение напряжений в стенках выработки прямоугольной (а) и сводчатой (б) форм поперечного сечения.

Если в качестве модели массива применяется анизотропная упругая модель, в частности, модель трансверсально-изотропного тела, то характер распределения напряжений вокруг выработок изменяется.

В настоящее время разработана теория упругости анизотропной среды, позволяющая вычислять напряжения вокруг отверстий различной конфигурации, однако лишь отдельные решения доведены непосредственно до числа. При этом имеющиеся данные об анизотропии упругих свойств пород свидетельствуют о незначительных отличиях значений напряжений вокруг выработок в анизотропных массивах от изотропного случая.

Теоретические работы о распределении напряжений в физически нелинейных упругих средах показывают, что при этом коэффициенты концентрации напряжений вокруг отверстий различной формы, в отличие от случая линейного деформирования, существенно зависят от упругих характеристик среды и значений внешних нагрузок.

Физическая нелинейность среды приводит к более равномерному распределению напряжений возле отверстий вследствие понижения коэффициента концентрации напряжений в наиболее нагруженных точках сечения. К выравниванию поля напряжений вокруг выработок приводит, в частности, и пластическое деформирование пород. Если породы проявляют пластические свойства, непосредственно вокруг контура выработки формируется область пластических деформаций.

Таким образом, упругие решения можно рассматривать как верхний предел возможных напряжений в реальных массивах горных пород, обеспечивающий некоторый запас в инженерных расчётах. Величина этого запаса тем большая, чем больше реальные свойства массива отличаются от свойств идеально упругой среды.

На современных горных предприятиях лишь сравнительно небольшая часть выработок — одиночные, которые не испытывают влияния соседних выработок. Это обычно капитальные выработки — вскрывающие (стволы, штольни) и подходные (квершлаги, уклоны и др.) и в меньшей степени подготовительные. Большую же часть выработок проводят на небольших расстояниях друг от друга, определяемых параметрами применяемой системы разработки. В результате взаимного влияния напряженное состояние пород вокруг таких выработок существенно изменяется.

Теоретическое определение напряжений вокруг системы сближенных выработок является более сложной задачей, чем для одиночной выработки, но и в этом случае могут быть применены методы теории упругости, разработаны также и приближенные методы решения подобных задач.

Результаты теоретического изучения, а также практический опыт проведения и эксплуатации горных выработок позволяют заключить, что напряжения вокруг взаимовлияющих выработок зависят от их размеров, конфигурации, размеров целиков между ними, пространственного расположения по отношению друг к другу, от числа сближенных выработок, а также от параметров начального поля напряжений в нетронутом массиве.

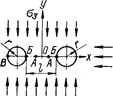
Прежде всего, рассмотрим достаточно простой случай, когда на близком расстоянии друг от друга в массиве пройдены две одинаковые параллельные выработки с поперечными сечениями круговой формы (рис. 3.7, 3.8).

Очевидно, что взаимное влияние выработок теоретически начнет сказываться, когда расстояния между их контурами будет меньше трех диаметров.

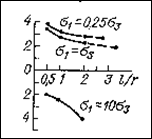
Рис. 3.7. Тангенциальные напряжения s_q (в долях s₃) в стенках (точка Б) сближенных выработок на одном горизонте в зависимости от ширины целика между ними при различном напряженном состоянии нетронутого массива.

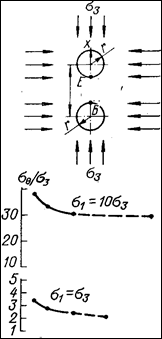
Рис. 3.8. Тангенциальные напряжения s_q (в долях s₃) в кровле и почве (точка Б) сближенных выработок на разных горизонтах в зависимости от расстояния между их центрами при различном напряженном состоянии нетронутого массива.

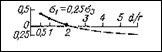
Из рис. 3.7 и 3.8 видно, что при сближенных выработках тангенциальные напряжения s_q на их контуре могут увеличиваться в 2 раза и более, при этом напряжение s_q в точке Брастет особенно быстро, когда ширина целика становится меньше радиуса выработок. Исключение представляет случай, когда действуют высокие горизонтальные напряжения тектонического происхождения. Тогда напряжения в целике и на контуре выработок уменьшаются или даже могут измениться по знаку.

Существенную роль играет ориентация максимального главного сжимающего напряжения нетронутого массива по отношению к системе выработок. Если оно действует вдоль линии центров сечений выработок, то при сближении выработок концентрация напряжений в целике убывает (при s₁ = 10s₃ на рис. 3.7). Если же оно направлено перпендикулярно к линии центров, то концентрация напряжений в целике возрастает (при s₁ = 0.25s₃ на рис. 3.7 и s₁ = 10s₃ на рис. 3.8).

Отсюда ещё один элемент управления состоянием массива:

В массивах с негидростатическим распределением напряжений или при ярко выраженной анизотропии упругих свойств пород парные сближенные выработки целесообразно располагать таким образом, чтобы линия их центров совпадала с направлением наибольшего главного напряжения или с направлением в массиве, по которому модуль упругости имеет максимальное значение (например, для слоистого массива - перпендикулярно к слоистости).

При увеличении числа сближенных выработок отмеченные закономерности сохраняются, изменяются лишь фактические значения действующих напряжений. В частности, в наиболее неблагоприятном случае при условиях, приближающихся к одноосному сжатию поперек линии центров системы из достаточно большого числа выработок, напряжение s_q на контуре каждой из них может достигать пятикратного значения по отношению к одиночной выработке (при ширине целика l=0,2r).

Особое значение для практики имеет случай, когда поперечные сечения взаимовлияющих выработок существенно различны.

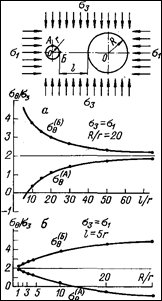
Поскольку область влияния одиночной выработки прямо пропорциональна радиусу сечения выработки, очевидно, что наиболее ощутимо влияние сближенных выработок скажется на распределении напряжений вокруг выработки меньшего сечения. На рис. 3.9 приведены зависимости напряжения s_q на контуре выработки меньшего сечения в точках А и Б от размера целика между сближенными выработками при фиксированном отношении радиусов их сечений (R/r = 20), а также от отношения радиусов R/r при постоянной ширине целика (l=5 r) в условиях гидростатического напряженного состояния нетронутого массива.

Из рис. 3.9 следует, что в точках контура малой выработки, располагающихся вблизи линии, соединяющей центры обеих выработок, тангенциальные напряжения s_q могут увеличиваться в 2 — 2,5 раза; при этом наиболее интенсивно они растут в диапазоне отношения радиусов выработок до 20. В то же время в точках контура,

Рис. 3.9. Тангенциальные напряжения s_q (в долях s₃) на контуре выработки (точки A и Б) в зависимости от ширины целика (а) и при различных соотношениях радиусов сближенных выработок (б).

расположенных под прямым углом к линии центров, напряжения s_q уменьшаются, вплоть до смены их знака.

Влияние выработки большего сечения начинает существенно сказываться при ширине целика между выработками l³1 - l,5D (где D=2R). Выработка меньшего сечения на напряжения вокруг выработки большего сечения практически не влияет.

В тех случаях, когда подготовительная выработка попадает в область влияния очистной выработки камерного типа, расстояние, на котором начнет сказываться влияние последней, будет меньшим, чем соответствующие расстояния в рассмотренном примере. Это объясняется существенно меньшими (почти в 2 раза) размерами области влияния изометрической выработки по сравнению с цилиндрической.

Рассмотренные закономерности распределения напряжений вокруг сближенных выработок позволяют заключить, что в большинстве случаев взаимное влияние выработок проявляется в увеличении тангенциальных напряжений s_q.

Отсюда элементы управления состоянием массива:

<123 4 5 6 7 >

Дата добавления: 2015-12-26; просмотров: 1835;