Вычисление линейных невязок по осям координат
Находят суммы вычисленных приращений
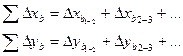
И теоретические суммы приращений
ΣΔхт=хкон–хнач
ΣΔут=укон–унач
Линейные невязки по осям координат
fx= Σ∆хф– Σ∆хт
fу= Σ∆уф–Σ∆ут
Вычисление абсолютной и относительной невязок теодолитного хода
fабс = 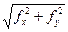
Определяют относительную линейную невязку fотн теодолитного хода: fотн= 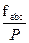
где Р – периметр хода.
Допустимое значение относительной невязки не должно превышать погрешности линейных измерений 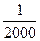 . Если это условие нарушено, то длины линий перемеряют, а если выполняется, то вычисляют поправки в вычисления координат:
. Если это условие нарушено, то длины линий перемеряют, а если выполняется, то вычисляют поправки в вычисления координат:
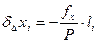
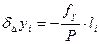
Поправки округляют до 0.01 мм и выписывают их со своими знаками над соответствующими приращениям ∆х и ∆у.
Сумма поправок должна равняться невязке с обратным знаком:
ΣδΔx=–fx
ΣδΔy=–fy
Вычисляют исправленные приращения координат и записывают результаты в ведомость:
∆хиспр= ∆хвыч + δΔх
∆уиспр= ∆увыч + δΔу
Для контроля определяют суммы исправленных приращений координат, которые должны быть равны теоретическим суммам приращений:
∆хиспр= Σхт
∆уиспр= Σут
Дата добавления: 2015-12-22; просмотров: 1254;
