Камеральная обработка результатов измерения теодолитного хода
Вычисление координат точек теодолитного хода.
Перед началом вычисления проверяют все журналы (значения вычисленных горизонтальных и вертикальных углов, горизонтальных проложений). Уравнивают горизонтальные углы, для этого вычисляют сумму измеренных горизонтальных углов:
Σβф=β1+β2+…+βn
Вычисляют теоретическую сумму углов
Σβт=180º(n–2) – для замкнутого хода
Σβт=αнач– αкон±180º∙n – для разомкнутого хода
n – число измеренных углов
Вычисляют угловую невязку: fβ= Σβф– Σβт сравнивая ее с допустимой: fβ доп =1.5t 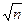
где t–точность отсчетного приспособления теодолита.
Невязка fβ по абсолютной величине не должна превышать допустимого значения fβ доп, в противном случае углы измеряют заново. Если условие вычисляют поправку в каждый угол и записывают в ведомость над значениями измеренных углов: δβ=– fβ/n.
Контролем правильности распределения невязки служит равенство: Σδβ=– fβ
Исправленные углы вычисляют по формуле: βi испр= βi изм + δβ i
Для контроля подсчитывают сумму исправленных углов, которая должна быть равна теоретической сумме углов: Σβиспр= Σβт
Примычный угол βприм не исправляют.
Вычисление дирекционных углов и румбов.
По исходному дирекционному углу αпт–I и исправленным значениям углов определяют дирекционные углы сторон теодолитного хода:
αn=αn–1±180º–βn – для правых углов
αn=αn–1±180º+βn – для левых углов
Контролем правильности вычислений дирекционных углов является совпадение значения дирекционного угла начальной стороны αI–II:
αI–II= αпт–1±180º–βпр=αV–I±180º–β1
Вычисляют румбы
| № четв. | Дирекционный угол | Назв. румба | Формулы | Знаки приращения | |
| ∆x | ∆y | ||||
| I | 0º–90º | СВ | r=α | + | + |
| II | 90º–180º | ЮВ | r=180º–α | – | + |
| III | 180º–270º | ЮЗ | r=α–180º | – | – |
| IV | 270º–360º | СЗ | r=360º–α | + | – |
Вычисление приращений координат
По значениям дирекционных углов и горизонтальными проложениям сторон теодолитного хода вычисляют приращения координат с точностью до 0.01м:
∆х=d·cos r
∆у=d·sin r
Знаки приращения координат определяют в зависимости от названия румба.
Дата добавления: 2015-12-22; просмотров: 1165;
