Перенос теплоты теплопроводностью при стационарном режиме

Однородная плоская стенка. Простейшей и очень распространенной задачей, решаемой теорией теплообмена, является определение плотности теплового потока, передаваемого через плоскую стенку толщиной δ , на поверхностях которой поддерживаются температуры t_c1 и t_c2 (рис. 8.2). Температура изменяется только по толщине пластины — по одной координате х. Такие задачи называются одномерными, решения их наиболее просты, Учитывая, что для одномерного случая

,

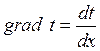и используя основной закон теплопроводности , получаем дифференциальное уравнение стационарной теплопроводности для плоской стенки: 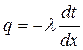. В стационарных условиях, когда энергия не расходуется на нагрев, плотность теплового потока q неизменна по толщине стенки.

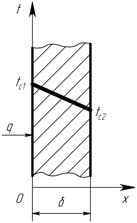
Рис. 9.1 Стационарное распределение температуры по толщине плоской стенки

В большинстве практических задач приближенно предполагается, что коэффициент теплопроводности l к не зависит от температуры и одинаков по всей толщине стенки. Значение l находят в справочниках при температуре 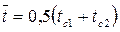, средней между температурами поверхностей стенки При 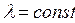, , 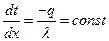т. е. зависимость температуры t от координаты x линейна (рис. 9.1).

Разделив переменные в последнем уравнении и проинтегрировав по t от t_c1 до t_c2 и по х от 0 до δ:

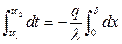
получим зависимость для расчета плотности теплового потока 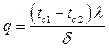или .

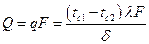Полученная простейшая формула имеет очень широкое распространение в тепловых расчетах. По этой формуле не только рассчитывают плотности теплового потока через плоские стенки, но и делают оценки для случаев более сложных, упрощенно заменяя в расчетах стенки сложной конфигурации на плоскую. Иногда уже на основании оценки тот или иной вариант отвергается без дальнейших затрат времени на его детальную проработку.

С помощью этой формул можно рассчитать коэффициент теплопроводности материала, если экспериментально замерить тепловой поток и разность температур на поверхностях пластины (стенки) известных размеров.

Отношение 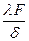называется тепловой проводимостью стенки, а обратная величина 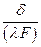тепловым или термическим сопротивлением стенки и обозначается 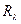. Пользуясь понятием термического сопротивления, формулу для расчета теплового потока можно представить в виде

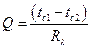аналогичном закону Ома в электротехнике (сила электрического тока равна разности потенциалов, деленной на электрическое сопротивление проводника, по которому течет ток). Очень часто термическим сопротивлением называют величину 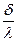, которая равна термическому сопротивлению плоской стенки площадью 1 м².

Многослойная стенка. Формулой для определения теплового потока можно воспользоваться для расчета через стенку, состоящую из нескольких плотно прилегающих друг к другу слоев разнородных материалов (рис. 9.2). Например, кирпичную стенку здания, покрытую слоем штукатурки, краски и т. д. Термическое сопротивление такой стенки равно сумме термических сопротивлений отдельных слоев: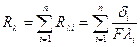

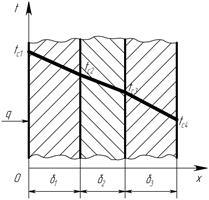
Рис. 9.2 Распределение температуры по толщине многослойной плоской стенки.

В формулу теплового потока нужно подставить разность температур в тех точках (поверхностях), между которыми «включены» все суммируемые термические сопротивления, т. е. в данном случае 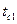и :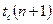

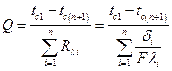
Последнее выражение легко получить, записав разность температур по формуле 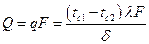для каждого из п слоев многослойной стенки и сложив все п выражений с учетом того, что во всех слоях Q имеет одно и то же значение. При сложении все промежуточные температуры сократятся.

Распределение температур в пределах каждого слоя—линейное, однако в различных слоях крутизна температурной зависимости различна, поскольку согласно формуле 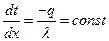. Плотность теплового потока, проходящего через все слои, в стационарном режиме одинакова, а коэффициент теплопроводности слоев различен, следовательно, более резко температура меняется в слоях с меньшей теплопроводностью. Так, в примере на рис. 9.2 наименьшей теплопроводностью обладает материал второго слоя, а наибольшей — третьего.

Рассчитав тепловой поток через многослойную стенку, можно определить падение температуры в каждом слое по соотношению 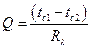и найти температуры на границах всех слоев. Это очень важно при использовании в качестве теплоизоляторов материалов с ограниченной допустимой температурой. Обобщенную формулу для расчета температуры 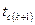за любым слоем 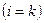можно получить из выражения

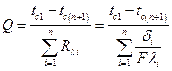, подставив в него n = k: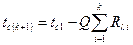

Контактное термическое сопротивление. Идеально плотный контакт между отдельными слоями многослойной стенки получается, если один из слоев наносят на другой в жидком состоянии или в виде текучего раствора (цементного, гипсового и др.). Твердые тела касаются друг друга только вершинами профилей шероховатостей. Площадь контакта вершин пренебрежимо мала, и весь тепловой поток идет через воздушный зазор. Это создает дополнительное (контактное) термическое сопротивление R_k. Его можно приближенно оценить, если принять, что толщина зазора между соприкасающимися телами δ в среднем вдвое меньше максимального расстояния 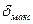между впадинами шероховатостей. Так, при контакте двух пластин с шероховатостью поверхности 5 класса (после чистовой обточки, строгания, фрезерования) 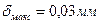и в воздухе комнатной температуры 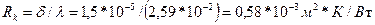. Это эквивалентно термическому сопротивлению слоя стали толщиной около 30 мм.

Для уменьшения контактного сопротивления необходимо заполнять зазоры каким-либо материалом с более высокой, чем у воздуха, теплопроводностью, например спаять или хотя бы склеить поверхности.

Цилиндрическая стенка. Очень часто теплоносители движутся по трубам и требуется рассчитать тепловой поток, передаваемый через цилиндрическую стенку трубы. Задача о распространении теплоты в цилиндрической стенке при известных и постоянных температурах на внутренней и наружной поверхностях, также одномерная, если ее рассматривать в цилиндрических координатах. Температура изменяется только вдоль радиуса (по координате r), а по длине трубы и по ее периметру остается неизменной. В этом случае 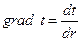и закон Фурье будет иметь вид

,

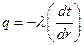или для трубы длиной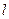

.

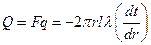Интегрировать удобно уравнение (8.15), так как тепловой поток не меняется по толщине стенки, a 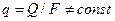, поскольку площадь 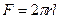, через которую проходит тепловой поток, зависит от радиуса.

Разделим переменные:

Интеграл последнего уравнения

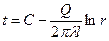
показывает, что распределение температуры по радиусу стенки подчиняется логарифмическому распределение температуры по радиусу стенки подчиняется логарифмическому закону (рис.9.3).

Рис. 9.3 Изменение температуры по толщине однослойной цилиндрической стенки

У внутренней поверхности, где кривизна стенки больше, температура меняется резче, чем у наружной.

Интегрирование в определенных пределах (по t от t_c1 до t_c2 и по r от r₁ до r₂) дает зависимость для расчета теплового потока через цилиндрическую стенку:

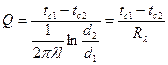
Для труб обычно измеряется и приводится в условиях задач диаметр, а не радиус, поэтому отношение радиусов 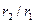заменено отношением диаметров .

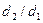Термическое сопротивление для цилиндрической стенки имеет вид

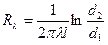
причем при 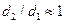расчет должен проводиться с высокой точностью, поскольку небольшая погрешность, допущенная при определении отношения 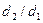, в этом случае дает значительную ошибку при вычислении логарифма. Например, если значение 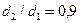округлить до 1,1 (погрешность округления меньше 1 %), погрешность вычисления логарифма, а следовательно, и теплового потока будет больше 10%. С другой стороны, оказывается, что при отношении 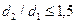погрешность определения термического сопротивления цилиндрической стенки по формуле 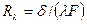справедливой для плоской стенки [поверхность трубы считается по среднеарифметическому диаметру 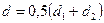, дает ошибку меньше 1,5 %. Более высокая точность в практических расчетах требуется редко.

Для определения теплового потока через многослойную цилиндрическую стенку следует, как и для многослойной плоской стенки, просуммировать термические сопротивления отдельных слоев:

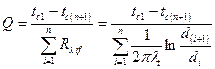
отличие предыдущей формулы от

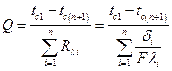
заключается только в способе расчета термических сопротивлений отдельных слоев для плоской и цилиндрической стенок. Но и это различие существенно только при больших отношениях наружного и внутреннего диаметров каждого слоя .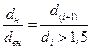

При меньших отношениях 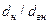термические сопротивления отдельных слоев, как уже было показано, целесообразнее считать по упрощенной формуле, справедливой для плоской стенки:

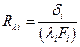
Расчет температур на границах слоев в данном случае осуществляется так же, как для многослойной плоской стенки:

.

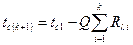Лекция № 10

Тема : «Конвективный теплообмен.»(2 часа)

1 ПЛАН

1. Основной закон конвективного теплообмена. Пограничный слой.

2.Основы теории подобия и моделирования.

3. Теплоотдача при вынужденном движении теплоносителя.

4. Теплоотдача при свободной конвекции.

5. Теплоотдача при изменении агрегатного состояния.

2. ЛИТЕРАТУРА

Основная литература

1. Амерханов Р.А., Драганов Б.Х. Теплотехника. - М.: Энергоатомиздат, 2006. – 432 с.

2. Круглов Г.А., Булгакова Р.И., Круглова Е.С. Теплотехника. – СПб.: Издательство «Лань», 2010. – 208 с.

Дополнительная литература

1. Теплотехника. /А.П. Баскаков, Б.В. Берг и др. – М.: Энергатомиздат, 1991. – 224 с.

2. Техническая термодинамика. / Кириллин В.А., Сычев В.В., Шейндлин А.Е. – М.: Издательский дом МЭИ, 2008. – 496 с.