Основной закон теплопроводности
В основной закон теплопроводности входит ряд математических понятий, определения которых целесообразно напомнить и пояснить.
Температурное поле — это совокупность значений температуры во всех точках изучаемого пространства в данный момент времени. Математически оно описывается в виде 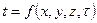 . Различают стационарное температурное поле, когда температура во всех точках тела не зависит от времени, и нестационарное. Кроме того, если температура изменяется только по одной или двум пространственным координатам, то температурное поле называют соответственно одно- или двухмерным.
. Различают стационарное температурное поле, когда температура во всех точках тела не зависит от времени, и нестационарное. Кроме того, если температура изменяется только по одной или двум пространственным координатам, то температурное поле называют соответственно одно- или двухмерным.
Изотермическая поверхность - это геометрическое место точек, температура в которых одинакова.
Градиент температуры — grad t есть вектор, направленный по нормали к изотермической поверхности и численно равный производной от температуры по этому направлению.
Фурье установил, что количество теплоты dQt, проходящее через элемент поверхности dF за промежуток времени dt, пропорционально температурному градиенту 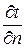 :
:
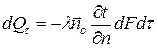 .
.
Так как 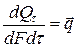 (плотность теплового потока), то
(плотность теплового потока), то
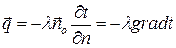 Þ
Þ 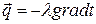 .
.
Полученное уравнение является математической записью основного закона теплопроводности, который формулируется следующим образом: плотность теплового потока прямо пропорциональна градиенту температуры.
Опытным путем установлено, что коэффициент пропорциональности в уравнении Фурье есть физический параметр вещества. Он характеризует способность вещества проводить теплоту и называется коэффициентом теплопроводности, Вт/(м×К).
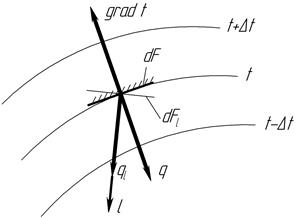
Вектор плотности теплового потока 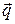 направлен по нормали к изотермической поверхности. Его положительное направление совпадает с направлением убывания температуры, так как теплота всегда передается от более горячих частей тела к холодным. Таким образом, векторы
направлен по нормали к изотермической поверхности. Его положительное направление совпадает с направлением убывания температуры, так как теплота всегда передается от более горячих частей тела к холодным. Таким образом, векторы 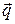 и
и 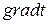 лежат на одной прямой, но направлены в противоположные стороны. Это и объясняет наличие знака «минус» в уравнении Фурье.
лежат на одной прямой, но направлены в противоположные стороны. Это и объясняет наличие знака «минус» в уравнении Фурье.
| Скалярная величина вектора плотности теплового потока будет равна:
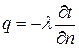 .
Плотность теплового потока ql в любом другом направлении l равна проекции вектора .
Плотность теплового потока ql в любом другом направлении l равна проекции вектора 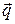 на это направление l: на это направление l:
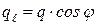 . .
|
Тепловой поток Q в единицу времени через элементарную площадку dF будет равен:
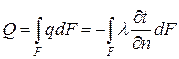 .
.
Полный тепловой поток Qt за время t через элементарную площадку dF равен, Дж:
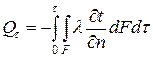 .
.
Количество теплоты, проходящее через элементарную площадку dFl за время dt, будет равно:
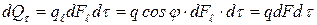 ,
,
так как 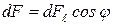 .
.
Таким образом, для определения количества теплоты, проходящего через какую-либо поверхность твердого тела, необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и является главной задачей аналитической теории теплопроводности.
Дата добавления: 2015-11-26; просмотров: 818;
