Графические редакторы. Понятие о векторной и растровой графике.

Компьютерные программы для работы с изображениями могут быть основаны на создании либо векторной графики, либо растровых изображений.

Векторные изображения, также называемые объектно-ориентированными или иллюстрациями, определяются математически как наборы точек, соединенных линиями. Графические элементы векторного файла называются объектами. Каждый объект представляет из себя самостоятельную систему и обладает такими свойствами, как цвет, форма, контур, размер и положение на экране, включенными в его описание.

Поскольку каждый объект является самостоятельной системой, можно перемещать его и изменять его свойства, сохраняя при этом первоначальное качество и четкость изображения, и не влияя на другие объекты иллюстрации. Эти свойства делают векторные программы идеальными для иллюстративного и трехмерного моделирования, где в процессе работы часто требуется создавать отдельные объекты и манипулировать ими.

Векторные иллюстрации не зависят от разрешения. Это означает, что они всегда отображаются с максимальным разрешением, которого позволяет достичь устройство вывода (например, принтер или монитор). В результате качество иллюстрации, напечатанной на принтере с разрешением 600 точек на дюйм, будет выше, чем на принтере с разрешением 300 точек на дюйм.

Растровые изображения, также называемые рисованными, состоят из отдельных точек (элементов изображения), называемых пикселями, которые создают узор за счет различного положения и окраски. При увеличении изображения можно увидеть составляющие его отдельные квадратики. Увеличение размера растрового изображения происходит за счет увеличения каждого элемента, что огрубляет все линии и формы.

Однако при большем удалении цвет и форма растрового изображения будут выглядеть сплошными. Поскольку каждый элемент изображения имеет собственный цвет, можно создавать фотографические эффекты, такие как затенение и усиление цвета, изменяя выбранную область по одному элементу.

Уменьшение размера растрового изображения также искажает начальный вид, поскольку для уменьшения общего размера изображения часть его элементов удаляется. Кроме того, поскольку растровое изображение создано из упорядоченно расставленных пикселей, нельзя манипулировать его отдельно взятыми частями (т.е. перемещать их).

При работе с несколькими приложениями пакета CorelDRAW 7 или при необходимости работать с ними попеременно, имеется Программа запуска приложений. Кнопка Программы запуска приложений находится в каждом из приложений и позволяет запускать другие программы, не отыскивая их в системе.

При работе с растровыми изображениями качество результата зависит от выбранных на начальной стадии процесса параметров разрешения. Разрешение – это общий термин, относящийся к количеству элементов и информации, содержащейся в файле изображения, а также к уровню детализации, который может обеспечить устройство ввода, вывода или отображения. При работе с растровыми изображениями разрешение влияет как на качество результата работы, так и на размер файла.

Работа с растровыми изображениями требует некоторого расчета, поскольку выбранное разрешение изображения обычно сохраняется вместе с файлом. Печатаете ли вы растровый файл на лазерном принтере с разрешением 300 точек на дюйм, или на фотонаборном автомате с разрешением 1270 точек на дюйм, он будет напечатан с тем разрешением, которое было установлено при создании изображения, если оно не выше разрешения принтера.

Для того, чтобы результирующее изображение выглядело так же, как оно выглядит на экране, следует перед началом работы настроить разрешение изображения в соответствии с разрешением различных устройств.

CorelDRAW является векторным графическим редактором, однако он позволяет включать растровые изображения в иллюстрации и экспортировать созданные растровые изображения.

23. Элементы поддержки принятия решений в EXCEL: подбор параметра.

Подбор параметра – это инструмент Excel, позволяющий целенаправленно перебрать множество значений одиночного параметра с одновременным контролем результирующего значения.

По сути, этот механизм "подгоняет" исходные данные под желаемый ответ. При этом очередное значение параметра подставляется в формулу, выполняется вычисление, и полученный результат сравнивается с искомым (целевым) значением. Если на очередном шаге вычислений разница между текущим результатом и целевым значением стала меньше заданной величины, т.е. достигнута заданная точность решения, то вычисления прекращаются, и текущее значение предлагается как итоговый результат подбора.

Для нахождения корня функции решают уравнение f(x) = 0.

Для решения уравнения с помощью средства Excel Подбор параметра сперва надо выполнить следующие преобразования: в левую часть уравнения перенести все неизвестные, в правой части можно оставить только константу или ноль.

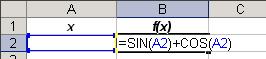
Например, уравнение x³+3x² = 8x+2 должно быть преобразовано к виду: x³+3x^{2 –} 8x = 2, а для нахождения корня функции f(x) = sinx+cosx следует решить уравнение sinx+cosx = 0.

Затем, в Excel одну ячейку отводят под искомое неизвестное значение x, а в другую заносят формулу для левой части уравнения, ссылаясь вместо x на отведенную ячейку.

Далее, чтобы найти заданное значение формулы, изменяя значение отдельной влияющей ячейки дают команду: пункт меню Сервис ® Подбор параметра.

На экране появляется диалоговое окно (рис. 18), где

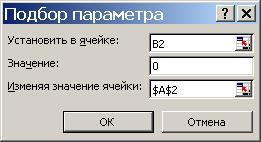
- в поле Установить в ячейке указывают адрес ячейки, которая содержит формулу;

- в поле Значение указывают число, которое надо получить по формуле;

- в поле Изменяя ячейку указывают адрес изменяемой ячейки (влияющей на формулу).

Для решения нажимают кнопку OK . Если процесс не сходится, то с помощью кнопок Пауза и Шаг можно регулировать подбор параметра.

Замечание. При подборе параметра практически всегда получаются приближенные значения результата с точностью, достаточной для типичных экономических задач. В то же время, если речь идет о высокоточных инженерных или научных вычислениях точность полученных результатов может быть недостаточна. А для уравнений, имеющих несколько решений, Подбор параметра находит только одно решение, ближайшее к первоначальному значению подбираемого параметра. Если надо найти корень функции на отрезке, в качестве начального значения параметра следует задавать левый конец отрезка.

24. Элементы поддержки принятия решений в EXCEL: поиск решения.

Поиск решения – представляет собой набор управляемых пользователем алгоритмов решения оптимизационных задач. При поиске решения целенаправленному изменению подвергаются несколько параметров (ячеек). Кроме того, на диапазоны изменения параметров могут быть наложены ряды ограничений, которые выражаются в виде формул, описывающих отношения (системы уравнений) между значениями параметров и некоторыми величинами. Значения целевой функции получаются в результате вычисления формулы, расположенной в отдельной целевой ячейке, которая должна быть обязательно связана с изменяемыми параметрами.

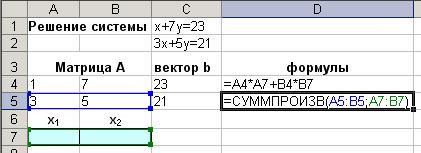
Для решения системы линейных алгебраических уравнений с помощью средства Excel Поиск решения надо занести в отдельные ячейки Excel матрицу коэффициентов при неизвестных и вектор свободных членов. Затем для искомых неизвестных значений x_i отводят i ячеек. Далее в отдельный столбец заносят формулы для левой части уравнений системы, ссылаясь вместо x_i на отведенные ячейки. При этом может быть использована встроенная функция СУММПРОИЗВ(массив1; массив2), где массив1 – строка матрицы коэффициентов А, массив2 – диапазон ячеек, отведенных для x_i.

Чтобы решить систему дают команду: пункт меню Сервис ® Поиск решения.

На экране появится диалоговое окно, в котором следует задать параметры.

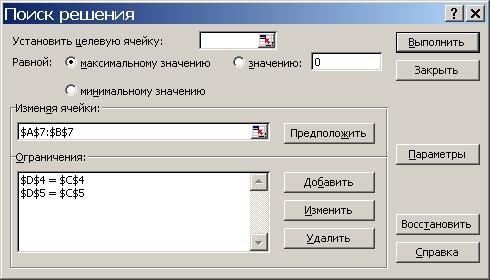
По окончании нажимают экранную кнопку Выполнить . В результате появится окно, в котором сохраняют найденное решение нажатием кнопки OK .

Замечание 1. При решении системы уравнений целевая ячейка не задается. Ввод ограничений осуществляется экранной кнопкой Добавить .

Замечание 2. Поиск решения может быть применен и для решения нелинейный систем уравнений. В этом случае экранной кнопкой Параметры (рис. 20) вызывается диалоговое окно «Параметры поиска решения», в котором отключают флажок Линейная и устанавливают вид оценки – Квадратичная, которая служит для использования квадратичной экстраполяции, дающей лучшие результаты при решении нелинейных задач.

25. EXCEL: простейшие операции, выполняемые в VBA, вставка модулей и процедур. Создание пользовательских функций.

1. Запустить VBAможно:

ü или через Alt+F11; это же сочетание клавиш переводит нас из VBAна рабочий лист

ü или пункт меню Сервис, Макрос, Редактор Visual Basic