Электромагнитные волны
Электромагнитные волны в двухпроводной линии
Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений. Эта теория объяснила все известные в то время экспериментальные факты и предсказала ряд новых явлений, существование которых подтвердилось впоследствии. Основным следствием теории Максвелла был вывод о существовании электромагнитных волн, распространяющихся со скоростью света. Теоретическое исследование свойств этих волн привело Максвелла к созданию электромагнитной теории света.
Основу теории образуют уравнения Максвелла. В учении об электромагнетизме эти уравнения играют такую же роль, как законы Ньютона в механике или основные законы (начала) в термодинамике.
Первую пару уравнений Максвелла образуют уравнения:
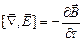 , (1)
, (1)
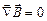 . (2)
. (2)
Первое из этих уравнений связывает значение  с изменениями вектора
с изменениями вектора  во времени и является по существу выражением закона электромагнитной индукции. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов.
во времени и является по существу выражением закона электромагнитной индукции. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов.
Вторую пару уравнений Максвелла образуют уравнения:
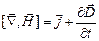 , (3)
, (3)
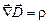 . (4)
. (4)
Первое уравнение устанавливает связь между токами проводимости и порождаемым ими магнитным полем. Второе показывает, что источниками вектора 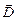 служат сторонние заряды.
служат сторонние заряды.
Уравнения (1) – (4) представляют собой уравнения Максвелла в дифференциальной форме. В первую пару уравнений входят только основные характеристики поля: 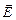 и
и 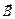 . Во второй же паре фигурируют только вспомогательные величины
. Во второй же паре фигурируют только вспомогательные величины 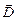 и
и 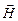 .
.
Каждое из векторных уравнений (1) и (3) эквивалентно трем скалярным уравнениям, связывающим компоненты векторов, стоящих в левой и правой частях равенств. Представим уравнения Максвелла в скалярной форме:
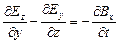 ,
, 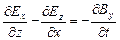 ,
, 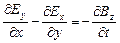 , (5)
, (5)
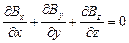 (6)
(6)
(первая пара уравнений),
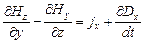 ,
, 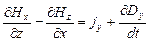 ,
, 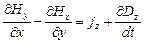 , (7)
, (7)
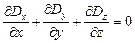 (8)
(8)
(вторая пара уравнений).
Всего получилось 8 уравнений, в которые входят 12 функций (по три компоненты векторов 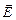 ,
, 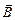 ,
, 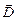 ,
, 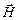 ) Поскольку число уравнений меньше числа неизвестных функций, уравнений (1) – (4) недостаточно для нахождения полей по заданным распределениям зарядов и токов. Чтобы осуществить расчет полей, нужно дополнить уравнения Максвелла уравнениями, связывающими
) Поскольку число уравнений меньше числа неизвестных функций, уравнений (1) – (4) недостаточно для нахождения полей по заданным распределениям зарядов и токов. Чтобы осуществить расчет полей, нужно дополнить уравнения Максвелла уравнениями, связывающими 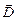 и
и 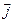 с
с 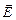 , а также
, а также 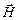 с
с 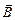 . Эти уравнения имеют вид:
. Эти уравнения имеют вид:
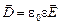 , (9)
, (9)
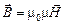 , (10)
, (10)
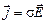 (11)
(11)
Совокупность уравнений (1) – (4) и (9) – (11) образует основу электродинамики покоящихся сред.
Уравнения
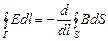 , (12)
, (12)
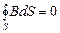 (13)
(13)
(первая пара) и
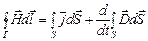 , (14)
, (14)
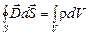 (15)
(15)
(вторая пара) представляют собой уравнения Максвелла в интегральной форме.
Переменное электрическое поле порождает магнитное, которое тоже оказывается переменным. Это переменное магнитное поле порождает электрическое и т.д. Таким образом, если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то в окружающем заряды пространстве возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке. Этот процесс будет периодическим во времени и пространстве и, следовательно, представляет собой волну.
Существование электромагнитных волн вытекает из уравнений Максвелла. В случае однородной нейтральной ( 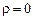 ) непроводящей (
) непроводящей ( 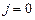 ) среды с постоянными проницаемостями
) среды с постоянными проницаемостями 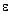 и
и 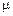
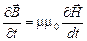 ,
, 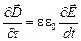 ,
,
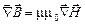 ,
, 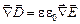 .
.
Поэтому уравнения (1) – (4) можно написать следующим образом:
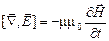 , (16)
, (16)
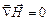 , (17)
, (17)
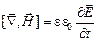 , (18)
, (18)
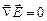 . (19)
. (19)
Возьмем ротор обеих частей уравнения (16):
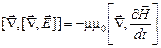 . (20)
. (20)
Изменение последовательности дифференцирования по координатам и времени приводит к равенству
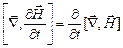 .
.
Произведя в (20) такую замену и подставив в получившееся уравнение значение (18) для ротора 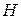 , получим
, получим
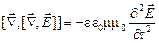 . (21)
. (21)
Так как 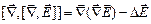 . В силу (19) первый член этого выражения равен нулю. Поэтому левая часть формулы (21) представляет собой
. В силу (19) первый член этого выражения равен нулю. Поэтому левая часть формулы (21) представляет собой 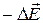 . Таким образом, опустив слева и справа знак минус, приходим к уравнению
. Таким образом, опустив слева и справа знак минус, приходим к уравнению
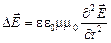 . (22)
. (22)
Так как 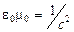 , то уравнению (22) можно придать вид
, то уравнению (22) можно придать вид
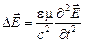 . (23)
. (23)
Раскрыв оператор Лапласа, получим
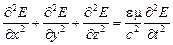 . (24)
. (24)
Взяв ротор обеих частей уравнения (18) и произведя аналогичные преобразования, придем к уравнению
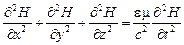 . (25)
. (25)
Уравнения (24) и (25) неразрывно связаны друг с другом, так как они получены из уравнений (16) и (18), каждое из которых содержит и 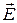 , и
, и 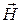 .
.
Уравнения (24) и (25) представляют собой типичные волновые уравнения. Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при производной по времени, дает фазовую скорость этой волны. Следовательно, уравнения (24) и (25) указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна
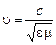 .
.
В вакууме (т.е. при 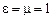 ) скорость электромагнитных волн совпадает со скоростью света.
) скорость электромагнитных волн совпадает со скоростью света.
Рассмотрим плоскую электромагнитную волну, распространяющуюся в нейтральной среде с постоянными проницаемостями 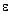 и
и 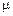 (
( 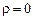 ,
, 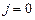 ,
, 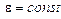 ,
, 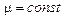 ). Направим ось
). Направим ось 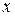 перпендикулярно к волновым поверхностям. Тогда
перпендикулярно к волновым поверхностям. Тогда 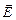 и
и 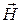 , а значит, и их компоненты по координатным осям не будут зависеть от координат
, а значит, и их компоненты по координатным осям не будут зависеть от координат 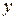 и
и 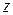 . Поэтому уравнения (5) – (8) упрощаются следующим образом:
. Поэтому уравнения (5) – (8) упрощаются следующим образом:
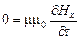 ,
, 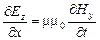 ,
, 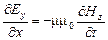 , (26)
, (26)
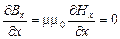 , (27)
, (27)
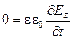 ,
, 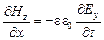 ,
, 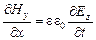 , (28)
, (28)
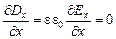 . (29)
. (29)
Уравнение (29) и первое из уравнений (28) показывают, что 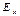 не может зависеть ни от
не может зависеть ни от 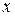 , ни от
, ни от 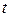 . Уравнение (27) и первое из уравнений (26) дают такой же результат для
. Уравнение (27) и первое из уравнений (26) дают такой же результат для 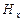 . Следовательно, отличные от нуля
. Следовательно, отличные от нуля 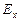 и
и 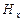 могут быть обусловлены лишь постоянными однородными полями, накладывающимися на электромагнитное поле волны. Само поле волны не имеет составляющих вдоль оси
могут быть обусловлены лишь постоянными однородными полями, накладывающимися на электромагнитное поле волны. Само поле волны не имеет составляющих вдоль оси 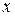 . Отсюда вытекает, что векторы
. Отсюда вытекает, что векторы 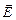 и
и 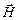 перпендикулярны к направлению распространения волны, т.е. что электромагнитные волны поперечны. В дальнейшем мы будем предполагать постоянные поля отсутствующими и полагать
перпендикулярны к направлению распространения волны, т.е. что электромагнитные волны поперечны. В дальнейшем мы будем предполагать постоянные поля отсутствующими и полагать 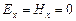 .
.
Два последних уравнения (26) и два последних уравнения (28) можно объединить в две независимые группы:
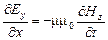 ,
, 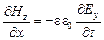 , (30)
, (30)
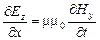 ,
, 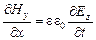 . (31)
. (31)
Первая группа уравнений связывает компоненты 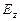 и
и 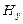 . Допустим, что первоначально было создано переменное электрическое поле
. Допустим, что первоначально было создано переменное электрическое поле 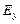 , направленное вдоль оси
, направленное вдоль оси 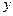 . Согласно второму из уравнений (30), это поле создаст магнитное поле
. Согласно второму из уравнений (30), это поле создаст магнитное поле 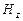 , направленное вдоль оси
, направленное вдоль оси 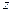 . В соответствии с первым уравнением (30), поле
. В соответствии с первым уравнением (30), поле 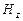 создаст электрическое поле
создаст электрическое поле 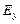 , и т.д. Ни поле
, и т.д. Ни поле 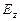 , ни поле
, ни поле 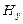 при этом не возникают. Аналогично, если первоначально было создано поле
при этом не возникают. Аналогично, если первоначально было создано поле 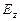 , то согласно уравнениям (31) появится поле
, то согласно уравнениям (31) появится поле 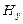 , которое возбудит поле
, которое возбудит поле 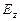 , и т.д. В этом случае не возникают поля
, и т.д. В этом случае не возникают поля 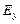 и
и 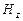 . Таким образом, для описания плоской электромагнитной волны достаточно взять одну из систем уравнений (30) или (31), положив компоненты, фигурирующие в другой системе, равными нулю.
. Таким образом, для описания плоской электромагнитной волны достаточно взять одну из систем уравнений (30) или (31), положив компоненты, фигурирующие в другой системе, равными нулю.
Возьмем для описания волны уравнения (30), положив 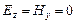 . Продифференцируем первое уравнение по
. Продифференцируем первое уравнение по 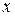 и произведем замену
и произведем замену 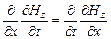 . Подставив
. Подставив 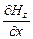 из второго уравнения, получим волновое уравнение для
из второго уравнения, получим волновое уравнение для 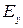 :
:
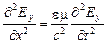 (32)
(32)
(мы заменили 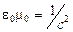 ). Продифференцировав по
). Продифференцировав по 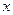 второе из уравнений (30), найдем после аналогичных преобразований волновое уравнение для
второе из уравнений (30), найдем после аналогичных преобразований волновое уравнение для 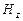 :
:
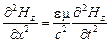 . (33)
. (33)
Полученные уравнения представляют собой частный случай уравнений (24) и (25).
Заметим, что 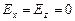 и
и 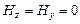 , так что
, так что 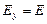 и
и 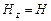 . Мы сохранили в уравнениях (32) и (33) индексы
. Мы сохранили в уравнениях (32) и (33) индексы 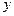 и
и 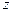 при
при 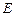 и
и 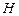 , чтобы подчеркнуть то обстоятельство, что векторы
, чтобы подчеркнуть то обстоятельство, что векторы 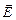 и
и 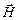 направлены вдоль взаимно перпендикулярных осей
направлены вдоль взаимно перпендикулярных осей 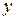 и
и 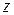 .
.
Простейшим решение уравнения (32) является функция
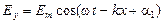 . (34)
. (34)
Решение уравнения (33) имеет аналогичный вид:
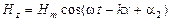 . (35)
. (35)
В этих формулах 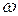 – частота волны,
– частота волны, 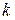 – волновое число, равное
– волновое число, равное 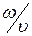 ,
, 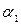 и
и 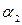 – начальные фазы колебаний в точках с координатой
– начальные фазы колебаний в точках с координатой 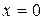 .
.
Подставим функции (34) и (35) в уравнения (30):
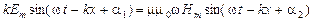 ,
,
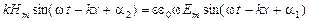 .
.
Для того чтобы уравнения удовлетворялись, необходимо равенство начальных фаз 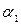 и
и 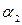 . Кроме того, должны выполнятся соотношения
. Кроме того, должны выполнятся соотношения
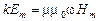 ,
, 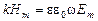 .
.
Перемножив эти два равенства, найдем, что
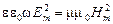 . (36)
. (36)
Таким образом, колебания электрического и магнитного векторов в электромагнитной волне происходят с одинаковой фазой ( 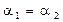 ), а амплитуды этих векторов связаны соотношением
), а амплитуды этих векторов связаны соотношением
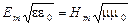 . (37)
. (37)
Для волны, распространяющейся в вакууме,
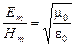 . (38)
. (38)
Умножив уравнение (34) на орт оси  (
(  ), а уравнение (35) на орт оси
), а уравнение (35) на орт оси 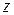 (
( 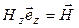 ), получим уравнения плоской электромагнитной волны в векторном виде:
), получим уравнения плоской электромагнитной волны в векторном виде:
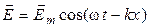 ,
, 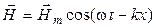 (39)
(39)
(мы положили 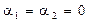 ).
).
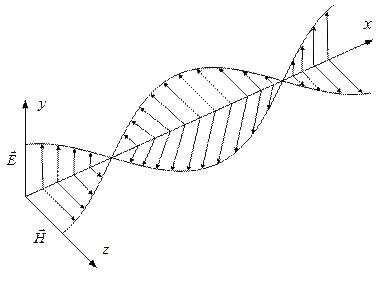
Рис. 1. Плоская электромагнитная волна.
На рис.1 показана «моментальная фотография» плоской электромагнитной волны. Из рисунка видно, что векторы 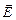 и
и 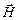 образуют с направлением распространения волны правовинтовую систему. В фиксированной точке пространства векторы
образуют с направлением распространения волны правовинтовую систему. В фиксированной точке пространства векторы 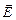 и
и 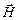 изменяются со временем по гармоническому закону. Они одновременно увеличиваются от нуля, затем через
изменяются со временем по гармоническому закону. Они одновременно увеличиваются от нуля, затем через 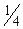 периода достигают наибольшего значения, причем, если
периода достигают наибольшего значения, причем, если 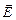 направлен вверх, то
направлен вверх, то 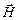 направлен вправо. Еще через
направлен вправо. Еще через 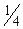 периода оба вектора одновременно обращаются в нуль. Затем опять достигают наибольшего значения, но на этот раз
периода оба вектора одновременно обращаются в нуль. Затем опять достигают наибольшего значения, но на этот раз 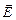 направлен вниз, а
направлен вниз, а 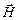 влево. И, наконец, по завершении периода колебания векторы снова обращаются в нуль. Такие изменения векторов
влево. И, наконец, по завершении периода колебания векторы снова обращаются в нуль. Такие изменения векторов 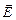 и
и 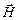 происходят во всех точках пространства, но со сдвигом по фазе, определяемым расстоянием между точками, отсчитанными вдоль оси
происходят во всех точках пространства, но со сдвигом по фазе, определяемым расстоянием между точками, отсчитанными вдоль оси 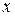 .
.
Дата добавления: 2015-12-16; просмотров: 1171;
