Построение автомата по блок-схеме алгоритма.
Существует класс конечных автоматов, который называют микропрограммными автоматами. На вход такого автомата поступают некоторые логические условия из множества 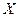 . Автомат вырабатывает микрокоманды, состоящие из микроопераций
. Автомат вырабатывает микрокоманды, состоящие из микроопераций 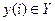 . Микрокоманда – это набор микроопераций. Последовательность выполнения микрокоманд, в зависимости от логических условий, задается блок-схемой алгоритма. Блок-схема алгоритма фактически определяет функцию переходов. Совокупность микрокоманд и функций переходов образуют микропрограмму.
. Микрокоманда – это набор микроопераций. Последовательность выполнения микрокоманд, в зависимости от логических условий, задается блок-схемой алгоритма. Блок-схема алгоритма фактически определяет функцию переходов. Совокупность микрокоманд и функций переходов образуют микропрограмму.
Блок-схема алгоритма или граф-схема алгоритма (ГСА) состоит из четырех типов вершин: 1-я начальная, 2-я конечная, 3-я операторная, 4-я условная.
Построение автомата по блок-схеме алгоритма происходит в два этапа:
1. производится определение числа состояний путем разметки и отметки граф-схемы;
2. определение графа автомата.
Символом 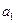 помечают вход вершины, следующей за начальным оператором в ГСА и вход конечной вершины (Рисунок 6). Символами
помечают вход вершины, следующей за начальным оператором в ГСА и вход конечной вершины (Рисунок 6). Символами 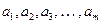 отмечаются входы в вершины, следующие за операторными вершинами (Рисунок 7).
отмечаются входы в вершины, следующие за операторными вершинами (Рисунок 7).

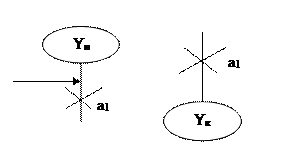
Рисунок 6
Рисунок 7
Если в результате разметки оказалось, что в одну и ту же вершину граф-схемы входят несколько размеченных стрелок, то им присваивается один и тот же символ. В дальнейшем символ 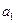 рассматривается как начальное состояние автомата, а символы
рассматривается как начальное состояние автомата, а символы 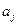 – как промежуточные состояния автомата. Т. о., число состояний автомата определяется числом различающихся символов
– как промежуточные состояния автомата. Т. о., число состояний автомата определяется числом различающихся символов 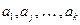 .
.
Построение микропрограммного автомата Мили по блок-схеме алгоритма состоит из двух этапов:
1. получение схемы ГСА;
2. построение графа переходов автомата.
Построение графа состояний автомата Мили по блок-схеме алгоритма:
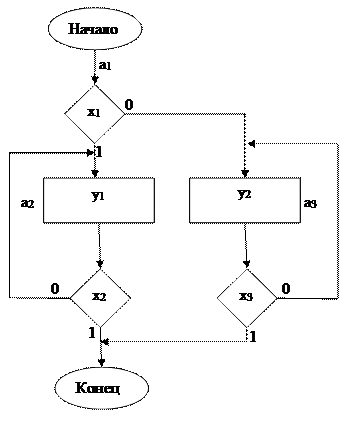
Для построения графа переходов по блок-схеме алгоритма находят пути переходов:
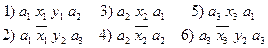

Построение микропрограммного автомата Мура по блок-схеме алгоритма состоит из двух этапов:
1. построение отмеченной ГСА;
2. построение графа переходов автомата (диаграммы Мура).
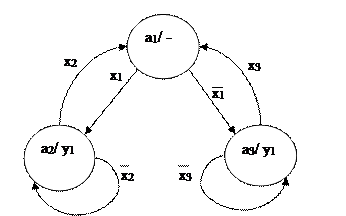
Построение графа состояний автомата Мура по блок-схеме алгоритма:
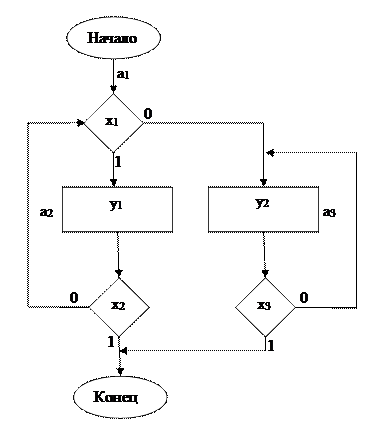
Для построения графа переходов по блок-схеме алгоритма находят пути переходов:
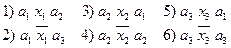
Дата добавления: 2015-12-16; просмотров: 5321;
