Автоматы Мили и Мура.
Понятие автомата. Автоматы Мили и Мура, их описание с помощью графов состояний. Построение автомата по блок-схеме алгоритма.
Теория автоматов представляет собой раздел дискретной математики, изучающий модели, преобразователи дискретной информации. Такими преобразователями являются как реальные устройства: компьютеры, живые организмы; так и воображаемые устройства: аксиоматические теории, математические машины.
Абстрактный автомат – это математическая модель, описывающая техническое устройство совокупностью входных, выходных сигналов и состояний.
Для описания автомата используют так называемую «шестёрку»:  , где:
, где:
множество 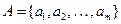 – множество состояний;
– множество состояний;
множество 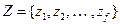 – множество входных символов;
– множество входных символов;
множество 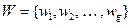 – множество выходных символов;
– множество выходных символов;
функция 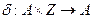 – функция переходов;
– функция переходов;
функция 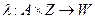 – функция выходов;
– функция выходов;
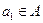 – начальное состояние автомата.
– начальное состояние автомата.

Рисунок 1 – Абстрактный автомат
Автоматы Мили и Мура.
В зависимости от способа определения выходного сигнала в синхронных автоматах различают:
1. Автомат первого рода, который называют автоматом Мили:
Автомат Мили задан системой канонических уравнений:
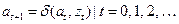 ,
,
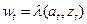 .
.

Рисунок 2 – Функциональная схема автомата Мили
2. Автомат второго рода, который называют автоматом Мура:
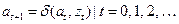 ,
,
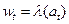 ,
,
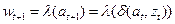 .
.

Рисунок 3 – Функциональная схема автомата Мура
Для задания конечного автомата 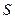 требуется описать все элементы множества
требуется описать все элементы множества  . Наиболее часто используемыми формами описания элементов множества
. Наиболее часто используемыми формами описания элементов множества 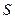 являются:
являются:
1. Табличный способ;
2. Графический способ;
3. Матричный способ.
Табличная форма автомата Мили иллюстрируется в таблице:
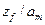
| 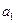
| 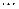
| 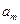
|
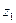
| 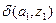
| 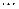
| 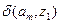
|
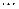
| 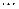
| 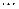
| 
|

| 
| 
| 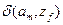
|
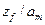
| 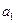
| 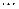
| 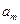
|
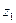
| 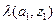
| 
| 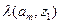
|
| 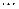
| 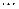
| 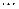
|

| 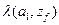
| 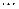
| 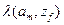
|
Автомат называется частично заданным, если он определен не для всех пар переходов 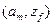 . Для такого автомата на месте отсутствующего перехода ставится прочерк, как в таблице переходов, так и в таблице выходов.
. Для такого автомата на месте отсутствующего перехода ставится прочерк, как в таблице переходов, так и в таблице выходов.
Графовая форма автомата:  представляется графом, в котором:
представляется графом, в котором:
- множество 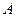 изображено вершинами графа;
изображено вершинами графа;
- функция 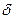 задана дугами графа, причем две вершины графа
задана дугами графа, причем две вершины графа 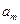 и
и 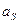 соединяются дугой, если в автомате существует переход из
соединяются дугой, если в автомате существует переход из 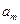 в
в 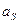 ;
;
- множество  изображено метками дуг:
изображено метками дуг:  ставится на дуге из вершины
ставится на дуге из вершины 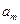 в вершину
в вершину 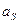 , если в автомате существует переход из
, если в автомате существует переход из 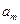 в
в 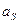 под действием выходного сигнала
под действием выходного сигнала  ;
;
- функция 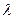 задана метками дуг (автомат Мили) или метками вершин (автомат Мура).
задана метками дуг (автомат Мили) или метками вершин (автомат Мура).
Для автомата Мили дуга из вершины 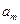 в вершину
в вершину 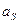 помечается выходным сигналом
помечается выходным сигналом 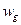 , если в автомате существует переход из
, если в автомате существует переход из 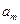 в
в 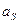 и при этом вырабатывается выходной сигнал
и при этом вырабатывается выходной сигнал 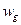 .
.
Для автомата Мура выходным сигналом 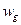 помечается вершина, определяющая
помечается вершина, определяющая 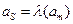 .
.
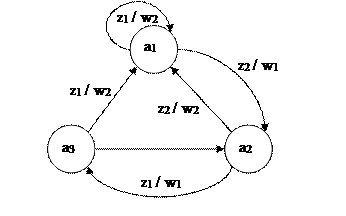
Рисунок 4 – Автомат Мили
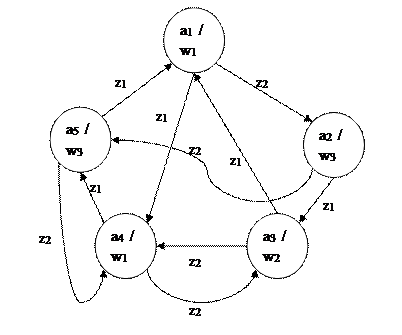
Рисунок 5 –Автомата Мура
Дата добавления: 2015-12-16; просмотров: 8234;
